1 Lösung 1c
Aufgabenstellung
Eine erste Modellierung des Querschnitts der Tunnelwand verwendet die Funktion mit Definitionsbereich
Zeigen Sie, dass die Bedingungen I und II in diesem Modell erfüllt sind. Berechnen Sie die Größe des spitzen Winkels, unter dem bei dieser Modellierung die linke Tunnelwand auf den Tunnelboden trifft. (6 BE)
Die Schülerinnen und Schüler untersuchen nun den Abstand der Graphenpunkte vom Ursprung des Koordinatensystems.
Zeigen Sie, dass gilt. (3 BE)
Es gibt Punkte des Querschnitts der Tunnelwand, deren Abstand zu M minimal ist. Bestimmen Sie die x-Koordinaten der Punkte , für die minimal ist, und geben Sie davon ausgehend diesen minimalen Abstand an. (5 BE)
Lösung
Es handelt sich um ein Extremwertproblem. Berechne daher die erste Ableitung.
Finde die Extremstellen, indem du die Ableitung gleich setzt.
Der Satz vom Nullprodukt besagt, dass man die einzelnen Faktoren setzen darf, um nach aufzulösen.
Nun setzt man die erhaltenen -Werte der Extremstellen in die Funktion ein, um die zugehörigen Abstände zu erhalten und damit außerdem festzustellen, wo es sich um Minima handelt.
Damit sieht man, dass die Werte für und kleiner sind als der von . Damit sind die minimalen Abstände an den Stellen und und betragen ca. .
2 Aufgabe 2 - Aufgabenstellung
Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ mit und Definitionsbereich , bei der offensichtlich Bedingung II erfüllt ist.
Bestimmen Sie c so, dass auch Bedingung I erfüllt ist, und berechnen Sie damit den Inhalt der Querschnittsfläche des Tunnels. (5 BE)
(zur Kontrolle: , Inhalt der Querschnittsfläche: )
Zeigen Sie, dass Bedingung III weder bei einer Modellierung mit p aus Aufgabe 1 noch bei einer Modellierung mit k erfüllt ist. (2 BE)
3 Lösung 2a
Aufgabenstellung
Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ mit und Definitionsbereich , bei der offensichtlich Bedingung II erfüllt ist.
Bestimmen Sie c so, dass auch Bedingung I erfüllt ist, und berechnen Sie damit den Inhalt der Querschnittsfläche des Tunnels. (5 BE)
(zur Kontrolle: , Inhalt der Querschnittsfläche: )
Aufgabenstellung
Bestimmung der Variable c
Die Bedingung I besagt, dass die Breite des Tunnels betragen soll. Das heißt, der Abstand zwischen der Nullstelle links und rechts vom Ursprung muss auch betragen und der Abstand einer der Nullstellen zum Ursprung genau .
Der Kosinus besitzt seine erste Nullstelle bei . Also setzt man das "Innere" des Kosinus gleich .
Man erhält also das Kontrollergebnis für .
Flächeninhalt der Querschnittsfläche
Wegen Bedingung I weiß man, dass die Nullstellen bei und sind. Für die Fläche muss man die Funktion von der ersten bis zur zweiten Nullstelle integrieren.
Damit hat man das Kontrollergebnis erhalten.
4 Lösung 2b
Aufgabenstellung
Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ mit und Definitionsbereich , bei der offensichtlich Bedingung II erfüllt ist.
Bestimmen Sie c so, dass auch Bedingung I erfüllt ist, und berechnen Sie damit den Inhalt der Querschnittsfläche des Tunnels. (5 BE)
(zur Kontrolle: , Inhalt der Querschnittsfläche: )
Zeigen Sie, dass Bedingung III weder bei einer Modellierung mit p aus Aufgabe 1 noch bei einer Modellierung mit k erfüllt ist. (2 BE)
Lösung
Bedingung III ist bei p nicht erfüllt
und Bedingung III: Der Tunnel ist auf einer Breite von mindestens 6 m mindestens 4 m hoch.
Das heißt, die Funktion müsste an der Stelle noch mindestens hoch sein. Das testet man, indem man in die Funktion einsetzt.
Man sieht, dass die Bedingung nicht erfüllt ist.
Bedingung III ist bei k nicht erfüllt
Man geht genauso vor wie für p.
Man sieht, dass auch hier die Bedinung nicht erfüllt wird.
5 Aufgabe 3 - Aufgabenstellung
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
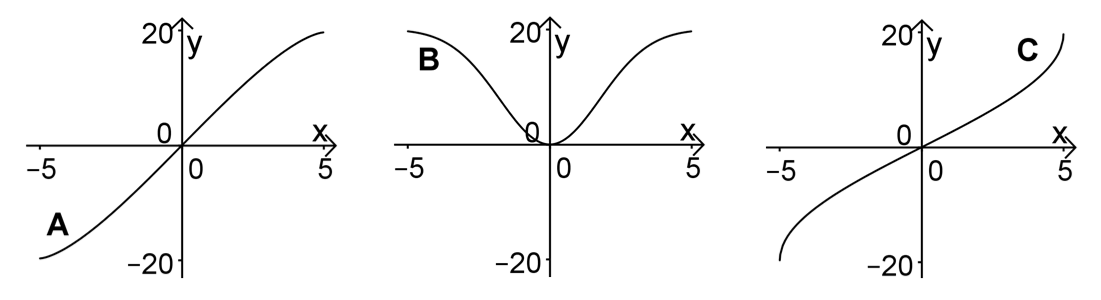
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt. Einer der Graphen A, B und C ist der Graph von F. Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)
Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit von dem in Aufgabe 2a berechneten Wert abweicht. (2 BE)
Der Tunnel soll durch einen Berg führen. Im betrachteten Querschnitt wird das Profil des Berghangs über dem Tunnel durch eine Gerade g mit der Gleichung modelliert.
Zeigen Sie, dass die Tangente an den Graphen von im Punkt parallel zu verläuft. Zeichnen Sie und in das Koordinatensystem aus Aufgabe 3a ein. (4 BE)
Der Punkt aus Aufgabe 3d entspricht demjenigen Punkt der Tunnelwand, der im betrachteten Querschnitt vom Hangprofil den kleinsten Abstand in Metern hat. Beschreiben Sie die wesentlichen Schritte eines Verfahrens zur rechnerischen Ermittlung von . (3 BE)
6 Lösung 3a
Aufgabenstellung
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Lösung
Jeder Punkt hat den Abstand zur Bodenmitte
Den Abstand kann man ähnlich wie bei 1b über den Satz des Pythagoras berechnen.
Damit hat man ausgerechnet, dass der Abstand von Punkt zur Bodenmitte immer beträgt.
Graph in Koordinatensystem zeichnen
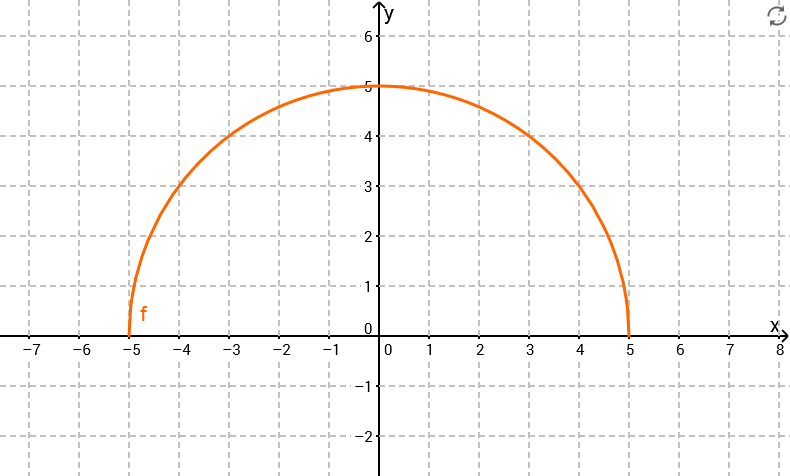
Bedingung III ist erfüllt
Gehe dazu vor wie bei Aufgabe 2b.
Die Funktion ist, wie man an dem Graphen sieht, punktsymmetrisch. An der Stelle ist noch mind. hoch, damit auch an der Stelle und erfüllt damit die Bedingung III.
7 Lösung 3b
Aufgabenstellung
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
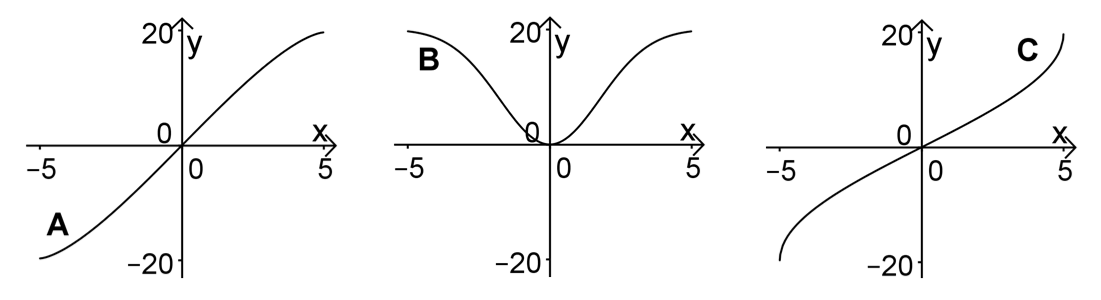
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt. Einer der Graphen A, B und C ist der Graph von F. Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)
Lösung
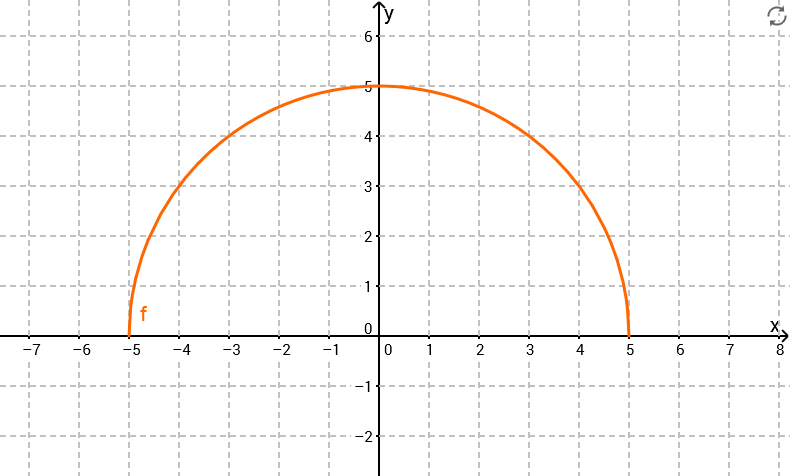
Überlege dir zuerst, wofür steht
steht also für die Fläche unter dem Graphen von bis . Wie man an dem Graphen von 3a sehen kann, handelt es sich dabei um einen Viertelkreis mit Radius . Berechne den Flächeninhalt.
Damit ist das Kontrollergebnis bestätigt.
Auswahl des richtigen Graphen
Man könnte sich zuerst überlegen, ob die Funktion links des Ursprungs positiv oder negativ sein muss.
Sie muss negativ sein, weil die Fläche zwar oberhalb der -Achse ist, aber man in negative Richtung integriert. Damit scheidet der Graph B aus, weil hier die Funktion links des Ursprungs positiv ist.
Also kommen nur noch die Graphen A und C in Frage. Bei Graph A ist der Flächenzuwachs erst groß und wird dann abgeschwächt, bei Graph C ist es umgekehrt. Überlege, was zutrifft.
Bei einem Kreis ist die Fläche um den Ursprung mehr als am Rand (siehe Graph 3a), das heißt, dass der Flächenzuwachs am Anfang groß ist und dann abnimmt.
Damit ist Graph A richtig und Graph C falsch.
8 Lösung 3c
Aufgabenstellung
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt. Einer der Graphen A, B und C ist der Graph von F. Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)
Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit von dem in Aufgabe 2a berechneten Wert abweicht. (2 BE)
Lösung
Fläche aus 2a: Fläche bei Modellierung mit :
Die Abweichung in Prozent berechnet man, indem man die Differenz der Werte durch den "ursprünglichen" Wert (also den der Aufgabe 2a) teilt.
Die Abweichung beträgt also ca.
9 Lösung 3d
Aufgabenstellung
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt. Einer der Graphen A, B und C ist der Graph von F. Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)
Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit von dem in Aufgabe 2a berechneten Wert abweicht. (2 BE)
Der Tunnel soll durch einen Berg führen. Im betrachteten Querschnitt wird das Profil des Berghangs über dem Tunnel durch eine Gerade g mit der Gleichung modelliert.
Zeigen Sie, dass die Tangente an den Graphen von im Punkt parallel zu verläuft. Zeichnen Sie und in das Koordinatensystem aus Aufgabe 3a ein. (4 BE)
Lösung
Tangente verläuft parallel zu
Um Parallelität zu prüfen, muss man die Steigung der Tangente berechnen. Dazu bildet man die erste Ableitung und setzt ein.
Die Steigungen von und stimmen also überein, also sind sie parallel.
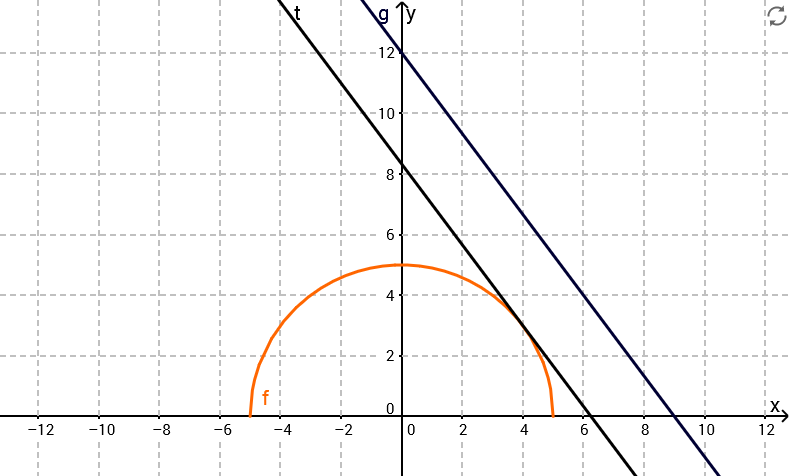
Einzeichnen von und
Dazu benötigt man die Geradengleichung von . Berechne dazu erst den Punkt .
Der Punkt hat also die Koordinaten . Setze diese in die Geradengleichung ein und berechne den -Achsenabschnitt von .
Die Geradengleichung von ist also . Mit diesen Infos kannst du die Geraden einzeichnen.
10 Lösung 3e
Aufgabenstellung
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt. Einer der Graphen A, B und C ist der Graph von F. Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)
Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit von dem in Aufgabe 2a berechneten Wert abweicht. (2 BE)
Der Tunnel soll durch einen Berg führen. Im betrachteten Querschnitt wird das Profil des Berghangs über dem Tunnel durch eine Gerade g mit der Gleichung modelliert.
Zeigen Sie, dass die Tangente an den Graphen von im Punkt parallel zu verläuft. Zeichnen Sie und in das Koordinatensystem aus Aufgabe 3a ein. (4 BE)
Der Punkt aus Aufgabe 3d entspricht demjenigen Punkt der Tunnelwand, der im betrachteten Querschnitt vom Hangprofil den kleinsten Abstand in Metern hat. Beschreiben Sie die wesentlichen Schritte eines Verfahrens zur rechnerischen Ermittlung von . (3 BE)
Lösung
Für den kleinsten Abstand braucht man die Lotgerade von R auf g. Die Steigung ist die Normalensteigung und wird mit Hilfe der Formel berechnet. Dann setzt man den Punkt ein und berechnet den -Achsenabschnitt. Damit hat man die Lotgerade. Nun muss man den Schnittpunkt der Lotgerade mit berechnen. Als Letztes berchnet man den Abstand von dem Schnittpunkt zu .
