Aufgaben zur Hinführung auf schwierige Extremwertprobleme

Beweise, dass in jedem Dreieck der größmögliche Inhalt einbeschreibbarer Rechtecke gleich der halben Dreiecksfläche ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertproblem

Bei dieser Aufgabe geht es um die Extremwerte von in Dreiecken einbeschriebenen Rechtecken.

Es ist nachzuweisen, dass alle in ein Dreieck einbeschreibbaren Rechtecke den gleichen maximalen Inhalt, nämlich die halbe Dreiecksfläche haben.

Mache dir zunächst eine anschauliche Vorstellung von der Bedeutung der Behauptung, indem du im nachfolgenden Applet die 6 Gleiterpunkte $P_{1}$ , . . . , $P_{6}$ verschiebst.

Du verstehst dabei auch, wie und wo in den verschiedenen Dreiecksformen - spitzwinklig, rechteckig, stumpfwinklig - Rechtecke einbeschrieben werden können.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/KXDnGWsb]

Beweis der Behauptung

Dem Applet entnimmst du anschaulich:

Jedes der von den Punkten $P_{1}$ bis $P_{6}$ ausgehende einbeschriebene Rechteck liegt mit einer Rechtecksseite auf einer Dreiecksseite. Die Längen der Rechtecksseiten seien $x L E$ und $y L E$ .

Jedes Rechteck erzeugt eine Strahlensatzfigur.

Die Zielfunktion eines jeden Rechtecks für seinen maximalen Inhalt lautet:

$A (x; y) = x \cdot y$ ,

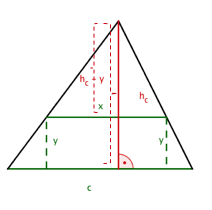
Die Nebenbedingung ergibt sich aus dem Strahlensatz. Wende diesen an.

Mit dem Strahlensatz gilt:

$\frac{x}{c} = \frac{h_{c} - y}{h_{c}}$

wobei $c$ eine beliebige Dreiecksseite und $h_{c}$ die zugehörige Dreieckshöhe ist.

Löse die Gleichung nach $y$ auf.

$\begin{array}{rcll} \frac{x}{c} & = & \frac{h_{c} - y}{h_{c}} & | \cdot h_{c} \\ \frac{h_{c}}{c} \cdot x & = & h_{c} - y \\ y & = & - \frac{h_{c}}{c} \cdot x + h_{c} \end{array}$

Setze $y$ in $A (x; y)$ ein.

$A (x) = x \cdot (- \frac{h_{c}}{c} \cdot x + h_{c})$

$A (x) = - \frac{h_{c}}{c} \cdot x^{2} + h_{c} \cdot x$

Bilde $A^{'} (x)$ .

$A^{'} (x) = - \frac{2 h_{c}}{c} + h_{c}$

Setze $A^{'} (x)$ gleich Null.

$\begin{array}{rcl} - \frac{2 h_{c}}{c} \cdot x + h_{c} & = 0 \\ x & = \frac{c}{2} \end{array}$

Überzeuge dich, dass $A^{''} (\frac{c}{2})$ negativ ist. Dann ergibt sich ein maximaler Flächeninhalt.

$A^{''} (x) = - \frac{h_{c}}{c} < 0 für jedes x$

Setze $x = \frac{c}{2}$ in die Nebenbedingung ein, um auch die 2. Rechtecksseite zu erhalten.

$y = - \frac{h_{c}}{c} \cdot \frac{c}{2} + h_{c} \Rightarrow$

$y = \frac{h_{c}}{2}$

Setze $x = \frac{c}{2}$ und $y = \frac{h_{c}}{2}$ in die Zielfunktion $A (x; y)$ ein.

$A (x; y) = \frac{c}{2} \cdot \frac{h_{c}}{2}$

$A (x; y) = \frac{1}{4} \cdot c \cdot h_{c}$

Vergleiche die berechnete maximale Rechtecksfläche mit der Dreiecksfläche.

$A_{m a x . R e c h t e c k} = \frac{1}{4} c \cdot h_{c} = \frac{1}{2} \cdot (\frac{1}{2} c \cdot h_{c}) = \frac{1}{2} \cdot A_{Dreieck}$

Ergebnis

Jedes in ein Dreieck einbeschriebene Rechteck liegt mit einer Seite auf einer Dreiecksseite. Die flächenmäßig größten einbeschreibbaren Rechtecke haben den Flächeninhalt "1/4 mal Grundlinienlänge mal zugehörige Höhe".

Damit sind sie - auch wenn sie über verschiedenen Dreiecksseiten errichtet worden sind - gleich groß und zwar gerade halb so groß wie die Dreiecksfläche.

Ergänzung

Da - außer in gleichschenklig rechtwinkligen Dreiecken - eine Dreiecksseite und ihre dazugehörige Höhe verschieden sind - können die maximalen einbeschriebenen Rechtecke - außer in gleichschenklig rechtwinkligen Dreiecken - keine Quadrate sein.

Lasse im nachfolgenden Applet durch eine geeignete Verschiebung des Gleiterpunktes $P$ solch einen Sonderfall einer einbeschriebenen Quadratfläche entstehen.

[https://www.geogebra.org/material/iframe/id/eXEcw9BS]

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?