Aufgaben zur Hinführung auf schwierige Extremwertprobleme

Hier findest du Aufgaben zu Extremwertproblemen. Lerne, dich in schwierige Extremwertproleme hineinzudenken und erweitere dein Verständnis.

Manche ebene geometrische Figuren werden alleine durch ihren Umfang oder alleine durch ihren Flächeninhalt bestimmt.

Einige ebene geometrische Formen sind umfangsstabil. Das heißt, flächengleiche Figuren solch einer Form haben auch gleichen Umfang.

Welche der folgenden Aussagen stimmt?
Klicke die Zutreffenden an!
- Je größer der Flächeninhalt eines Kreises, desto größer sein Umfang.
- Je größer der Flächeninhalt eines Quadrats, desto größer sein Umfang.
- Je größer der Flächeninhalt eines Dreiecks, desto größer sein Umfang.
Bei dieser Aufgabe geht es um den Zusammenhang von Umfang und Flächeninhalt bei Kreisen, bei Dreiecken und bei Quadraten.
Quadrate sind umfangsstabil:
Je größer der Umfang eines Quadrats, desto größer sein Flächeninhalt.
Genauer gilt mit der Quadratseite $a$ :
$\displaystyle U_{Q} =4\cdot a\quad \Rightarrow\quad a=\frac{U_{Q}}{4}\quad$ und somit:
$\displaystyle A_{Quadrat} = a^2\;=\left(\frac {U_{Q}}{4}\right)^2=\frac {1} {16}\cdot \left(U_{Q}\right) ^2$
Kreise sind umfangsstabil:
Je größer der Umfang eines Kreises, desto größer sein Flächeninhalt.
Genauer gilt mit dem Radius $r$ :
$\displaystyle U_{r}= 2r\pi\quad\Rightarrow\quad r= \frac {U_{r}}{2\pi}\quad$ und somit:
$\displaystyle A_{Kreis}= r^2\cdot \pi=\frac{1}{4\pi}\cdot\left(U_{r}\right)^2$
Dreiecke sind nicht umfangsstabil:
Vergleiche die Dreiecke in der nebenstehenden Grafik:
Wegen gleicher Grundlinie und gleicher Höhe haben alle fünf Dreiecke gleiche Fläche aber unterschiedliche Umfänge.
Ergänzung:
Gleichseitige Dreiecke sind umfangsgleiche geometrische Formen:
Bei gegebener Dreieckseite $a$ gilt:
$\displaystyle U_{gl.s.Dr.}=3\cdot a\quad \Rightarrow\quad a=\frac{U_{gl.s.Dr.}}{3}\quad$ und somit:
$\displaystyle A_{gl.s.Dr.}=\frac{\sqrt{3}}{4}\cdot a^2=\frac{\sqrt{3}}{36}\cdot \left(U_{gl.s.Dr.}\right)^2$
Ein vorgegebener Umfang bestimmt also den Flächeninhalt eines gleichseitigen Dreiecks eindeutig.
Die Behauptung "Je größer der Umfang eines Dreiecks, desto größer sein Flächeninhalt" gilt demnach nur für gleichseitige Dreiecke.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

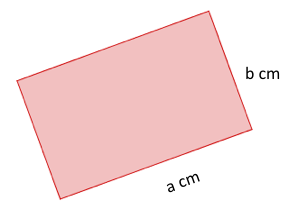
Zeige, dass ein Rechteck nicht formstabil ist:

Erzeuge zur Begründung im nebenstehenden Applet durch Verschieben des Reglers 5 weitere Rechtecke.

Worin stimmen alle 6 Rechtecke überein?

Worin unterscheiden sie sich?

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/e9wz6bpv]

Bei dieser Aufgabe entdeckst du, dass Rechtecke bei gleichem Umfang unterschiedliche Flächeninhalte haben können.

Die Maße der Rechtecke:

	a	b	Umfang	Fläche
Rechteck 1	0,3 LE	1,7 LE	4 LE	0,51 LE²
Rechteck 2	0,6 LE	1,4 LE	4 LE	0,84 LE²
Rechteck 3	0,9 LE	1,1 LE	4 LE	0,99 LE²
Rechteck 4	1,2 LE	0,8 LE	4 LE	0,96 LE²
Rechteck 5	1,5 LE	0,5 LE	4 LE	0,73 LE²
Rechteck 6	1,8 LE	0,2 LE	4 LE	0,36 LE²

Ergebnis:

Alle Rechtecke haben gleichen Umfang, aber unterschiedliche Flächeninhalte.

Dazu könnte man auch sagen, Rechtecke sind nicht formstabil.

Naheliegend ist dadurch die Überlegung:

Welche Rechtecksform liefert bei einem Rechtecksumfang von $4\,\text{LE}$ die größte Fläche?

Diese Extremwertaufgabe löst du in der nächsten Aufgabe.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

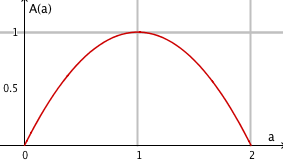
Ein Rechteck habe den Umfang $U=4\,\text{cm}$ . Berechne die Seitenlängen $a$ und $b$ so, dass das Rechteck den größtmöglichen Flächeninhalt $A$ besitzt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

In dieser Aufgabe bestimmst du das größtmögliche Rechteck durch die Ableitung oder alternativ durch die quadratische Ergänzung der Zielfunktion.

Der Umfang $U$ des Rechtecks beträgt $4\,\text{cm}$ bei den noch nicht bekannten Seitenlängen $a\,\text{cm}$ und $b\,\text{cm}$ .

Gesucht ist der größtmögliche Flächeninhalt $A$ des Rechtecks.

Die Formel für den Flächeninhalt eines Rechtecks ergibt deshalb die Zielfunktion.

Hinweis:

Haben bei Extremwertaufgaben die betrachteten Größen die gleiche Maßeinheit, begnügt man sich bei den verwendeten Funktionen meist auf die Angaben der jeweiligen Maßzahlen.

Zielfunktion:

$A(a;b)=a\cdot b$

Die Formel für den vorgegebenen Umfang ist die Nebenbedingung der Extremwertaufgabe

Nebenbedingung:

$U(a;b)=2\cdot a + 2\cdot b$

Setze in die Nebenbedingung für $U(a;b)$ den Wert 4 ein.

$2a+2b=4$

Löse die Gleichung nach $b$ auf. (Du könntest auch nach $a$ auflösen.)

$\Rightarrow\quad\; b=2-a$

Setze in der Zielfunktion für $b$ den Term $2-a$ an.

Beachte: $A$ wird dadurch zu einer Funktion der einen Varaiablen $a$ .

\displaystyle A\left(a\right)

=

\displaystyle a\cdot\left(2-a\right)

↓

Multipliziere die Klammer aus.

Für $a$ gilt: $a\in\,]0;2[$ .

\displaystyle A\left(a\right)

=

\displaystyle -a^2+2a

$\mathbb {D}_A=\;]0;2[$

Bilde die 1. Ableitung der Zielfunktion $A(a)$ .

$A'(a)=-2a+2$

Setze $A'(a)$ gleich Null und löse nach $a$ auf.

$\def\arraystretch{1.25} \begin{array}{rcl}-2a+2&=0\\a&=1\end{array}$

Überprüfe mit der 2. Ableitung, dass $a=1$ tatsächlich für die Zielfunktion ein Maximum ergibt.

$A''(a)=-2$

$A''(a)$ ist eine konstante Funktion. Somit ist auch $A''(1)=-2< 0$ und $a=1$ ergibt einen maximalen Flächeninhalt.

Setze $a=1$ in die Nebenbedingung ein, um auch die 2. Rechtecksseite $b$ zu erhalten.

$b=2-1=1$

Ergebnis:

Das Rechteck, das bei einem gegebenen Umfang von 4 $\,\text{cm}$ den größtmöglichen Flächeninhalt besitzt, ist ein Quadrat mit der Seitenlänge 1 $\,\text{cm}$ . Der gesuchte Flächeninhalt ist also $1\,\text{cm}^2$ .

Alternative Lösung

Der Graph der Zielfunktion $A(a)=-a^2+2a;\quad \mathbb{D}_A=]0;2[$ ist eine nach unten geöffnete Parabel. Ihr Maximum ist der Scheitelpunkt.

Diesen kann man durch eine quadratische Ergänzung ermitteln.

$\displaystyle A$	$=$	$\displaystyle -a^2+2a$
	↓	Klammere $-1$ aus.
	$=$	$\displaystyle -\left(a^2-2a\right)$
	↓	Ergänze quadratisch.
	$=$	$\displaystyle -(a^2-2a\color{red}{+1^2}\color{green}{-1^2})$
	↓	Fasse zur binomischen Formel zusammen.
	$=$	$\displaystyle -\left(a-1\right)^2+1$

Lies nun den Scheitelpunkt ab.

$\Rightarrow\quad S(1|1)$

Aus der Zielfunktion für $a=1$ kannst du den maximalen Flächeninhalt bestimmen.

$\Rightarrow \quad A_{max}=A(1)=-1^2+2\cdot 1= 1$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

2
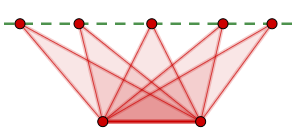
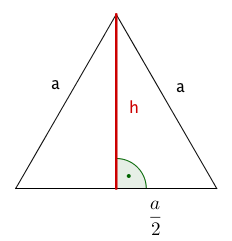
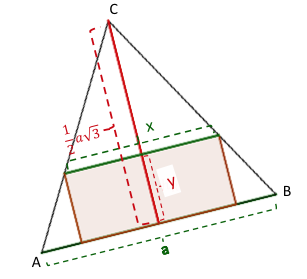
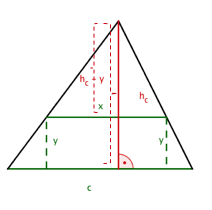
Gegeben sei ein gleichseitiges Dreieck mit der Seitenlänge $a\,\text{LE}$ .
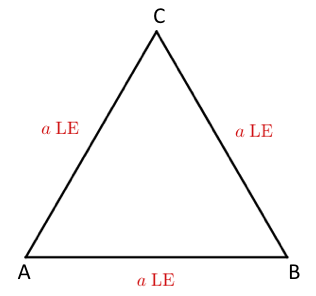
1. Auf welche Weise kann man dem Dreieck Rechtecke einbeschreiben?
  Klicke die richtige Antwort an.
  Dem Dreieck können Rechtecke so einbeschrieben werden, dass auf jeder der Dreiecksseiten eine Rechtecksseite liegt.
  Einem gleichseitigen Dreieck kann auf keine Weise ein Rechteck einbeschrieben werden.
  Dem Dreieck können Rechtecke nur so einbeschrieben werden, dass eine Rechtecksseite auf der Grundlinie $[AB]$ des Dreiecks liegt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: gleichseitiges Dreieck
  Einem Dreieck ein Rechteck "einbeschreiben" bedeutet, dass jeder Eckpunkt des Rechtecks auf einer Dreiecksseite liegt. Zwei Eckpunke des Rechtecks müssen dann auf derselben Dreiecksseite liegen. Dafür kommt jede Dreiecksseite in Frage.
  Also kann man einem gleichseitigen Dreieck auf dreifache Weise Rechtecke einbeschreiben.
  Verschiebe zur Veranschaulichung im gegebenen Applet die Gleiterpunkte $P_1$ , $P_2$ , $P_3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne den größtmöglichen Flächeninhalt eines Rechtecks, das dem Dreieck einbeschrieben werden kann.
  Wie viel Prozent der Dreiecksfläche besitzt solch ein maximales Rechteck?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  In dieser Aufgabe soll einem gleichseitigen Dreieck ein möglichst großes Rechteck einbeschrieben werden.
  Lösungsstrategie:
  Du berechnest als erstes die Höhe des gleichseitigen Dreiecks. Entweder mit Hilfe des Satzes des Pythagoras oder du entnimmst sie einer Formelsammlung.
  Dann kannst du - ohne Koordinatensystem - die Nebenbedingung der Extremwertaufgabe mit Hilfe des Strahlensatzes aufstellen.
  Höhe im gleichseitigen Dreieck (Pythagoras):
  $\def\arraystretch{1.25} \begin{array}{rcl}h^2+\left(\frac{a}{2}\right)^2&=&a^2\\h^2&=&a^2-\left(\frac{a}{2}\right)^2\\h^2&=&\frac 34a^2\\h&=&\frac a 2\sqrt 3\end{array}$
  Zielfunktion sei die Formel für den Flächeninhalt eines Rechtecks mit den Seitenlängen $x\,LE$ und $y\,LE$ :
  $A(x;y)=x\cdot y$
  Die Nebenbedingung für $x$ und $y$ ergibt sich aus dem Strahlensatz:
  $\displaystyle \frac {x} {a} = \frac {\frac{1}{2} a \sqrt{3}-y} {\frac{1}{2} a \sqrt{3}}$
  Löse die Gleichung nach $y$ auf.
  $\def\arraystretch{1.25} \begin{array}{rcll}\frac{x}{a}&=&\frac{\frac{1}{2} a \sqrt{3}-y}{\frac{1}{2} a \sqrt{3}}&|\cdot \frac{1}{2}a \sqrt{3}\\\frac{x}{2} \sqrt{3}&=&\frac{1}{2} a \sqrt{3}-y&|+y-\frac{x}{2}\ \sqrt{3}\\y&=&\frac{1}{2} \sqrt{3}\left(a-x\right)\end{array}$
  Setze $y$ in die Zielfunktion $A(x;y)=x \cdot y$ ein:
  $\def\arraystretch{1.25} \begin{array}{rcl} A(x)&=&x\cdot\frac{1}{2} \sqrt{3}(a-x)\\A(x)&=&-\frac{1}{2} \sqrt{3}\cdot x^2+\frac{1}{2}\sqrt{3}\cdot a\cdot x\end{array}$
  $\mathbb{D}_A=]0;a[$
  Bilde $A'(x)$ .
  $A'(x)=- \sqrt{3}\cdot x+\frac{1}{2} \sqrt{3}\cdot a$
  $A'(x)=\sqrt{3}(\frac 12a-x)$
  Setze $A'(x)$ gleich Null.
  $\def\arraystretch{1.25} \begin{array}{rrcl}&\sqrt{3}(\frac 12a-x)&=&0\\ \Rightarrow &x&=&\frac{1}{2}a\end{array}$
  Überprüfe, ob $A''(0{,}5a)$ negativ ist, damit sich ein Maximum ergibt.
  $A''(x)=- \sqrt{3}$
  Ergebnis:
  Die Breite des gesuchten flächengrößten Rechtecks ist gerade halb so groß wie die Seitenlänge des Dreiecks.
  Für die Höhe $y$ ergibt sich:
  $y=\frac 12 \sqrt{3}\cdot \frac12 a=\frac{a}{4}\sqrt{3}$
  Für die Fläche des gesuchten größten Rechtecks gilt:
  $\displaystyle A_{max}=\frac {a}{2}\cdot \frac{a}{4} \sqrt{3}= \frac{a^2}{8}\sqrt{3}$
  Der Flächeninhalt dieses Rechtecks ist gerade 50 Prozent der Dreiecksfläche, denn für diese gilt:
  $A_{Dreieck}= \frac 12 \cdot a\cdot \frac{a}{2} \sqrt{3}=\frac{a^2}{4} \sqrt {3}$ .
  Erweiterung der Aufgabenstellung:
  Aus der Punktsymmetrie eines gleichseitigen Dreiecks zu seinem Mittelpunkt folgt, dass alle drei einbeschreibbaren maximalen Rechtecke gleich groß sind.
  Im nachstehenden Applet kannst du dies grafisch nachvollziehen, indem du die verschiedenen Gleiterpunkte verschiebst.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Beschreibe einem gleichseitigen Dreieck (Seitenlänge $5\, cm$ ) drei verschiedene gleichgroße Rechtecke mit dem Inhalt von jeweils $4\,cm^2$ ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  In dieser Aufgabe sind die Flächeninhalte der einzubeschreibenden Rechtecke vorgegeben. Folgender Lösungsplan für die Konstruktion ist möglich:
  Über jeder Dreiecksseite kann es zwei verschiedene Rechtecke mit dem gleichen Inhalt von $4\,LE$ geben. Konstruiere also z.B. diese beiden über der Dreiecksseite $[AB]$ und ein drittes über der Dreiecksseite $[AC]$ .
  Bevor du konstruierst, musst du die Rechtecksseiten $x\,LE$ und $y\,LE$ berechnen. Benutze dazu eine Zielfunktion und die Nebenbedingung wie in der vorausgehenden Teilaufgabe b).
  Durchführung:
  Zielfunktion
  $A(x;y)=x\cdot y$
  Nebenbedingung
  $y=-\frac12 \sqrt{3}x+\frac 52 \sqrt{3}\;\Rightarrow$
  $y=\frac 12 \sqrt{3}\left(-x+5\right)$
  Setze in der Zielfunktion für $A(x;y)$ den Wert 4 und für y den Term der Nebenbedingung ein und ordne die entstehende quadratische Gleichung.
  $\def\arraystretch{1.25} \begin{array}{rcll}x\cdot\frac 12 \sqrt{3}(-x+5)&=&4&\\\frac 12 \sqrt{3}x^2-\frac 52 \sqrt{3}+4&=&0&|:\frac 12 \sqrt{3}\\x^2-5x+\frac {8}{\sqrt{3}}&=&0&\end{array}$
  Löse die Gleichung mit der Mitternachtsformel und runde die Ergebnisse.
  $x_1\approx{3{,}77}$
  $x_2\approx{1{,}22}$
  Berechne die zugehörigen y-Werte.
  $y_1\approx{\frac 12 \sqrt{3}(-3{,}77+5)}\approx{1{,}06}$
  $y_2\approx{\frac 12 \sqrt{3}(-1{,}22+5)} \approx3{,}27$
  Zur Konstruktion der Rechtecke benutzt du die berechneten y-Werte:
  Rechteck 1 über $[AB]$ :Zeichne eine Parallele zu $[AB]$ im Abstand 1,06. Schneide diese mit den Dreiecksseiten $[AC]$ und $[BC]$ und ergänze zum Rechteck.
  Analog erhältst du das Rechteck 2 über $[AB]$ durch eine Parallele im Abstand 3,27.
  Das Rechteck 3 über der Seite $[AC]$ erhältst du durch die Parallele im Abstand 1,06 zu $[AC]$ und die entsprechende Ergänzung zum Rechteck.
  Die einzelnen Konstruktionsschritte kannst du im folgenden Applet schrittweise nachvollziehen. Benutze dazu die untere Navigationsleiste.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Tipp: Berechne mit Hilfe des Strahlensatzes die Nebenbedingung für das Einbeschreiben von Rechtecken in ein gleichseitiges Dreieck (oder entnimm die Formel der vorangehenden Aufgabe). Berechne daraufhin aus der Flächenformel für das Rechteck mit der sich ergebenden quadratischen Gleichung die möglichen Seitenlängen.
  Runde die Ergebnisse auf ein sinnvolles Maß und konstruiere damit die gesuchten möglichen Rechtecke.
3
Beweise, dass in jedem Dreieck der größmögliche Inhalt einbeschreibbarer Rechtecke gleich der halben Dreiecksfläche ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertproblem
Bei dieser Aufgabe geht es um die Extremwerte von in Dreiecken einbeschriebenen Rechtecken.
Es ist nachzuweisen, dass alle in ein Dreieck einbeschreibbaren Rechtecke den gleichen maximalen Inhalt, nämlich die halbe Dreiecksfläche haben.
Mache dir zunächst eine anschauliche Vorstellung von der Bedeutung der Behauptung, indem du im nachfolgenden Applet die 6 Gleiterpunkte $P_1$ , . . . , $P_6$ verschiebst.
Du verstehst dabei auch, wie und wo in den verschiedenen Dreiecksformen - spitzwinklig, rechteckig, stumpfwinklig - Rechtecke einbeschrieben werden können.
Beweis der Behauptung
Dem Applet entnimmst du anschaulich:
Jedes der von den Punkten $P_1$ bis $P_6$ ausgehende einbeschriebene Rechteck liegt mit einer Rechtecksseite auf einer Dreiecksseite. Die Längen der Rechtecksseiten seien $x\,LE$ und $y\,LE$ .
Jedes Rechteck erzeugt eine Strahlensatzfigur.
Die Zielfunktion eines jeden Rechtecks für seinen maximalen Inhalt lautet:
$A(x;y)=x\cdot y$ ,
Die Nebenbedingung ergibt sich aus dem Strahlensatz. Wende diesen an.
Mit dem Strahlensatz gilt:
$\displaystyle \frac {x}{c}=\frac {h_c-y}{h_c}$
wobei $c$ eine beliebige Dreiecksseite und $h_c$ die zugehörige Dreieckshöhe ist.
Löse die Gleichung nach $y$ auf.
$\def\arraystretch{1.25} \begin{array}{rcll}\displaystyle \frac{x}{c}&=&\frac{h_c-y}{h_c}&|\cdot h_c\\\frac{h_c}{c}\cdot x&=&h_c-y\\y&=&-\frac{h_c}{c}\cdot x+h_c\end{array}$
Setze $y$ in $A(x;y)$ ein.
$A(x)=x\cdot (-\frac{h_c}{c}\cdot x+h_c)$
$A(x)=-\frac{h_c}{c}\cdot x^2+h_c\cdot x$
Bilde $A'(x)$ .
$A'(x)=-\frac{2h_c}{c}+h_c$
Setze $A'(x)$ gleich Null.
$\def\arraystretch{1.25} \begin{array}{rcl}-\frac{2h_c}{c}\cdot x + h_c&=0\\x&=\frac{c}{2}\end{array}$
Überzeuge dich, dass $A''(\frac{c}{2})$ negativ ist. Dann ergibt sich ein maximaler Flächeninhalt.
$A''(x)=-\frac{h_c}{c}<0 \,\text{für jedes}\, x$
Setze $x=\frac{c}{2}$ in die Nebenbedingung ein, um auch die 2. Rechtecksseite zu erhalten.
$y=-\frac{h_c}{c}\cdot \frac{c}{2}+h_c\quad\Rightarrow$
$y=\frac{h_c}{2}$
Setze $x=\frac{c}{2}$ und $y=\frac{h_c}{2}$ in die Zielfunktion $A(x;y)$ ein.
$A(x;y)=\frac{c}{2}\cdot \frac{h_c}{2}$
$A(x;y)=\frac14\cdot c \cdot h_c$
Vergleiche die berechnete maximale Rechtecksfläche mit der Dreiecksfläche.
$A_{max. Rechteck}=\frac14c \cdot h_c=\frac12\cdot (\frac12 c\cdot h_c)=\frac12 \cdot \,A_{\text{Dreieck}}$
Ergebnis
Jedes in ein Dreieck einbeschriebene Rechteck liegt mit einer Seite auf einer Dreiecksseite. Die flächenmäßig größten einbeschreibbaren Rechtecke haben den Flächeninhalt "1/4 mal Grundlinienlänge mal zugehörige Höhe".
Damit sind sie - auch wenn sie über verschiedenen Dreiecksseiten errichtet worden sind - gleich groß und zwar gerade halb so groß wie die Dreiecksfläche.
Ergänzung
Da - außer in gleichschenklig rechtwinkligen Dreiecken - eine Dreiecksseite und ihre dazugehörige Höhe verschieden sind - können die maximalen einbeschriebenen Rechtecke - außer in gleichschenklig rechtwinkligen Dreiecken - keine Quadrate sein.
Lasse im nachfolgenden Applet durch eine geeignete Verschiebung des Gleiterpunktes $P$ solch einen Sonderfall einer einbeschriebenen Quadratfläche entstehen.

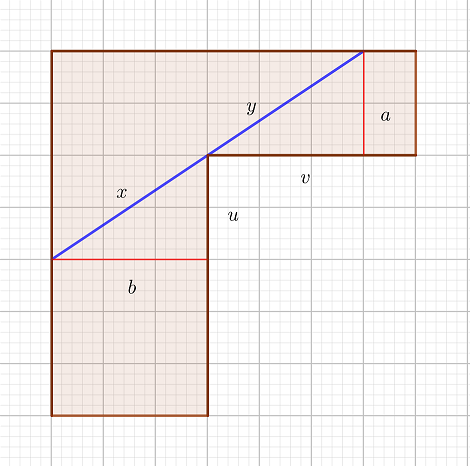
Das Problem kennt jeder Möbelpacker:

Wie breit kann ein Schrank höchstens sein, damit er - bei gegebener Länge und ohne angehoben zu werden - um eine Flurecke geschoben werden kann?

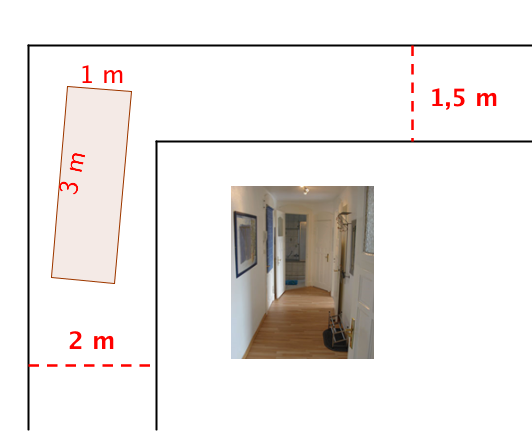
Du kannst bei dieser Aufgabe Argumentieren - Schätzen - Experimentieren - Rechnen.

Argumentieren - schätzen
Beschreibe, wie ein Schrank um die Ecke geschoben werden muss, damit seine Breite bei gegebener Länge möglichst groß sein kann.
Fertige eine Skizze im Maßstab 1:20 (Flurmaße 2m auf 1,5 m) und schätze die maximale Breite für einen 3 m langen Schrank.
Unter welcher Abänderung der Aufgabenstellung könnte der Schrank auch dann noch "um die Ecke" gebracht werden, wenn er etwas zu breit ist?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Der Schrank muss offenbar so geschoben werden, dass seine rechte Seite die Ecke berührt.
Ein guter Schätzwert ist die Breite des gezeichneten Schranks, also 1 m. Allerdings könnte dies auch bereits etwas zu viel sein.
Falls der Schrank mit 1 Meter zu breit wäre, könnte er vielleicht doch noch "um die Ecke kommen", wenn der Flur hoch genug ist und man den Schrank etwas anheben könnte. Was in der Praxis aber oft durch das Gewicht des Schrankes nicht möglich ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Experimentieren
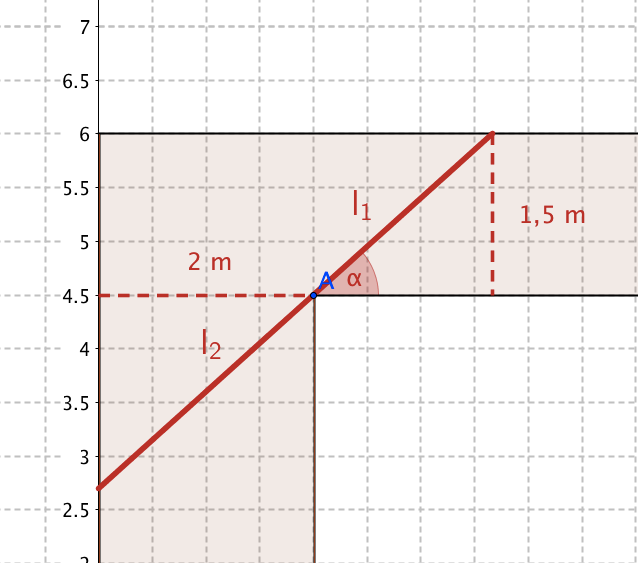
Mit dem gegebenen Geogebra-Applet kannst du die maximale Breite des 3 m langen Schrankes graphisch ermitteln, indem du den Gleiterpunkt B verschiebst.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Der abzulesende Wert für die größtmögliche Breite des Schranks ist rund 0,96 m. Der Schrank aus Teilaufgabe a) mit der Länge von 3 m wäre damit etwas zu breit.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechne für jeden Punkt B die mögliche Schrankbreite b(x).

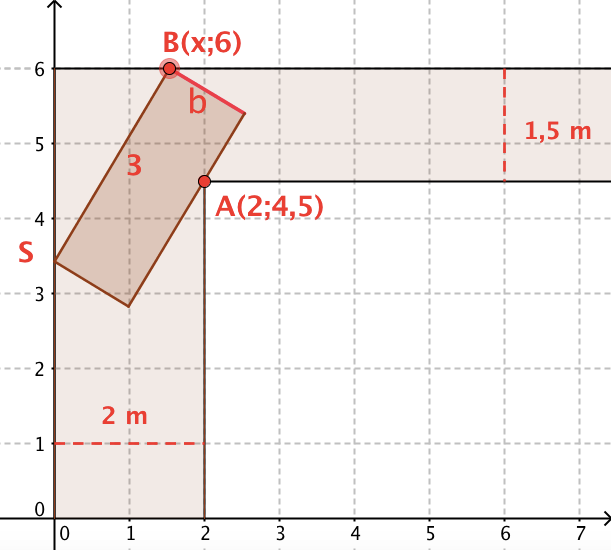
Bestimmung des Minimums der Breitenfunktion b(x)
Die Breitenfunktion b(x) ist definiert von x = 0 bis x = 3. Sie misst für jede Position des Gleitpunktes B den "dicksten" Schrank der gerade noch um die Ecke geschoben werden kann.
Zur Lösung des Schrankproblems braucht man den "dünnsten" aller Schränke, d.h. das Minimum von b(x).
Bestätige für zwei Sonderlagen von B die Richtigkeit des Rechenergebnisses

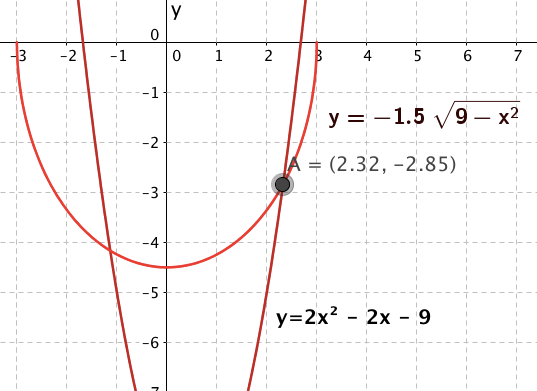
Berechne die Ableitung von b(x) und löse die Gleichung b'(x) = 0 auf graphischem Wege, da sie algebraisch nicht gelöst werden kann.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Produktregel
Die beiden Sonderlagen für den Punkt $B$ sind $x = 0$ (der Schrank steht noch ganz im ersten Flur) und $x = 3$ (der Schrank ist ganz um die Ecke geschoben).
Die Rechnung ergibt: $b(0) = 2$ und $b(3) = 1{,}5$
Bilde die 1. Ableitung von $b(x)$ mit Hilfe der Produktregel und der Kettenregel.
Die Zusammenfassung ergibt:
Setze b'(x) = 0
Multipliziere mit den Nennern und löse die Gleichung graphisch, indem du den Schnittpunkt der Parabel und der Wurzelfunktion (Teil einer Ellipse) ermittelst.
Damit hat man die Lösung unseres Schrankproblems:
Der Punkt $B(2{,}32|6)$ liefert die Schrankbreite $b(2{,}32)$ des Schrankes, der bei der gegebenen Länge von 3 m gerade noch um die Ecke des Flures (2 m auf 1,5 m) geschoben werden kann.
Es gilt:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Und was ist mit einer Vorhangstange?
Bestimme die maximale Länge einer waagrecht getragenen Vorhangstange, die durch den Flur (2 m auf 1,5 m) kommt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel und Kettenregel
l (in Metern) sei die Länge der Stange.
Betrachte die beiden rechtwinkligen Dreiecke, die $\alpha$ enthalten
Setze ein: $\cos\left(\alpha\right)=\sqrt{1-\sin^2\left(\alpha\right)}$
Addiere $l_1$ und $l_2$ und setze
Bilde mit der Quotientenregel und Kettenregell'(x) um die maximale Länge zu ermitteln.
Die Gleichung l'(x) = 0 lässt sich auch hier nicht algebraisch, sondern nur graphisch lösen.
Die x-Koordinate des Schnittpuktes S löst die Gleichung
x = 0,67 (ein Näherungswert!) ist also die Lösung der Gleichung l'(x) = 0 und liefert die längstmögliche Stange.

Eine $4{,}93 \, \text {m}$ lange Stange kann also - waagrecht getragen - in unserem Flur gerade noch um die Ecke getragen werden.
Mit einem anderen Ansatz kann man die Aufgabe sogar allgemein lösen
Das ist eine längere Rechnung, aber zum Ausgleich wirst du mit einem schönen Ergebnis belohnt.
Dazu benötigst du folgendes Grundwissen:
Rechnen mit Potenzen, Kettenregel und Ableiten von Wurzeln.
Weil die Dreiecke mit den Seiten $x,b$ und $u$ einerseits und $y,v$ und $a$ andererseits ähnlich sind, gilt
Die Gesamtlänge $l$ der Stange ist also
Jetzt musst du das Minimum von $l(x)$ bestimmen, indem du die Nullstelle der Ableitung berechnest und das Ergebnis wieder in $l(x)$ einsetzt. Benutze beim Ableiten die Darstellung
Die Ableitung ist nach der Produkt- und Kettenregel
$\displaystyle l'(x)=1+a(x^2-b^2)^{-1/2}+x\cdot a \cdot (-1/2)\cdot (x^2-b^2)^{-3/2}\cdot (2x)$ , also
Um die Nullstelle zu bestimmen, setzt du $l'(x)=0$ und multiplizierst
mit $(x^2-b^2)^{3/2}$ :
Damit erhältst du für den kleinsten Wert von $l$ die Gleichung
und
Dieses Ergebnis kannst du noch umformen:
Das Minimum der Länge $l$ hast du also für $\displaystyle x=\sqrt{a^{2/3}+b^{2/3}}\cdot b^{2/3}$ .
Um die minimale Länge $l$ zu berechnen, setzt du das in die Formel für $l(x)$ ein und benutzt dabei, dass du oben schon ausgerechnet hast, dass
$(x^2-b^2)^{3/2}=ab^2$ ist, also
Jetzt wird
Damit kannst du nun für beliebige Korridorbreiten $a$ und $b$ die maximale Länge einer Vorhangstange bestimmen, die noch waagerecht getragen um die Ecke geht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Peter unternimmt mit seinem Verein eine Floßfahrt. Ob sie aber auch gutgeht?
Mit dem nachfolgenden Geogebra-Applet kannst du experimentell durch Verschieben des Gleiterpunktes G ermitteln, ob der "schwimmende Schrank" (18 m x 4,8 m) um die Flußecke (6 m auf 10 m) kommt.

Böses Ende einer lustigen Floßfahrt: Das Floß bleibt stecken. Es hätte höchstens 4,61 m breit dürfen.
Wie sich die Mannschaft wohl behelfen wird?
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle x_B^2+\left(6-y\left(S\right)\right)^2$	$=$	$\displaystyle 9$	$\displaystyle -x_B^2$
$\displaystyle \left(6-y\left(S\right)\right)^2$	$=$	$\displaystyle 9-x_B^2$	$\displaystyle \sqrt{ }$
$\displaystyle 6-y\left(S\right)$	$=$	$\displaystyle \sqrt{9-x_B^2}$	$\displaystyle -6$
$\displaystyle -y\left(S\right)$	$=$	$\displaystyle -6+\sqrt{9-x_B^2}$	$\displaystyle \cdot\left(-1\right)$
$\displaystyle y\left(S\right)$	$=$	$\displaystyle 6-\sqrt{9-x_B^2}$

$\displaystyle \frac{\sqrt{9-x_B^2}\cdot x-x_B\cdot y+x_B(6-\sqrt{9-x_B^2})}{\sqrt{(9-x_B^2)+x_B^2}}$	$=$	$\displaystyle 0$
$\displaystyle \frac{\sqrt{9-x_B^2}\cdot x-x_B\cdot y+x_B(6-\sqrt{9-x_B^2})}{3}$	$=$	$\displaystyle 0$