Aufgaben zu Kreisen und Kreisteilen

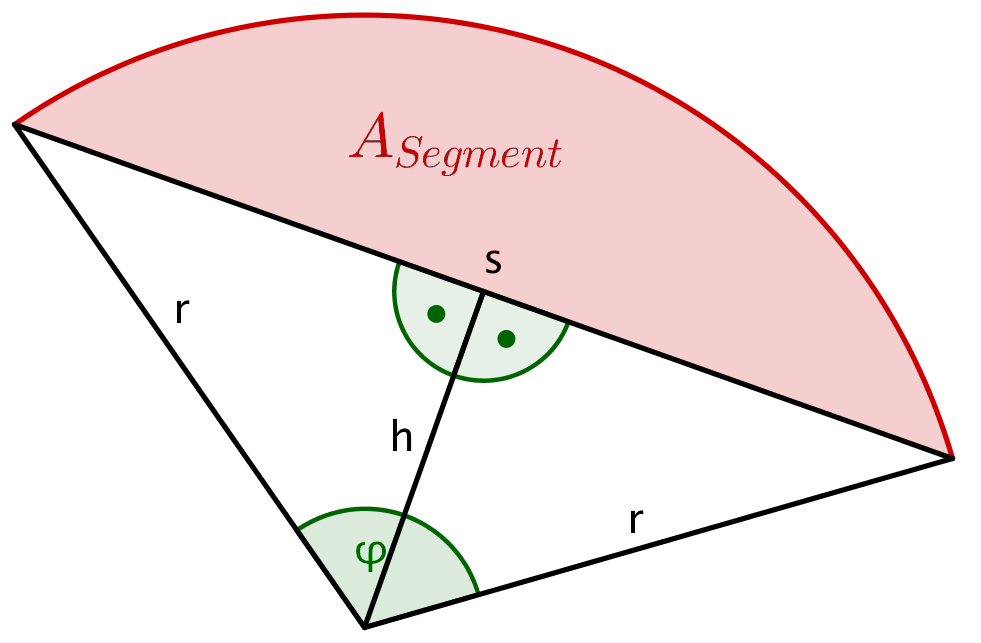
Berechne die Fläche des markierten Kreissegments. Dabei ist der Radius $r = 20 c m$ und $\varphi = 108°$ . Runde deine Lösung auf ganze $\text{cm}^2$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreissektor

r=20cm

$\varphi$ =108°

ges: $A_{Segment}$

Zunächst den Flächeninhalt des Kreissektors berechnen.

$A_{Kreissektor}=\left(20\text{cm}\right)^2\cdot\pi\cdot\frac{108^\circ}{360^\circ}$

$=400cm^2\cdot\pi\cdot\frac3{10}=377\text{cm}^2$

Die Höhe h berechnen, indem man das geteilte, rechtwinklige Dreieck betrachtet und den Cosinus anwendet.

$\displaystyle \cos\left(\frac{\varphi}{2}\right)$	$=$	$\displaystyle \frac{h}{r}$	$\displaystyle \cdot r$
	↓	Die Gleichung nach h umstellen.
$\displaystyle h$	$=$	$\displaystyle \cos\left(54^\circ\right)\cdot20cm=11{,}8\text{cm}$
	↓	Jetzt mit dem Satz von Pythagoras $\frac s2$ berechnen.
$\displaystyle h^2+\left(\frac s2\right)^2$	$=$	$\displaystyle r^2$	$\displaystyle -h^2$
	↓	Nach $\left(\frac s2\right)^2$ umstellen.
$\displaystyle \left(\frac s2\right)^2$	$=$	$\displaystyle r^2-h^2$
	↓	Werte einsetzen.
$\displaystyle \left(\frac s2\right)^2$	$=$	$\displaystyle 400\text{cm}^2-139{,}24\text{cm}^2$
	↓	Subtrahieren und die Wurzel ziehen.
$\displaystyle \frac s2$	$=$	$\displaystyle 16{,}1\text{cm}$
	↓	s berechnen, indem man $\frac s2$ mit 2 multipliziert.
$\displaystyle s$	$=$	$\displaystyle 16{,}1\text{cm}\cdot2$
$\displaystyle s$	$=$	$\displaystyle 32{,}2\text{cm}$

Den Flächeninhalt des Dreiecks berechnen, dessen Seiten r, r und s sind.

$\displaystyle A_{Dreieck}$	$=$	$\displaystyle \frac12\cdot s\cdot h$
	↓	Werte einsetzen
	$=$	$\displaystyle \frac12\cdot32{,}2\text{cm}\cdot11{,}8\text{cm}$
	$=$	$\displaystyle 190\text{cm}^2$

Den Flächeninhalt des Dreiecks vom Kreissektor subtrahieren.

$A_{Segment}=A_{Kreissektor}-A_{Dreieck}$

$=377\text{cm}^2-190\text{cm}^2=187\text{cm}^2$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl → Was bedeutet das?