Gemischte Aufgaben zur Volumenberechung

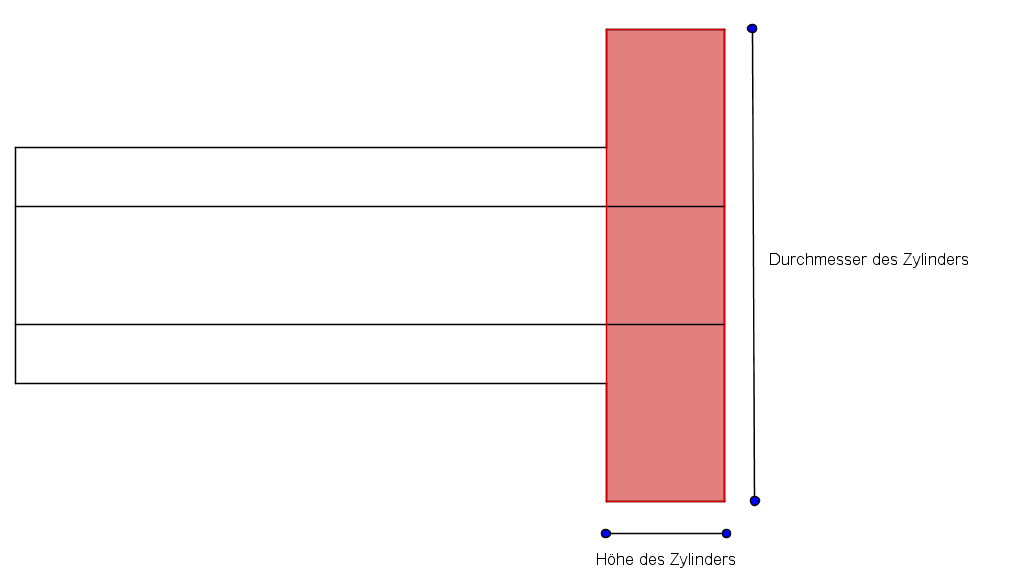
Zu berechnen ist die Masse der Bronze-Lagerbuchse (CuSn8). Auf welchen Bruchteil in % verringert sie sich, wenn man sie aus Kunststoff herstellt?

$ρ_{B r o n z e} = 8,6 \frac{k g}{d m^{3}}; ρ_{K u n s t s t o f f} = 2,2 \frac{k g}{d m^{3}}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen

Um das Gewicht des Objekts zu erhalten, berechnest du zunächst das Volumen und dann ergibt der Term "Volumen $\cdot$ Dichte" das Gewicht. Da die Dichte in kg/dm³ angegeben ist, verwendest du am besten schon in allen Zwischenschritten die Längeneinheit dm statt m.

Bei der Buchse handelt es sich nun um einen Rotationskörper, den du aus Zylindern zusammensetzen kannst.

Die Volumenformel für Zylinder lautet $V = π r^{2} h$ .

Du beginnst am besten von außen, d.h. ganz rechts an der breitesten Stelle.

Die Höhe des Zylinders (hier von waagrecht eingezeichnet) berechnest du als $65 m m - 57 m m = 8 m m = 0,08 d m$ .

Der Durchmesser ist die höchste Stelle der Buchse und damit $60 m m$ . Der Radius $r$ ist die Hälfte davon und also $30 m m$ bzw $0,3 d m$ .

Damit ergibt sich mit der Volumenformel: $V = π \cdot (0,3 d m)^{2} \cdot 0,08 d m = 0,0226 d m^{3}$

Als nächstes berechnest du das Volumen der Röhre. Als Höhe dieses Rotationszylinders hast du die vollen $65 m m$ also $6,5 d m$ gegeben und der Durchmesser (hier wieder senkrecht) ist $34 m m - 24 m m = 10 m m = 0,1 d m$ und damit der Radius $r = 0,05 d m$ .

Es ergibt sich $V = π \cdot (0,05 d m)^{2} \cdot 6,5 d m = 0,0511 d m^{3}$ .

Als bisherige Summe ergibt sich also $0,0737 d m^{3}$ .

Da du nun einen Teil der Fläche doppelt gezählt hast, ziehst du diesen wieder ab. Dazu musst du natürlich bestimmen, welches Volumen dieser Teil hat. Berechnet wird dieses ebenso wie zuvor schon zwei mal:

Höhe des Rotationszylinders ist $65 m m - 75 m m = 8 m m = 0,08 d m$

Radius des Zylinders ist $r = \frac{1}{2}$ Durchmesser $= \frac{1}{2} \cdot 34 m m = 17 m m = 0,17 d m$

Damit ergibt sich das Volumen als $V = π \cdot (0,08 d m^{2} \cdot 0,17 d m = 0,0034 d m^{3}$

Ziehst du dies von der bisherigen Summe ab, erhältst du als neues Zwischenergebnis $0,0703 d m^{3}$ .

Jetzt musst du nur noch den Teil des Volumens der Röhre abziehen, den du noch nicht abgezogen hast.

Die Höhe dieses Zylinders (wieder waagrecht) ist $57 m m = 0,57 d m$

Der Durchmesser ist $24 m m = 0,24 d m$ und damit der Radius $0,12 d m$ .

Das Volumen ist also $V = π \cdot π \cdot (0,12 d m)^{2} \cdot \cdot 0,57 d m = 0,0258 d m^{3}$

$V = π \cdot (0,12 d m)^{2} \cdot 0,57 d m = 0,0258 d m^{3}$ Zieht man das von der bisherigen Zwischensumme ab, erhält man

$V = 0,0703 d m^{3} - 0,0258 d m^{3} = 0,0445 d m^{3}$

Damit erhält man das Ergebnis: Das Gewicht in Bronze ist $G = 8,6 \cdot \cdot 0,0445 k g = 0,3827 k g$

und das Gewicht in Kunststoff ist $2,2 \cdot 0,0445 k g = 0,0979 k g$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?