Aufgaben zu Volumen, Masse und Dichte
Lerne mit diesen gemischten Übungsaufgaben, Volumen, Masse und Dichte von Körpern zu berechnen.
- 1
In einem Ölbehälter (Quader) mit den Abmessungen a=500 mm, b=300 mm, c=250 mm ist m=25 kg Öl vorhanden.
Dichte von Öl:
Welche Höhe h in mm hat der Ölspiegel?
mm - 2
Ein quaderförmiges Werkstück it den Maßen a=10 mm, b=60 mm, c=150 mm hat eine Masse von m=657 g.
Welche Dichte hat das Material?
kg/dm³ - 3
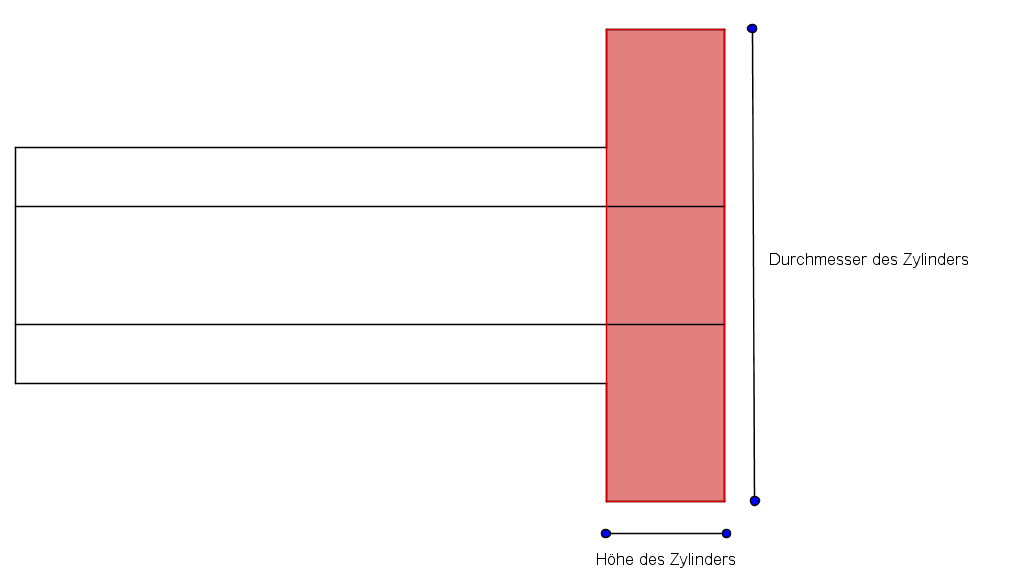
Eine Buchse (Rohrstück) aus CuSn 10 mit der Dichte
hat die Durchmesser , und die Länge .
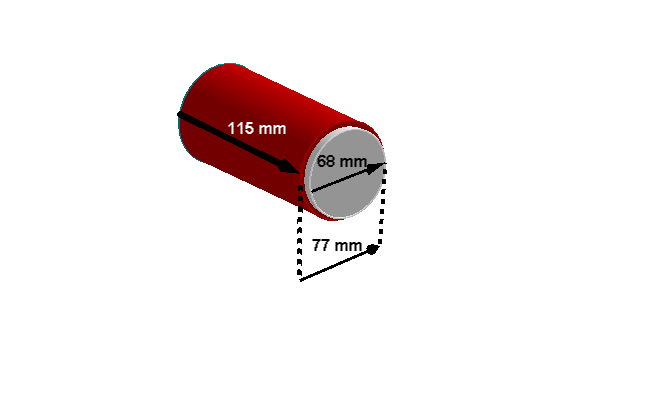
Berechnen Sie die Masse in kg und runde auf 3 Dezimalstellen.
kg - 4
Ein rotationssymmetrisches Werkstück soll aus Gusseisen der Dichte hergestellt werden.
Das Bild zeigt das Werkstück im Querschnitt. Berechne die Masse des Werkstücks.
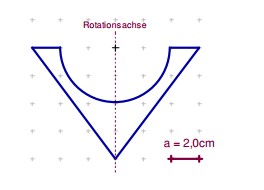
- 5
Berechne Volumen und Masse des Stahlteils. Alle Längen sind in Millimeter angegeben.
Dichte:

- 6
Berechne Volumen und Masse des Kupferteils. Das Material ist 12 mm dick.
Dichte:

- 7
Ein Stahlrohr ist 10 m lang (), hat einen Außendurchmesser von und einen Innendurchmesser von .
Berechnen Sie das Volumen, die Masse und die Wandstärke des Rohres.

- 8
Berechne Volumen und Masse des Aluminiumteils. Die Seitenlängen sind in Millimetern angegeben.
Dichte:

Die Längen in der Zeichnung sind in Millimeter angegeben.
- 9
Eine Drahtrolle aus d=0,5mm dickem Stahldaht
hat eine Masse von m=3,6kg.
Wie viel Meter sind auf der Rolle?
- 10
Berechnen Sie die Masse von 20 Lagerzapfen aus S235J2 (St 37 -3) für Garagentore.
Stahl hat eine Dichte von

- 11
Zu berechnen ist die Masse der Bronze-Lagerbuchse (CuSn8). Auf welchen Bruchteil in % verringert sie sich, wenn man sie aus Kunststoff herstellt?

- 12
Berechne Volumen und Masse des Gussteils.
Dichte:

Die Längen in der Zeichnung sind in angegeben.
- 13
Herr Krösus hat für den Weihnachtsbaum einen Stern aus Gold gekauft.
Der Stern ist dick. Gold hat eine Dichte von .
Ein Gramm Gold kostet etwa .
Die Maße des Weihnachtssterns kannst du der Zeichnung entnehmen.
Wie teuer war der Weihnachtsstern?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?