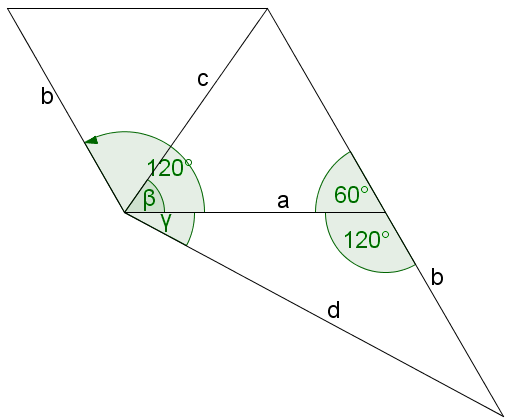
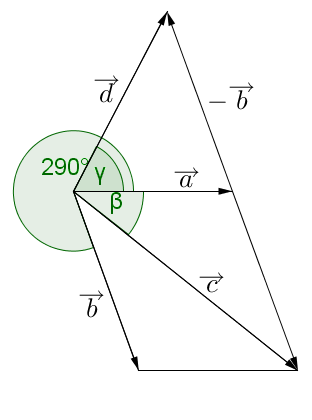
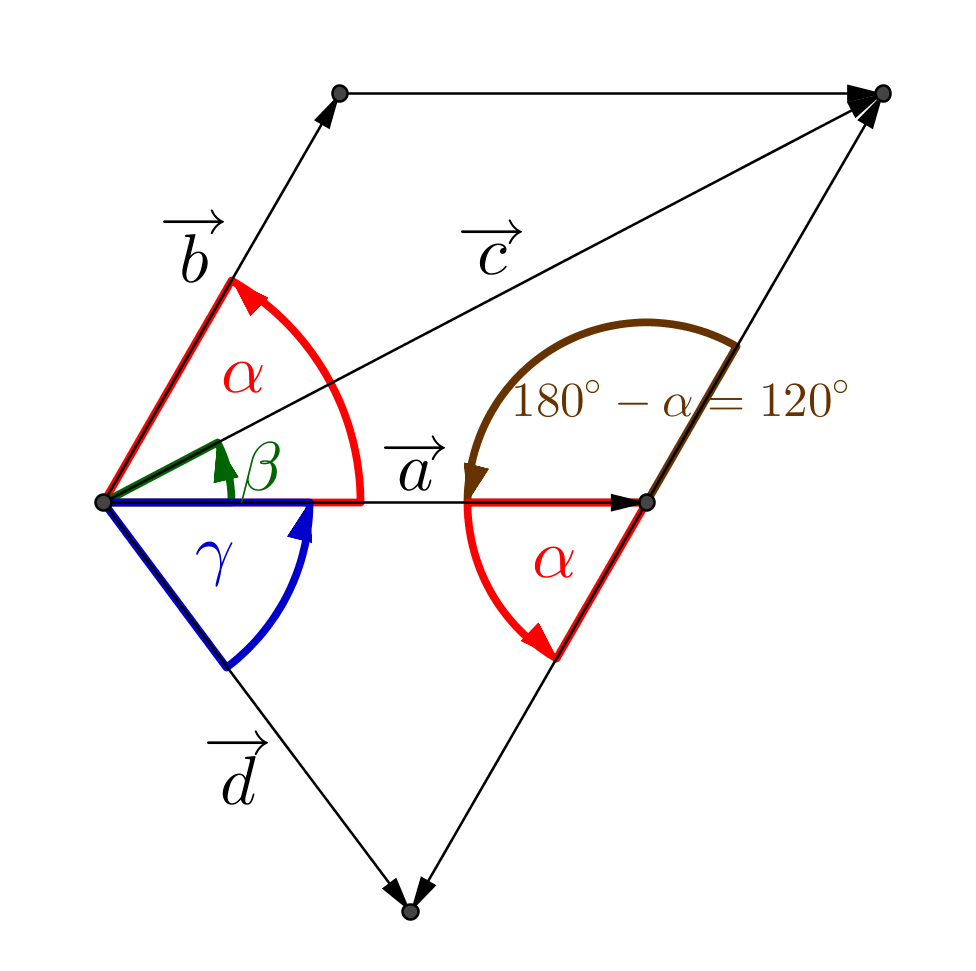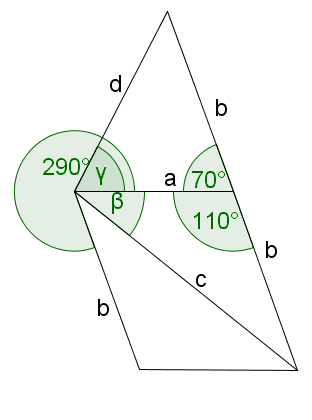Aufgaben zum dreidimensionalen Koordinatensystem

Zwei Vektoren $\vec{a}$ und $\vec{b}$ schließen den Winkel $α$ miteinander ein.

Die Vektoren $\vec{c}$ und $\vec{d}$ setzen sich aus $\vec{a}$ und $\vec{b}$ wie folgt zusammen:

$\vec{c} = \vec{a} + \vec{b}$ und $\vec{d} = \vec{a} - \vec{b}$

Die Vektoren $\vec{a}$ und $\vec{c}$ schließen den Winkel $β$ ein. Die Vektoren $\vec{d}$ und $\vec{a}$ schließen den Winkel $γ$ ein.

Betrachte die folgenden Angaben zu $| \vec{a} |$ , $| \vec{b} |$ unc $α$ .

1) Zeichne die Vektoren. Die Richtung der Vektoren ist hierbei egal. Nur deren Länge und eingeschlossener Winkel $α$ .

2) Bestimme zeichnerisch die Länge von $\vec{c}$ und $\vec{d}$ .

3) Lies aus deiner Zeichnung die Winkel $β$ und $γ$ ab.

4) Berechne die Länge von $\vec{c}$ und $\vec{d}$ .

5) Berechne die Winkel $β$ und $γ$ .

Alle Längeneinheiten sind in $cm$ angegeben.

123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
$| \vec{a} | = a = 4,6$ ; $| \vec{b} | = b = 4,0$ ; $α = ∢ (\vec{a}, \vec{b}) = 60^{\circ}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
1) Vektoren zeichnen
Zeichne zunächst Vektor $\vec{a}$ ein. Die Richtung ist egal. Entscheidend ist die Länge von 4,6.
Zeichne dann den Vektor $\vec{b}$ im Winkel von $α = 60^{\circ}$ an den Fuß von Vektor $\vec{a}$ ein. Der Winkel wird gegen den Uhrzeigersinn gemessen.
Nun fehlen noch die Vektoren $\vec{c}$ und $\vec{d}$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
Zeichnet man Vektor $\vec{b}$ im selben Winkel und mit derselben Länge an die Spitze von Vektor $\vec{a}$ , so erhalten wir ein Parallelogramm, welches in der Diagonale den Vektor $\vec{a} + \vec{b} = \vec{c}$ besitzt.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit derselben Länge - aber in entgegengesetzter Richtung - an die Spitze von $\vec{a}$ ein, so erhält man vom Fuß von $\vec{a}$ bis zur Spitze von $- \vec{b}$ den Vektor $\vec{a} - \vec{b} = \vec{d}$ .
2) $| \vec{c} |$ und $| \vec{d} |$ zeichnerisch bestimmen
Nun kannst du die Länge von $\vec{c}$ und $\vec{d}$ aus der Zeichnung ablesen:
$| \vec{c} | \approx 7,4$ und $| \vec{d} | \approx 4,3$
3) $β$ und $γ$ aus der Zeichnung ablesen
Miss die Winkel $β$ und $γ$ ab:
$β \approx {27,7}^{\circ}$
$γ \approx {53,1}^{\circ}$
4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch betimmen
Verwende den Kosinussatz:
$c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos (120^{\circ}) \Rightarrow c = | \vec{c} | \approx 7,454$
$d^{2} = a^{2} + b^{2} - 2 a b \cdot \cos (60^{\circ}) \Rightarrow d = | \vec{d} | \approx 4,331$
5) $β$ und $γ$ rechnerisch bestimmen
Für die Winkel $β$ und $γ$ kann man sich wieder den Kosinussatz zu nutze machen:
$\begin{array}{l} b^{2} = a^{2} + c^{2} - 2 ac \cdot \cos (β) \\ \Rightarrow \cos (β) = \frac{a^{2} + c^{2} - b^{2}}{2 a c} \\ \Rightarrow β \approx {27,693}^{\circ} \end{array}$
$\begin{array}{l} b^{2} = a^{2} + d^{2} - 2 a d \cdot \cos (γ) \\ \Rightarrow \cos (γ) = \frac{a^{2} + d^{2} - b^{2}}{2 a d} \\ \Rightarrow γ \approx {53,11}^{\circ} \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
$| \vec{a} | = a = 4,2$ ; $| \vec{b} | = b = 3,8$ ; $α = ∢ (\vec{a}, \vec{b}) = 120^{\circ}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
1) Vektoren zeichnen
Zeichne zunächst Vektor $\vec{a}$ ein. Die Richtung ist egal. Entscheident ist die Länge von 4,2.
Dann zeichnet man den Vektor $\vec{b}$ im Winkel von $α = 120^{\circ}$ gegen den Uhrzeigersinn an den Fuß von Vektor $\vec{a}$ ein.
Nun fehlen noch die Vektoren $\vec{c}$ und $\vec{d}$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit der selben Länge an die Spitze von Vektor $\vec{a}$ so erhalten wir ein Parralelogramm, dass in der Diagonale den Vektor $\vec{a} + \vec{b} = \vec{c}$ besitzt.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit der selben Länge, aber in der entgegengesetzten Richtung ein, so erhält man vom Fuß von $\vec{a}$ bis zur Spitze von - $\vec{b}$ den Vektor $\vec{a} - \vec{b} = \vec{d}$ .
2) $| \vec{c} |$ und zeichnerisch bestimmen
Messe die Länge der Vektoren $\vec{c} und \vec{d}$ ab.
$| \vec{c} | \approx 4,0$
$| \vec{d} | \approx 6,9$
3) $β$ und $γ$ aus der Zeichnung ablesen
Miss die Winkel $β$ und $γ$ ab:
$β \approx {54,9}^{\circ}$
$γ \approx {28,3}^{\circ}$
4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch bestimmen
Zunächst müssen wir die Winkel an der Spitze von a ermitteln. Durch den Z-Winkel sind unten 120° vorzufinden und oben 60°, da diese beiden Winkel insgesamt 180° ergeben müssen.
Gesucht ist nun erst mal die Seite c. Um diese zu berechnen benutzen wir den Kosinussatz über die Seiten a und b und dem Winkel von 60°.
Um d zu berechnen gehen wir genauso vor. Wir rechnen mit dem Kosinussatz über die Seiten a und b und dem Winkel von 120°.
$c^{2} = a^{2} + b^{2} - 2 ab \cdot \cos (60^{\circ}) \Rightarrow c = | \vec{c} | \approx 4,015$
$d^{2} = a^{2} + b^{2} - 2 ab \cdot \cos (120^{\circ}) \Rightarrow d = | \vec{d} | \approx 6,931$
5) $β$ und $γ$ rechnerisch bestimmen
Für die Winkel $β und γ$ kann man sich wieder den Kosinussatz zu nutze machen.
Hierfür rechnen wir erst b über c, a und dem Winkel $β$ und formen dann nach $\cos (β)$ um.
Das selbe machen wir mit $\cos (γ)$ .
$\begin{array}{l} b^{2} = a^{2} + c^{2} - 2 ac \cdot \cos (β) \\ \Rightarrow \cos (β) = \frac{a^{2} + c^{2} - b^{2}}{2 ac} \\ \Rightarrow β \approx {55,05}^{\circ} \end{array}$

$\begin{array}{l} b^{2} = a^{2} + d^{2} - 2 ad \cdot \cos (γ) \\ \Rightarrow \cos (γ) = \frac{a^{2} + d^{2} - b^{2}}{2 ad} \\ \Rightarrow γ \approx {28,346}^{\circ} \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
$| \vec{a} | = a = 4,7$ ; $| \vec{b} | = b = 3,2$ ; $α = ∢ (\vec{a}, \vec{b}) = 250^{\circ}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
1) Vektoren zeichnen
Zeichne zunächst Vektor $\vec{a}$ ein. Richtung ist egal. Entscheident ist die Länge von 4,7.
Dann zeichnet man den Vektor $\vec{b}$ im Winkel von $α = 250^{\circ}$ gegen den Uhrzeigersinn an den Fuß von Vektor $\vec{a}$ ein.
Nun fehlen noch die Vektoren $\vec{c}$ und $\vec{d}$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit der selben Länge an die Spitze von Vektor $\vec{a}$ so erhalten wir ein Parralelogramm, dass in der Diagonale den Vektor $\vec{a} + \vec{b} = \vec{c}$ besitzt.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit der selben Länge, aber in der entgegengesetzten Richtung ein, so erhält man vom Fuß von $\vec{a}$ bis zur Spitze von - $\vec{b}$ den Vektor $\vec{a} - \vec{b} = \vec{d}$ .
2) $\vec{c}$ und $\vec{d}$ zeichnerisch bestimmen
Messe die Länge der Vektoren $\vec{c} und \vec{d}$ ab.
$| \vec{c} | \approx 4,7$
$| \vec{d} | \approx 6,5$
3) $β$ und $γ$ aus der Zeichnung ablesen
Miss die Winkel $β$ und $γ$ ab:
$β \approx {39,8}^{\circ}$
$γ \approx {27,4}^{\circ}$
4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch bestimmen
Zunächst müssen wir die Winkel an der Spitze von a ermitteln.
Dafür brauchen wir den Winkel den b im Uhrzeigesinn von a entfernt ist. Dieser beträgt $α - 180^{\circ} = 70^{\circ}$ .
Durch den Z-Winkel sind nun an der Spitze von a unten 70° vorzufinden und oben 110°, da diese beiden Winkel insgesamt 180° ergeben müssen.
Gesucht ist nun erst mal die Seite c. Um diese zu berechnen benutzen wir den Kosinussatz über die Seiten a und b und dem Winkel von 70°.
Um d zu berechnen gehen wir genauso vor. Wir rechnen mit dem Kosinussatz über die Seiten a und b und dem Winkel von 110°.
$c^{2} = a^{2} + b^{2} - 2 ab \cdot \cos (70^{\circ}) \Rightarrow c = | \vec{c} | \approx 4,695$
$d^{2} = a^{2} + b^{2} - 2 ab \cdot \cos (110^{\circ}) \Rightarrow d = | \vec{d} | \approx 6,528$
5) $β$ und $γ$ rechnerisch bestimmen
Für die Winkel $β und γ$ kann man sich wieder den Kosinussatz zu nutze machen.
Hierfür rechnen wir erst b über c, a und dem Winkel $β$ und formen dann nach $\cos (β)$ um.
Das selbe machen wir mit $\cos (γ)$ .
$\begin{array}{l} b^{2} = a^{2} + c^{2} - 2 ac \cdot \cos (β) \\ \Rightarrow \cos (β) = \frac{a^{2} + c^{2} - b^{2}}{2 ac} \\ \Rightarrow β \approx {39,828}^{\circ} \end{array}$

$\begin{array}{l} b^{2} = a^{2} + d^{2} - 2 ad \cdot \cos (γ) \\ \Rightarrow \cos (γ) = \frac{a^{2} + d^{2} - b^{2}}{2 ad} \\ \Rightarrow γ \approx {27,427}^{\circ} \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
$| \vec{a} | = a = 3,5$ ; $| \vec{b} | = b = 4,2$ ; $α = ∢ (\vec{a}, \vec{b}) = 290^{\circ}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
1) Vektoren zeichnen
Zeichne zunächst Vektor $\vec{a}$ ein. Richtung ist egal. Entscheident ist die Länge von 3,5.
Dann zeichnet man den Vektor $\vec{b}$ im Winkel von $α = 290^{\circ}$ gegen den Uhrzeigersinn an den Fuß von Vektor $\vec{a}$ ein.
Nun fehlen noch die Vektoren $\vec{c}$ und $\vec{d}$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit der selben Länge an die Spitze von Vektor $\vec{a}$ so erhalten wir ein Parralelogramm, dass in der Diagonale den Vektor $\vec{a} + \vec{b} = \vec{c}$ besitzt.
Zeichnet man Vektor $\vec{b}$ nun im selben Winkel und mit der selben Länge, aber in der entgegengesetzten Richtung ein, so erhält man vom Fuß von $\vec{a}$ bis zur Spitze von - $\vec{b}$ den Vektor $\vec{a} - \vec{b} = \vec{d}$ .
2) $| \vec{c} |$ und $| \vec{d} |$ zeichnerisch bestimmen
Messe die Länge der Vektoren $\vec{c} und \vec{d}$ ab.
$| \vec{c} | \approx 6,3$
$| \vec{d} | \approx 4,5$
3) $β$ und $γ$ aus der Zeichnung ablesen
Miss die Winkel $β$ und $γ$ ab:
$β \approx {38,6}^{\circ}$
$γ \approx {62,3}^{\circ}$
4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch bestimmen
$\vec{c}$ und $\vec{d}$ rechnerisch bestimmen mit Kosinussatz
Zunächst müssen wir die Winkel an der Spitze von a ermitteln.
Dafür brauchen wir den Winkel den b im Uhrzeigesinn von a entfernt ist. Dieser beträgt $α - 180^{\circ} = 110^{\circ}$ .
Durch den Z-Winkel sind nun an der Spitze von a unten 110° vorzufinden und oben 70°, da diese beiden Winkel insgesamt 180° ergeben müssen.
Gesucht ist nun erst mal die Seite c. Um diese zu berechnen benutzen wir den Kosinussatz über die Seiten a und b und dem Winkel von 110°.
Um d zu berechnen gehen wir genauso vor. Wir rechnen mit dem Kosinussatz über die Seiten a und b und dem Winkel von 70°.
$c^{2} = a^{2} + b^{2} - 2 ab \cdot \cos (110^{\circ}) \Rightarrow c = | \vec{c} | \approx 6,32$
$d^{2} = a^{2} + b^{2} - 2 ab \cdot \cos (70^{\circ}) \Rightarrow d = | \vec{d} | \approx 4,454$
5) $β$ und $γ$ rechnerisch bestimmen
Für die Winkel $β und γ$ kann man sich wieder den Kosinussatz zu nutze machen.
Hierfür rechnen wir erst b über c, a und dem Winkel $β$ und formen dann nach $\cos (β)$ um.
Das selbe machen wir mit $\cos (γ)$ .
$\begin{array}{l} b^{2} = a^{2} + c^{2} - 2 ac \cdot \cos (β) \\ \Rightarrow \cos (β) = \frac{a^{2} + c^{2} - b^{2}}{2 ac} \\ \Rightarrow β \approx {38,642}^{\circ} \end{array}$

$\begin{array}{l} b^{2} = a^{2} + d^{2} - 2 ad \cdot \cos (γ) \\ \Rightarrow \cos (γ) = \frac{a^{2} + d^{2} - b^{2}}{2 ad} \\ \Rightarrow γ \approx {62,397}^{\circ} \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

1) Vektoren zeichnen

2) |c→| und |d→| zeichnerisch bestimmen

3) β und γ aus der Zeichnung ablesen

4) |c→| und |d→| rechnerisch betimmen

5) β und γ rechnerisch bestimmen

Hast du eine Frage oder Feedback?

1) Vektoren zeichnen

2) |c→| und zeichnerisch bestimmen

3) β und γ aus der Zeichnung ablesen

4) |c→| und |d→| rechnerisch bestimmen

5) β und γ rechnerisch bestimmen

Hast du eine Frage oder Feedback?

1) Vektoren zeichnen

2) c→ und d→ zeichnerisch bestimmen

3) β und γ aus der Zeichnung ablesen

4) |c→| und |d→| rechnerisch bestimmen

5) β und γ rechnerisch bestimmen

Hast du eine Frage oder Feedback?

1) Vektoren zeichnen

2) |c→| und |d→| zeichnerisch bestimmen

3) β und γ aus der Zeichnung ablesen

4) |c→| und |d→| rechnerisch bestimmen

5) β und γ rechnerisch bestimmen

Hast du eine Frage oder Feedback?

2) $| \vec{c} |$ und $| \vec{d} |$ zeichnerisch bestimmen

3) $β$ und $γ$ aus der Zeichnung ablesen

4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch betimmen

5) $β$ und $γ$ rechnerisch bestimmen

2) $| \vec{c} |$ und zeichnerisch bestimmen

3) $β$ und $γ$ aus der Zeichnung ablesen

4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch bestimmen

5) $β$ und $γ$ rechnerisch bestimmen

2) $\vec{c}$ und $\vec{d}$ zeichnerisch bestimmen

3) $β$ und $γ$ aus der Zeichnung ablesen

4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch bestimmen

5) $β$ und $γ$ rechnerisch bestimmen

2) $| \vec{c} |$ und $| \vec{d} |$ zeichnerisch bestimmen

3) $β$ und $γ$ aus der Zeichnung ablesen

4) $| \vec{c} |$ und $| \vec{d} |$ rechnerisch bestimmen

5) $β$ und $γ$ rechnerisch bestimmen