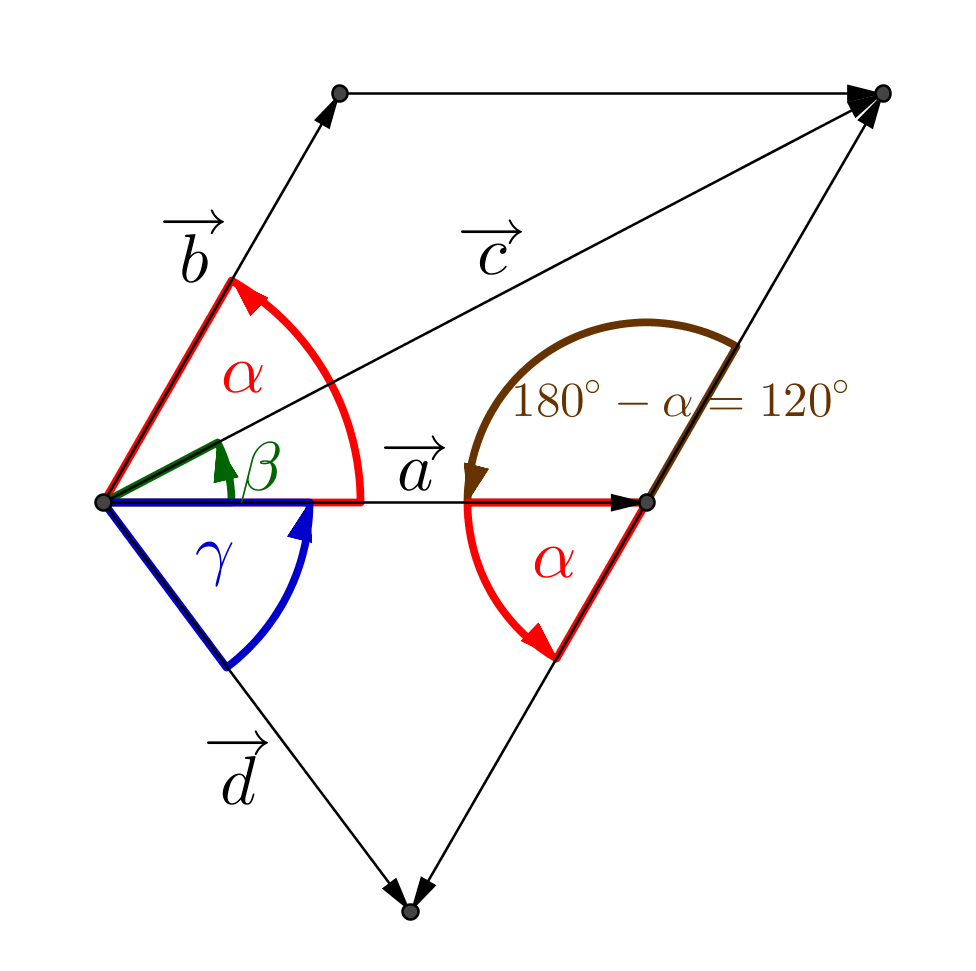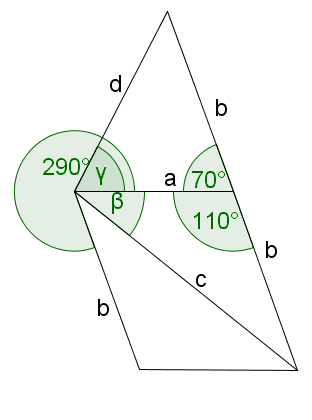Aufgaben zum dreidimensionalen Koordinatensystem

Hier findest du gemischte Aufgaben zu Vektoren im dreidimensionalen Koordinatensystem. Lerne, Vektoren zu konstruieren und wichtige Größen zu berechnen.

1
Ziehe die Achsenbeschriftung zu den richtigen Achsen und die Punktkoordinaten zur korrekten roten Markierung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreidimensionales Koordinatensystem
Gehe von den gegebenen Koordinaten aus und schaue, zu welchem Kreuz sie passen. Jeder Punkt ist eindeutig.
2
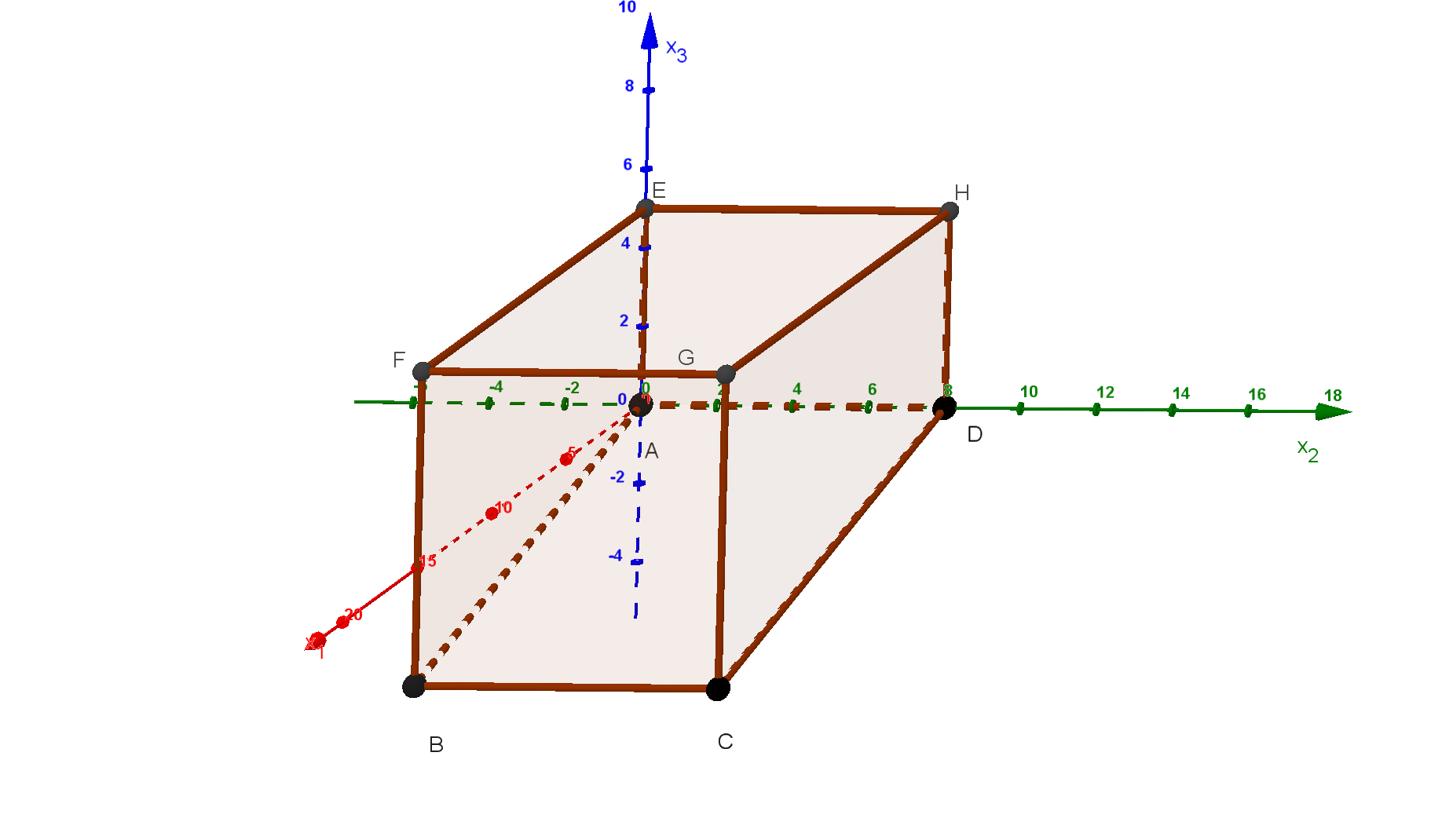
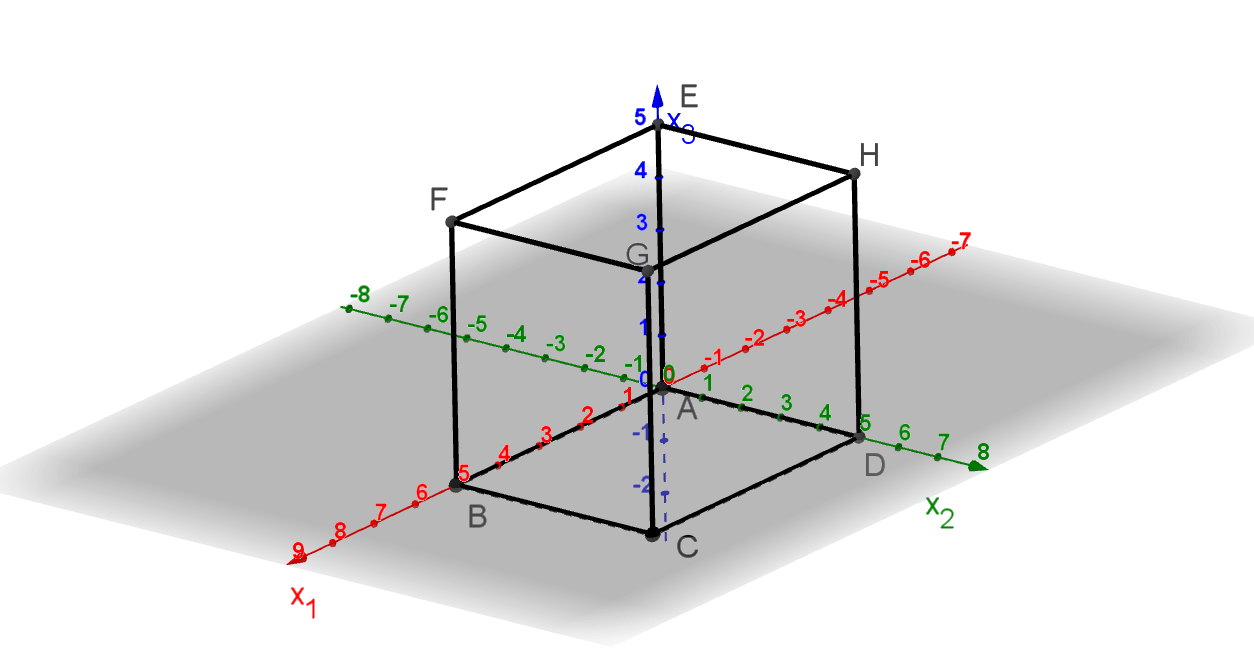
Der unten abgebildete Würfel ABCDEFGH hat unter anderem die Eckpunkte A(0|0|0) und
B(5|0|0).

Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreidimensionales Koordinatensystem
Überlege dir, welche Koordinaten die Punkte C, E und H mit den Punkten A bzw B gemeinsam haben. Bedenke, dass im Würfel alle Seiten gleich lang sind.
3
Ein Haus soll in einen Hang gebaut werden. Dafür muss aus diesem Erde abgetragen werden, um das 15m breite und 8m lange Haus zu platzieren.
Die vier sichtbaren unteren Eckpunkte des Hauses bilden das Viereck ABCD, das schräg im Raum liegt. Dabei gilt $A(0|0|0)$ und $B(15|0|-3)$ .
Alles unterhalb des Punktes A entspricht im fertigen Haus dem Kellergeschoss, wobei alles unterhalb des Vierecks ABCD ausgehoben wurde. Darüber befinden sich zwei Stockwerke mit einer Deckenhöhe von jeweils 2,50m. Das Haus hat ein Flachdach.
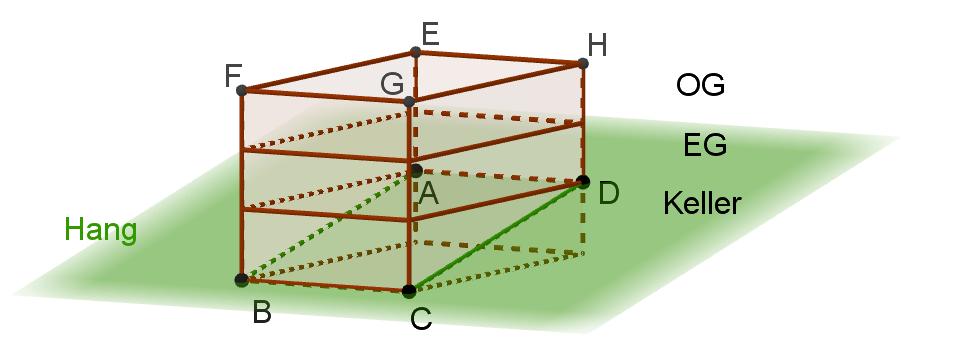
Haus im Hang
1. Gib die Koordinaten aller übrigen Punkte C, D, E, F, G und H an und zeichne das Haus in ein geeignetes Koordinatensystem.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreidimensionales Koordinatensystem
  Koordinatensystem anlegen
  Ein sinnvoller Maßstab ist: $1m \hat{=}1cm$
  Überlege dir vorher den Platzbedarf:
  Das Haus ist 15 Meter lang, diese Größe kannst du auf die $x_1$ -Achse setzen.
  Es ist 8 Meter breit, was der nötigen Länge in $x_2$ Richtung entspricht
  Insgesamt hat das Haus einen 3 Meter tiefen Keller und die zwei Stockwerke sind zusammen 5m hoch. Die $x_3$ -Achse sollte also mindestens von -3 bis 5 reichen.
  Punkte einzeichnen
  Hast du A und B platziert, kannst du entsprechend der Skizze den Punkt C 8 cm rechts von B platzieren und den Punkt D 8 cm rechts von A.
  Die Punkte E und H liegen senkrecht über A und D auf einer Höhe von 5 cm.
  F und G liegen senkrecht über B und C, aber auf der gleichen Höhe wie E und F.
  Damit ergeben sich die Koordinaten:
  $A(0|0|0), B(15|0|-3), C(15|8|-3), D(0|8|0), E(0|0|5), F(15|0|5), G(15|8|5)$ und $H(0|8|5)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme, wie viel Liter Erde ausgehoben werden müssen, um das Haus zu bauen.
  Liter
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quader
  Volumen berechnen
  Das Kellergeschoss ist ein Quader mit den Seitenlängen 8m, 15m und 3m, also
  $V_{\text{Keller}}=8m\cdot 3m\cdot15m=360m^3$
  Allerdings ist nur die Hälfe dieses Volumens im Hang und muss ausgehoben werden:
  $V_{\text{Aushub}}=360m^3:2=180m^3$
  Umrechnung in Liter
  Damit du angeben kannst, wie viel Liter Erde das sind, musst du in $dm^3$ umrechnen.
  $V_{\text{Aushub}}=180m^3=180\; 000dm^3=180\;000l$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Du kannst zum Beispiel zuerst das Volumen des gesamten Kellers bestimmen.
  Überlege anschließend: Die Strecke $\overline{CD}$ ist die Diagonale des Recktecks, das die Seitenfläche des Kellers beschreibt. Welche Auswirkungen hat das auf das Volumen?
4
Zwei Vektoren $\overrightarrow{\mathrm a}$ und $\overrightarrow{\mathrm b}$ schließen den Winkel $\mathrm\alpha$ miteinander ein.
Die Vektoren $\vec c$ und $\vec d$ setzen sich aus $\vec a$ und $\vec b$ wie folgt zusammen:
$\overrightarrow c=\overrightarrow a+\overrightarrow b$ und $\overrightarrow d=\overrightarrow a-\overrightarrow b$
Die Vektoren $\vec a$ und $\vec c$ schließen den Winkel $\beta$ ein. Die Vektoren $\vec d$ und $\vec a$ schließen den Winkel $\gamma$ ein.
Betrachte die folgenden Angaben zu $\left|\vec{a}\right|$ , $\left|\vec{b}\right|$ unc $\alpha$ .
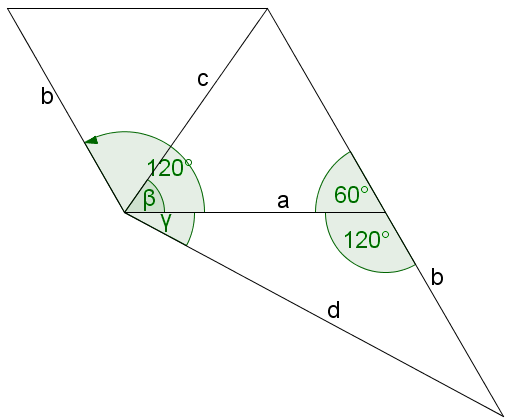
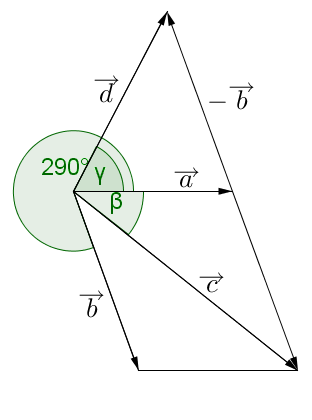
1) Zeichne die Vektoren. Die Richtung der Vektoren ist hierbei egal. Nur deren Länge und eingeschlossener Winkel $\alpha$ .
2) Bestimme zeichnerisch die Länge von $\vec c$ und $\vec d$ .
3) Lies aus deiner Zeichnung die Winkel $\beta$ und $\gamma$ ab.
4) Berechne die Länge von $\vec c$ und $\vec d$ .
5) Berechne die Winkel $\beta$ und $\gamma$ .
Alle Längeneinheiten sind in $\text{cm}$ angegeben.
1. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $\left|\overrightarrow{\mathrm a}\right|=\mathrm a=4{,}6$ ; $\left|\overrightarrow{\mathrm b}\right|=\mathrm b=4{,}0$ ; $\mathrm\alpha=\sphericalangle\left(\overrightarrow{\mathrm a},\overrightarrow{\mathrm b}\right)=60^\circ$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
  1) Vektoren zeichnen
  Zeichne zunächst Vektor $\overrightarrow{\mathrm a}$ ein. Die Richtung ist egal. Entscheidend ist die Länge von 4,6.
  Zeichne dann den Vektor $\overrightarrow{\mathrm b}$ im Winkel von $\mathrm\alpha=60^\circ$ an den Fuß von Vektor $\overrightarrow{\mathrm a}$ ein. Der Winkel wird gegen den Uhrzeigersinn gemessen.
  Nun fehlen noch die Vektoren $\vec c$ und $\vec d$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ im selben Winkel und mit derselben Länge an die Spitze von Vektor $\overrightarrow{\mathrm a}$ , so erhalten wir ein Parallelogramm, welches in der Diagonale den Vektor $\overrightarrow{\mathrm a}+\overrightarrow{\mathrm b}=\overrightarrow{\mathrm c}$ besitzt.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit derselben Länge - aber in entgegengesetzter Richtung - an die Spitze von $\overrightarrow{\mathrm a}$ ein, so erhält man vom Fuß von $\overrightarrow{\mathrm a}$ bis zur Spitze von $-\overrightarrow{\mathrm b}$ den Vektor $\overrightarrow{\mathrm a}-\overrightarrow{\mathrm b}=\overrightarrow{\mathrm d}$ .
  2) $|\vec c|$ und $|\vec d|$ zeichnerisch bestimmen
  Nun kannst du die Länge von $\vec c$ und $\vec d$ aus der Zeichnung ablesen:
  $|\vec c|\approx7{,}4$ und $|\vec d|\approx4{,}3$
  3) $\beta$ und $\gamma$ aus der Zeichnung ablesen
  Miss die Winkel $\beta$ und $\gamma$ ab:
  $\mathrm\beta\approx27{,}7^\circ$
  $\mathrm\gamma\approx53{,}1^\circ$
  4) $|\vec c|$ und $|\vec d|$ rechnerisch betimmen
  Verwende den Kosinussatz:
  $c^2=a^2+b^2-2{ab}\cdot\cos\left(120^\circ\right)\;\Rightarrow\;\;c=\left|\overrightarrow{c}\right|\approx7{,}454$
  $d^2=a^2+b^2-2{ab}\cdot\cos\left(60^\circ\right)\;\Rightarrow\;\; d=\left|\overrightarrow{d}\right|\approx4{,}331$
  5) $\beta$ und $\gamma$ rechnerisch bestimmen
  Für die Winkel $\mathrm\beta\;$ und $\gamma$ kann man sich wieder den Kosinussatz zu nutze machen:
  $\def\arraystretch{1.25} \begin{array}{l} b^2=a^2+c^2-2\mathrm{ac}\cdot\cos\left(\mathrm\beta\right)\\\;\;\Rightarrow\;\;\cos\left(\beta\right)=\frac{a^2+c^2-b^2}{2{ac}}\\\;\;\Rightarrow\;\;\mathrm\beta\approx27{,}693^\circ\end{array}$
  $\def\arraystretch{1.25} \begin{array}{l}b^2=a^2+d^2-2{ad}\cdot\cos\left(\gamma\right)\\\;\;\Rightarrow\;\;\cos\left(\gamma\right)=\frac{a^2+d^2-b^2}{2{ad}}\\\;\;\Rightarrow\;\;\mathrm\gamma\approx53{,}11^\circ\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $\left|\overrightarrow{\mathrm a}\right|=\mathrm a=4{,}2$ ; $\left|\overrightarrow{\mathrm b}\right|=\mathrm b=3{,}8$ ; $\mathrm\alpha=\sphericalangle\left(\overrightarrow{\mathrm a},\overrightarrow{\mathrm b}\right)=120^\circ$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
  1) Vektoren zeichnen
  Zeichne zunächst Vektor $\overrightarrow{\mathrm a}$ ein. Die Richtung ist egal. Entscheident ist die Länge von 4,2.
  Dann zeichnet man den Vektor $\overrightarrow{\mathrm b}$ im Winkel von $\mathrm\alpha=120^\circ$ gegen den Uhrzeigersinn an den Fuß von Vektor $\overrightarrow{\mathrm a}$ ein.
  Nun fehlen noch die Vektoren $\vec c$ und $\vec d$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit der selben Länge an die Spitze von Vektor $\overrightarrow{\mathrm a}$ so erhalten wir ein Parralelogramm, dass in der Diagonale den Vektor $\overrightarrow{\mathrm a}+\overrightarrow{\mathrm b}=\overrightarrow{\mathrm c}$ besitzt.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit der selben Länge, aber in der entgegengesetzten Richtung ein, so erhält man vom Fuß von $\overrightarrow{\mathrm a}$ bis zur Spitze von - $\overrightarrow{\mathrm b}$ den Vektor $\overrightarrow{\mathrm a}-\overrightarrow{\mathrm b}=\overrightarrow{\mathrm d}$ .
  2) $|\vec c|$ und zeichnerisch bestimmen
  Messe die Länge der Vektoren $\overrightarrow{\mathrm c}\;\mathrm{und}\;\overrightarrow{\mathrm d}$ ab.
  $\left|\overrightarrow{\mathrm c}\right|\approx4{,}0$
  $\left|\overrightarrow{\mathrm d}\right|\approx6{,}9$
  3) $\beta$ und $\gamma$ aus der Zeichnung ablesen
  Miss die Winkel $\beta$ und $\gamma$ ab:
  $\mathrm\beta\approx54{,}9^\circ$
  $\mathrm\gamma\approx28{,}3^\circ$
  4) $|\vec c|$ und $|\vec d|$ rechnerisch bestimmen
  Zunächst müssen wir die Winkel an der Spitze von a ermitteln. Durch den Z-Winkel sind unten 120° vorzufinden und oben 60°, da diese beiden Winkel insgesamt 180° ergeben müssen.
  Gesucht ist nun erst mal die Seite c. Um diese zu berechnen benutzen wir den Kosinussatz über die Seiten a und b und dem Winkel von 60°.
  Um d zu berechnen gehen wir genauso vor. Wir rechnen mit dem Kosinussatz über die Seiten a und b und dem Winkel von 120°.
  $\mathrm c²=\mathrm a²+\mathrm b²-2\mathrm{ab}\cdot\cos\left(60^\circ\right)\;\Rightarrow\;\;\mathrm c=\left|\overrightarrow{\mathrm c}\right|\approx4{,}015$
  $\mathrm d²=\mathrm a²+\mathrm b²-2\mathrm{ab}\cdot\cos\left(120^\circ\right)\;\Rightarrow\;\;\mathrm d=\left|\overrightarrow{\mathrm d}\right|\approx6{,}931$
  5) $\beta$ und $\gamma$ rechnerisch bestimmen
  Für die Winkel $\mathrm\beta\;\mathrm{und}\;\mathrm\gamma$ kann man sich wieder den Kosinussatz zu nutze machen.
  Hierfür rechnen wir erst b über c, a und dem Winkel $\mathrm\beta$ und formen dann nach $\cos\left(\mathrm\beta\right)$ um.
  Das selbe machen wir mit $\cos\left(\mathrm\gamma\right)$ .
  $\def\arraystretch{1.25} \begin{array}{l}\mathrm b²=\mathrm a²+\mathrm c²-2\mathrm{ac}\cdot\cos\left(\mathrm\beta\right)\\\;\;\Rightarrow\;\;\cos\left(\mathrm\beta\right)=\frac{\mathrm a²+\mathrm c²-\mathrm b²}{2\mathrm{ac}}\\\;\;\Rightarrow\;\;\mathrm\beta\approx55{,}05^\circ\end{array}$
  
  $\def\arraystretch{1.25} \begin{array}{l}\mathrm b²=\mathrm a²+\mathrm d²-2\mathrm{ad}\cdot\cos\left(\mathrm\gamma\right)\\\;\;\Rightarrow\;\;\cos\left(\mathrm\gamma\right)=\frac{\mathrm a²+\mathrm d²-\mathrm b²}{2\mathrm{ad}}\\\;\;\Rightarrow\;\;\mathrm\gamma\approx28{,}346^\circ\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $\left|\overrightarrow{\mathrm a}\right|=\mathrm a=4{,}7$ ; $\left|\overrightarrow{\mathrm b}\right|=\mathrm b=3{,}2$ ; $\mathrm\alpha=\sphericalangle\left(\overrightarrow{\mathrm a},\overrightarrow{\mathrm b}\right)=250^\circ$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
  1) Vektoren zeichnen
  Zeichne zunächst Vektor $\overrightarrow{\mathrm a}$ ein. Richtung ist egal. Entscheident ist die Länge von 4,7.
  Dann zeichnet man den Vektor $\overrightarrow{\mathrm b}$ im Winkel von $\mathrm\alpha=250^\circ$ gegen den Uhrzeigersinn an den Fuß von Vektor $\overrightarrow{\mathrm a}$ ein.
  Nun fehlen noch die Vektoren $\vec c$ und $\vec d$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit der selben Länge an die Spitze von Vektor $\overrightarrow{\mathrm a}$ so erhalten wir ein Parralelogramm, dass in der Diagonale den Vektor $\overrightarrow{\mathrm a}+\overrightarrow{\mathrm b}=\overrightarrow{\mathrm c}$ besitzt.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit der selben Länge, aber in der entgegengesetzten Richtung ein, so erhält man vom Fuß von $\overrightarrow{\mathrm a}$ bis zur Spitze von - $\overrightarrow{\mathrm b}$ den Vektor $\overrightarrow{\mathrm a}-\overrightarrow{\mathrm b}=\overrightarrow{\mathrm d}$ .
  2) $\overrightarrow{\mathrm c}$ und $\overrightarrow{\mathrm d}$ zeichnerisch bestimmen
  Messe die Länge der Vektoren $\overrightarrow{\mathrm c}\;\mathrm{und}\;\overrightarrow{\mathrm d}$ ab.
  $\left|\overrightarrow{\mathrm c}\right|\approx4{,}7$
  $\left|\overrightarrow{\mathrm d}\right|\approx6{,}5$
  3) $\beta$ und $\gamma$ aus der Zeichnung ablesen
  Miss die Winkel $\beta$ und $\gamma$ ab:
  $\mathrm\beta\approx39{,}8^\circ$
  $\mathrm\gamma\approx27{,}4^\circ$
  4) $|\vec c|$ und $|\vec d|$ rechnerisch bestimmen
  Zunächst müssen wir die Winkel an der Spitze von a ermitteln.
  Dafür brauchen wir den Winkel den b im Uhrzeigesinn von a entfernt ist. Dieser beträgt $\mathrm\alpha-180^\circ=70^\circ$ .
  Durch den Z-Winkel sind nun an der Spitze von a unten 70° vorzufinden und oben 110°, da diese beiden Winkel insgesamt 180° ergeben müssen.
  Gesucht ist nun erst mal die Seite c. Um diese zu berechnen benutzen wir den Kosinussatz über die Seiten a und b und dem Winkel von 70°.
  Um d zu berechnen gehen wir genauso vor. Wir rechnen mit dem Kosinussatz über die Seiten a und b und dem Winkel von 110°.
  $\mathrm c²=\mathrm a²+\mathrm b²-2\mathrm{ab}\cdot\cos\left(70^\circ\right)\;\Rightarrow\;\;\mathrm c=\left|\overrightarrow{\mathrm c}\right|\approx4{,}695$
  $\mathrm d²=\mathrm a²+\mathrm b²-2\mathrm{ab}\cdot\cos\left(110^\circ\right)\;\Rightarrow\;\;\mathrm d=\left|\overrightarrow{\mathrm d}\right|\approx6{,}528$
  5) $\beta$ und $\gamma$ rechnerisch bestimmen
  Für die Winkel $\mathrm\beta\;\mathrm{und}\;\mathrm\gamma$ kann man sich wieder den Kosinussatz zu nutze machen.
  Hierfür rechnen wir erst b über c, a und dem Winkel $\mathrm\beta$ und formen dann nach $\cos\left(\mathrm\beta\right)$ um.
  Das selbe machen wir mit $\cos\left(\mathrm\gamma\right)$ .
  $\def\arraystretch{1.25} \begin{array}{l}\mathrm b²=\mathrm a²+\mathrm c²-2\mathrm{ac}\cdot\cos\left(\mathrm\beta\right)\\\;\;\Rightarrow\;\;\cos\left(\mathrm\beta\right)=\frac{\mathrm a²+\mathrm c²-\mathrm b²}{2\mathrm{ac}}\\\;\;\Rightarrow\;\;\mathrm\beta\approx39{,}828^\circ\end{array}$
  
  $\def\arraystretch{1.25} \begin{array}{l}\mathrm b²=\mathrm a²+\mathrm d²-2\mathrm{ad}\cdot\cos\left(\mathrm\gamma\right)\\\;\;\Rightarrow\;\;\cos\left(\mathrm\gamma\right)=\frac{\mathrm a²+\mathrm d²-\mathrm b²}{2\mathrm{ad}}\\\;\;\Rightarrow\;\;\mathrm\gamma\approx27{,}427^\circ\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $\left|\overrightarrow{\mathrm a}\right|=\mathrm a=3{,}5$ ; $\left|\overrightarrow{\mathrm b}\right|=\mathrm b=4{,}2$ ; $\mathrm\alpha=\sphericalangle\left(\overrightarrow{\mathrm a},\overrightarrow{\mathrm b}\right)=290^\circ$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
  1) Vektoren zeichnen
  Zeichne zunächst Vektor $\overrightarrow{\mathrm a}$ ein. Richtung ist egal. Entscheident ist die Länge von 3,5.
  Dann zeichnet man den Vektor $\overrightarrow{\mathrm b}$ im Winkel von $\mathrm\alpha=290^\circ$ gegen den Uhrzeigersinn an den Fuß von Vektor $\overrightarrow{\mathrm a}$ ein.
  Nun fehlen noch die Vektoren $\vec c$ und $\vec d$ , welche durch Vektoraddition bzw. Vektorsubtraktion entstehen.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit der selben Länge an die Spitze von Vektor $\overrightarrow{\mathrm a}$ so erhalten wir ein Parralelogramm, dass in der Diagonale den Vektor $\overrightarrow{\mathrm a}+\overrightarrow{\mathrm b}=\overrightarrow{\mathrm c}$ besitzt.
  Zeichnet man Vektor $\overrightarrow{\mathrm b}$ nun im selben Winkel und mit der selben Länge, aber in der entgegengesetzten Richtung ein, so erhält man vom Fuß von $\overrightarrow{\mathrm a}$ bis zur Spitze von - $\overrightarrow{\mathrm b}$ den Vektor $\overrightarrow{\mathrm a}-\overrightarrow{\mathrm b}=\overrightarrow{\mathrm d}$ .
  2) $|\vec c|$ und $|\vec d|$ zeichnerisch bestimmen
  Messe die Länge der Vektoren $\overrightarrow{\mathrm c}\;\mathrm{und}\;\overrightarrow{\mathrm d}$ ab.
  $\left|\overrightarrow{\mathrm c}\right|\approx6{,}3$
  $\left|\overrightarrow{\mathrm d}\right|\approx4{,}5$
  3) $\beta$ und $\gamma$ aus der Zeichnung ablesen
  Miss die Winkel $\beta$ und $\gamma$ ab:
  $\mathrm\beta\approx38{,}6^\circ$
  $\mathrm\gamma\approx62{,}3^\circ$
  4) $|\vec c|$ und $|\vec d|$ rechnerisch bestimmen
  $\overrightarrow{\mathrm c}$ und $\overrightarrow{\mathrm d}$ rechnerisch bestimmen mit Kosinussatz
  Zunächst müssen wir die Winkel an der Spitze von a ermitteln.
  Dafür brauchen wir den Winkel den b im Uhrzeigesinn von a entfernt ist. Dieser beträgt $\mathrm\alpha-180^\circ=110^\circ$ .
  Durch den Z-Winkel sind nun an der Spitze von a unten 110° vorzufinden und oben 70°, da diese beiden Winkel insgesamt 180° ergeben müssen.
  Gesucht ist nun erst mal die Seite c. Um diese zu berechnen benutzen wir den Kosinussatz über die Seiten a und b und dem Winkel von 110°.
  Um d zu berechnen gehen wir genauso vor. Wir rechnen mit dem Kosinussatz über die Seiten a und b und dem Winkel von 70°.
  $\mathrm c²=\mathrm a²+\mathrm b²-2\mathrm{ab}\cdot\cos\left(110^\circ\right)\;\Rightarrow\;\;\mathrm c=\left|\overrightarrow{\mathrm c}\right|\approx6{,}32$
  $\mathrm d²=\mathrm a²+\mathrm b²-2\mathrm{ab}\cdot\cos\left(70^\circ\right)\;\Rightarrow\;\;\mathrm d=\left|\overrightarrow{\mathrm d}\right|\approx4{,}454$
  5) $\beta$ und $\gamma$ rechnerisch bestimmen
  Für die Winkel $\mathrm\beta\;\mathrm{und}\;\mathrm\gamma$ kann man sich wieder den Kosinussatz zu nutze machen.
  Hierfür rechnen wir erst b über c, a und dem Winkel $\mathrm\beta$ und formen dann nach $\cos\left(\mathrm\beta\right)$ um.
  Das selbe machen wir mit $\cos\left(\mathrm\gamma\right)$ .
  $\def\arraystretch{1.25} \begin{array}{l}\mathrm b²=\mathrm a²+\mathrm c²-2\mathrm{ac}\cdot\cos\left(\mathrm\beta\right)\\\;\;\Rightarrow\;\;\cos\left(\mathrm\beta\right)=\frac{\mathrm a²+\mathrm c²-\mathrm b²}{2\mathrm{ac}}\\\;\;\Rightarrow\;\;\mathrm\beta\approx38{,}642^\circ\end{array}$
  
  $\def\arraystretch{1.25} \begin{array}{l}\mathrm b²=\mathrm a²+\mathrm d²-2\mathrm{ad}\cdot\cos\left(\mathrm\gamma\right)\\\;\;\Rightarrow\;\;\cos\left(\mathrm\gamma\right)=\frac{\mathrm a²+\mathrm d²-\mathrm b²}{2\mathrm{ad}}\\\;\;\Rightarrow\;\;\mathrm\gamma\approx62{,}397^\circ\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
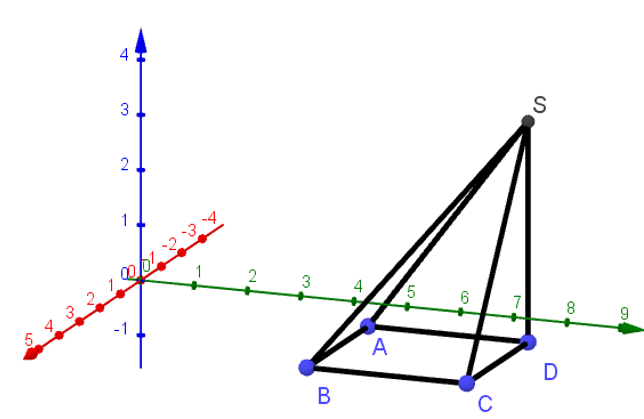
Eine Pyramide ABCDS hat eine quadratische Grundfläche ABCD, die parallel zur $x_1x_2$ -Ebene ist. Jede Seite des Quadrats ist 3 LE lang. Der linke, hintere Eckpunkt A liegt bei (-2|3,5|-1) und die Spitze S liegt senkrecht 4 LE über dem Punkt D.
1. Zeichne die Pyramide in ein Koordinatensystem und gib die Koordinaten der übrigen Eckpunkte B,C D und S an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreidimensionales Koordinatensystem
  Koordinatensystem
  Da die quadratische Grundfläche parallel zur $x_1x_2$ -Ebene ist und A die linke, hintere Ecke ist, kannst du für den Punkt B von A aus drei Längeneinheiten in $x_1$ -Richtung gehen und für den Punkt D von A aus drei Längeneinheiten in $x_2$ -Richtung. Für C gehst du dann z.B von B aus drei Längeneinheiten in $x_2$ -Richtung. Die Spitze befindet sich senkrecht über D, also gehst du von D aus vier Längeneinheiten in $x_3$ -Richtung.
  Koordinaten
  Für die Punkte ergeben sich somit die Koordinaten $B(1|3{,}5|-1), C(1|6{,}5|-1), D(-2|6{,}5|-1)$ und $S(-2|6{,}5|3)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme das Volumen der Pyramide.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Das Volumen einer Pyramide kann z.B. berechnet werden mit $V=\frac 1 3\cdot G\cdot h$
  mit quadratischer Grundfläche also $V=\frac 1 3\cdot a^2\cdot h$
  Das Quadrat hat eine Seitenlänge von 3 LE und die Pyramide ist 4 LE hoch:
  $V=\frac 1 3 \cdot 3^2\cdot 4=12$ (VE)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉