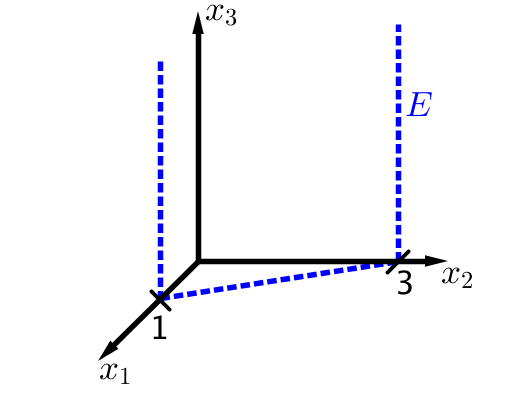
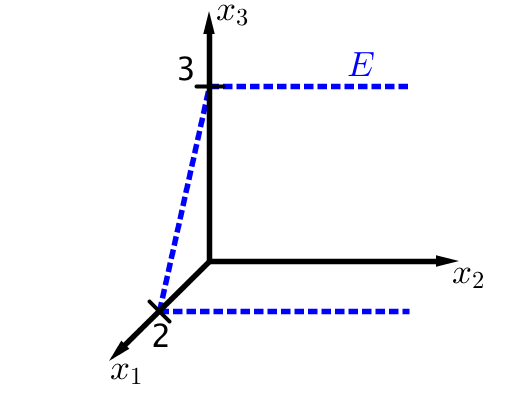
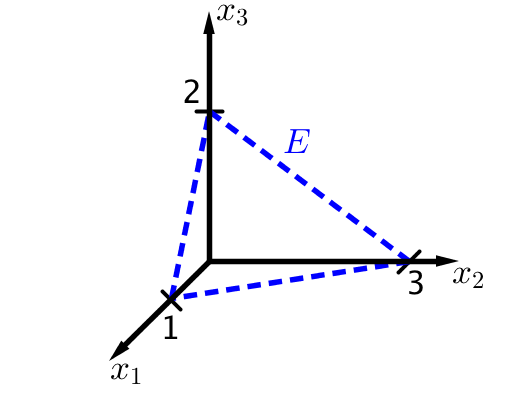
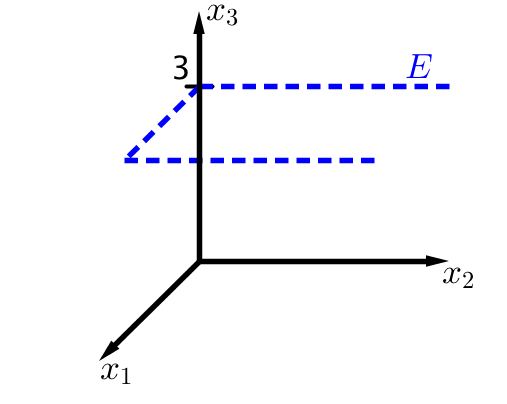
In den folgenden Bildern ist je eine Ebene E dargestellt. Stelle die dargestellte Ebene in Parameterform auf.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?
In den folgenden Bildern ist je eine Ebene E dargestellt. Stelle die dargestellte Ebene in Parameterform auf.