Langfristige Klimaprognosen prophezeien auch für unser Wetter zunehmende Sturmschäden, von denen auch Bahnstrecken betroffen sein können.

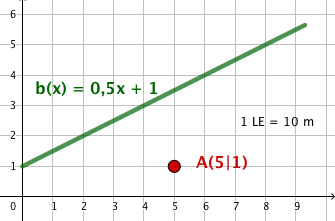
Neben der Bahnlinie steht im Punkt eine hohe Fichte.
Ob sie für die Bahnstrecke eine Gefahr darstellt?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Tipp: Der Baum stellt dann eine Gefahr für Züge dar, wenn sein Abstand zur Bahn kleiner ist als seine Höhe.
Bei einem Sturm könnte er entwurzelt werden und auf die Bahnstrecke fallen.
Die drei möglichen unterschiedlichen Lösungswege für die gestellte Aufgabe:
Berechnung der Lösung als Extremwertaufgabe:Welcher Punkt der Funktion kommt dem Punkt am nächsten?
Konstruktion und/oder Berechnung des Fußpunktes des Lotes von auf die Gerade und Bestimmung seines Abstands zu .
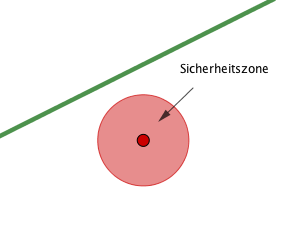
Betrachtung der Sicherheitszone des gegebenen Baumes und ihre Lage zur Bahnstrecke.
Bei dieser Aufgabe sollst du den Abstand eines Punktes von einer Geraden als Extremwertaufgabe berechnen und das Ergebnis in seiner praktischen Bedeutung eines notwendigen Sicherheitsabstandes deuten.
Hinweis:
Die benötigten Funktionen werden nur mit den Maßzahlen der Größen (ohne ihre Maßeinheit) erstellt.
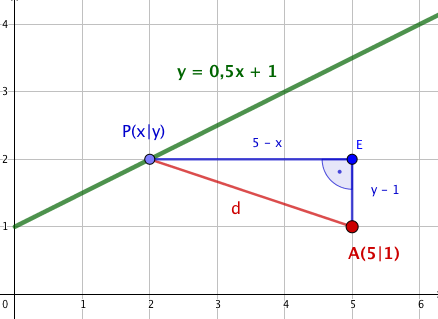
Der verschiebbare Punkt gehört zur Funktion . Dies ist die Nebenbedingung für die Zielfunktion .
Die Nebenbedingung in die Zielfunktion eingesetzt ergibt:
Beachte, dass die Zielfunktion jetzt nur noch von der einen Variablen x abhängt.
Fasse zusammen.
Beachte: Für denselben - noch zu berechnenden x-Wert - für den ein Minimum wird, wird auch der Term minimal.
Quadriere deshalb die Gleichung.
Bilde die 1. Ableitung von .
Setze gleich Null und löse die Gleichung nach x auf.
liefert ein kleinstes , wenn die 2. Ableitung positiv ist.
Setze in die Nebenbedingung ein.
ist der gesuchte Punkt auf der Bahnstrecke mit minimalem Abstand zu Punkt .
Setze die Koordinaten von in ein (nicht in ).
Da der Baum nur hoch ist, kann er - vorausgesetzt, ein Sturm trägt einzelne Äste nicht noch weiter - auch dann, wenn er entwurzelt umfällt, die Bahnstrecke nicht gefährden.
Im Applet kannst du den Punkt P verschieben und den jeweiligen Abstand zu ablesen.
Alternative Lösung
Der als Extremwert berechnete Punkt mit minimalem Abstand von zur Geraden kann auch als Lotfußpunkt des Lotes von auf die Gerade konstruiert oder berechnet werden.
Die Konstruktion des Lotfußpunktes:
Der Kreis um mit schneidet die Gerade in und .
Die Kreise um und mit schneiden sich in und .
Die Geraden und schneiden sich im Lotfußpunkt .
Die Konstruktion kann im obigen Applet schrittweise nachvollzogen werden. Benutze dazu die Konstruktionsleiste im unteren Teil des Applets.
Die Berechnung des Lotfußpunktes:
Schneide die Gerade mit der dazu senkrechten Geraden durch den Punkt .
Lies die Steigung für die Gerade b aus der Funktionsgleichung ab.
Für die zu senkrechte Steigung gilt:.
Berechne .
Stelle die Gleichung für die Lotgerade durch auf.
Benutze die Formel
.
Multipliziere mit dem Nenner und löse nach y auf.
Schneide mit indem du die Funktionsterme gleichsetzt.
Setze in ein.
ist der gesuchte Lotfußpunkt.
Ergänzende Betrachtung der Aufgabenstellung
Die Kreisfläche um mit Radius (= Baumhöhe) beschreibt die Sicherheitszone falls der Baum bei Sturm umstürzen würde.
Da in der Aufgabenstellung lediglich gefragt wird, ob der Baum für die Bahnstrecke "gefährlich" sein könnte, genügt es, rechnerisch oder graphisch nachzuweisen, ob der Sicherheitskreis die Gerade schneidet oder nicht.
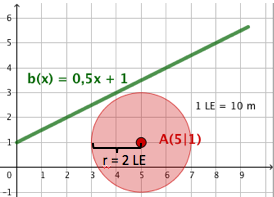
Die graphische Lösung:
Die Kreisfläche um mit Radius erreicht die Bahnstrecke nicht.
Der rechnerische Nachweis, dass der Kreis die Gerade nicht schneidet:
Benutze zum Schnitt die Kreisgleichung
für einen Kreis um den Punkt mit Radius und die Geradengleichung .
Die Kreisgleichung:
Die Geradengleichung:
Setze in die Kreisgleichung ein.Fasse die entstehende quadratische Gleichung zusammen.
Gib die Diskriminante an.
Da die Diskriminante negativ ist, schneiden sich der "Sicherheitskreis" um und die Bahnstrecke nicht.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?
