Komplexere Anwendungsaufgaben mit Extremwertproblemen
Absolut extrem! Mit diesen Anwendungsaufgaben lernst du, Extremwertprobleme zu lösen und vertiefst dein Wissen.
- 1
Ein Versandhaus verschickt seine Artikel weltweit als Päckchen der Deutschen Post AG (DHL) mit deren Gebührenordnung für quaderförmige Päckchen international. Aus verpackungstechnischen Gründen des Versandhauses ist die Länge einer Seite mit festgelegt.
Die Päckchen müssen Mindestmaße einhalten.
Für die Maximalgröße ist beim Tarif Päckchen international die Summe aus Länge, Breite und Höhe begrenzt und keine der Seiten darf länger als sein.
Das Maximalgewicht für Päckchen ist .
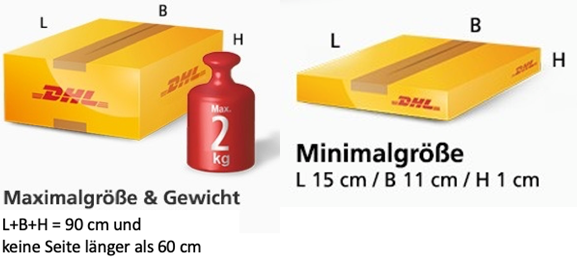
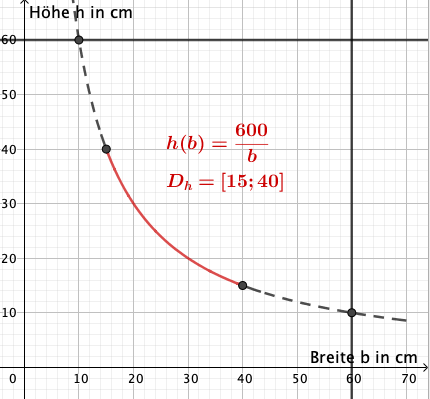
Bestimme für ein Volumen von den Zusammenhang von Breite und Höhe.
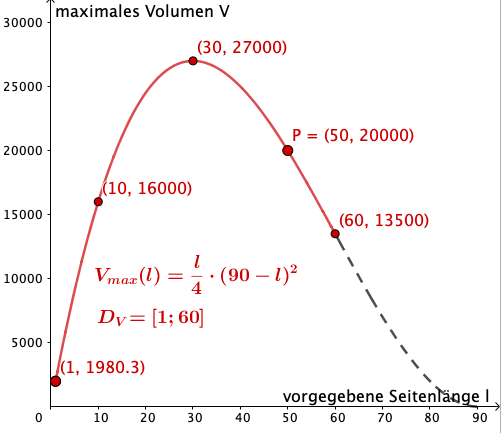
Wie groß ist das für eine vorgegebene Seitenlänge von erreichbare maximale Volumen eines Päckchens?
Verallgemeinere die Teilaufgabe b) indem du zeigst, dass für jede vorgegebene zugelassene Päckchenseitenlänge das Päckchen mit dem größtmöglichen Volumen einen quadratischen Querschnitt besitzt.
Gibt die Funktion für das maximale Volumen eines Päckchens in Abhängigkeit von einer vorgegebenen zulässigen Päckchenseitenlänge an.
- 2
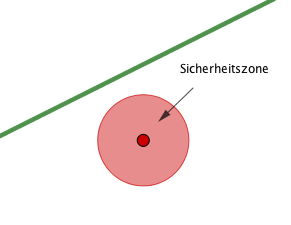
Langfristige Klimaprognosen prophezeien auch für unser Wetter zunehmende Sturmschäden, von denen auch Bahnstrecken betroffen sein können.

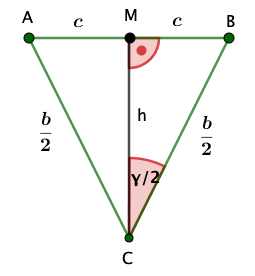
Neben der Bahnlinie steht im Punkt eine hohe Fichte.
Ob sie für die Bahnstrecke eine Gefahr darstellt?
- 3
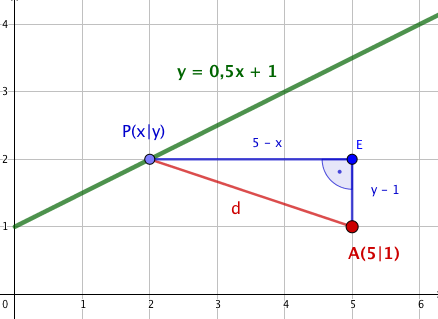
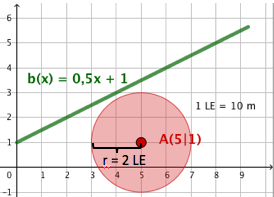
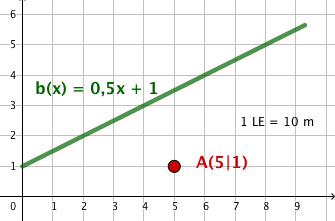
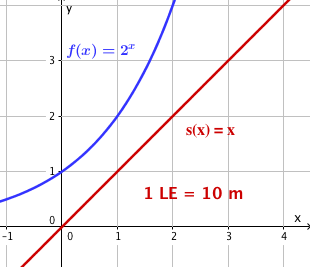
Zwischen einer Straße und einem Bach soll als Hochwasserschutz ein Damm errichtet werden.
Aus technischen Gründen ist dies aber nur möglich, wenn der Bach der Straße auf höchstens 5 m nahekommt.
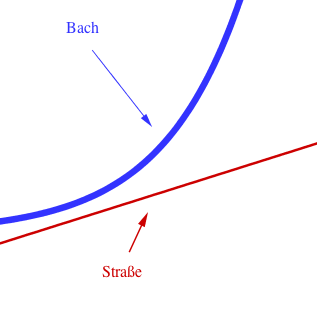
Berechne, ob der Schutzdamm bei dem gegebenen Geländeplan (1LE = 10 m) gebaut werden kann, wenn der Bach dem Graphen der Funktion und die Straße dem Graphen der Funktion folgen.
- 4
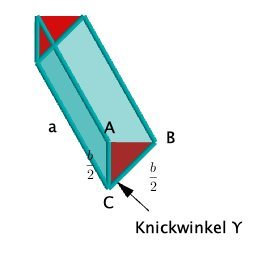
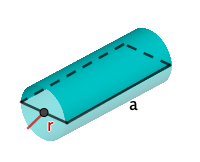
Aus einer rechteckigen Blechtafel der Länge und der Breite soll eine Dachrinne (Länge ) hergestellt werden, die maximales Wasservolumen aufnehmen kann.
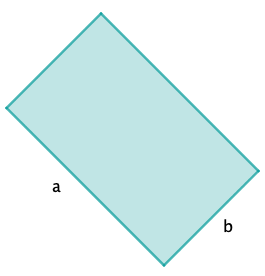
Die Blechtafel wird V-förmig gebogen.
Welcher "Knickwinkel" ist zu wählen? Welches maximale Wasservolumen ergibt sich?
Die Blechtafel wird rechteckig gebogen. Wie ist das Blech zu biegen, damit sich ein maximales Wasservolumen ergibt?
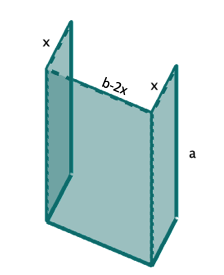
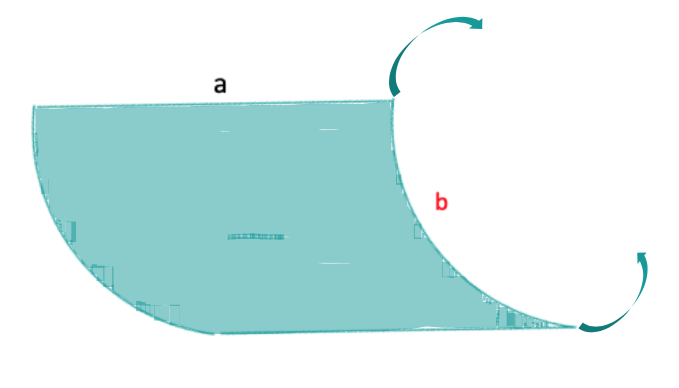
Die Blechtafel wird halbkreisförmig gebogen. Welches Wasservolumen ergibt sich?
Vergleiche die Ergebnisse der drei Teilaufgaben.
- 5
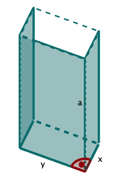
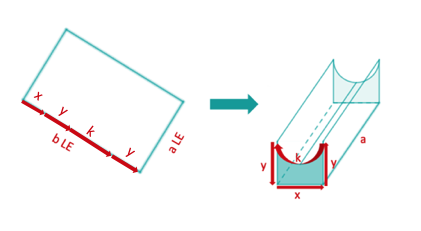
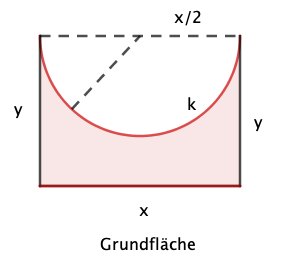
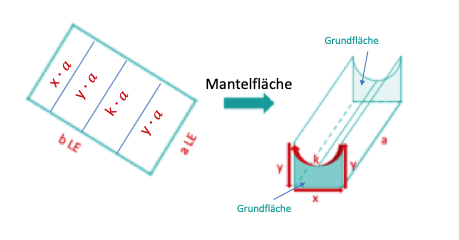
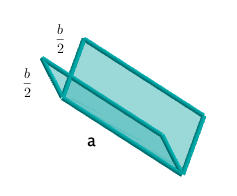
Eine rechteckige Blechtafel mit den Seitenlängen und wird zu einem quaderförmigen Gegenstand so geknickt und gebogen, dass dieser an der oberen Mantelfläche halbkreisförmig eingedellt ist. Der Körper sei durch seine beiden Grundflächen abgeschlossen. (Siehe die nachfolgende Skizze.)
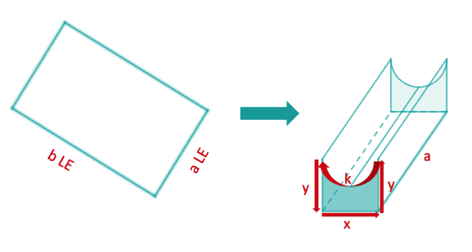
Bestimme das größtmögliche Volumen eines solchen Körpers.
Bestimme seine Mantelfläche.
Berechne die größtmögliche Oberfläche des Körpers.
Welche Kantenmaße hat dieser größtmögliche Körper für und ?
- 6
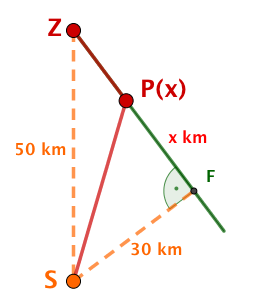
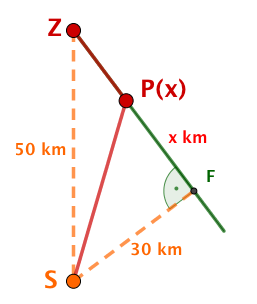
Eine Wüstenrallye gewinnt
bei einer "traditionellen" Rallye, wer als Erster am Ziel ankommt,
bei einer "alternativen" Rallye, wer den geringsten Bezinverbrauch hat.
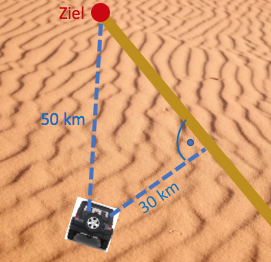
Vor dem Start steht das Team vor folgendem Problem:
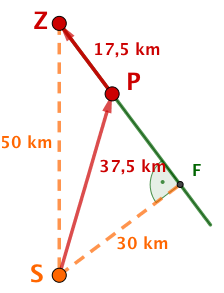
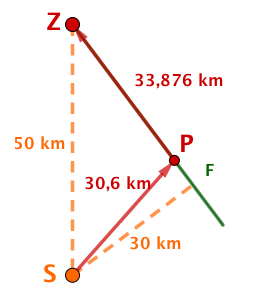
Der Startort liegt mitten in der Wüste und ist vom Zielort entfernt.
Der direkte Weg zum Ziel führt durch den Wüstensand. Dort kann das Fahrzeug des Teams eine Durchschnittsgeschwindigkeit von bei einem Durchschnittsverbrauch von erreichen.
In Entfernung vom Standort führt allerdings eine schnurgerade Karawanenstraße zum Zielort. Dort könnte das Fahrzeug eine Durchschnittsgeschwindigkeit von bei einem Durchschnittsverbrauch von nur fahren.
Welche Route wird das Team bei der traditionellen Rallye wählen?
Welche Route wird das Team bei einer alternativen Rallye wählen, wenn es jede Route zwischen Startort, Straße und Zielort fahren kann? Nach welcher Zeit bzw. mit welchem Verbrauch wird es jeweils das Ziel erreichen?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?