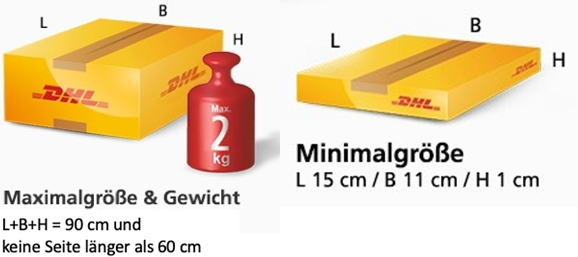
Ein Versandhaus verschickt seine Artikel weltweit als Päckchen der Deutschen Post AG (DHL) mit deren Gebührenordnung für quaderförmige Päckchen international. Aus verpackungstechnischen Gründen des Versandhauses ist die Länge einer Seite mit festgelegt.
Die Päckchen müssen Mindestmaße einhalten.
Für die Maximalgröße ist beim Tarif Päckchen international die Summe aus Länge, Breite und Höhe begrenzt und keine der Seiten darf länger als sein.
Das Maximalgewicht für Päckchen ist .
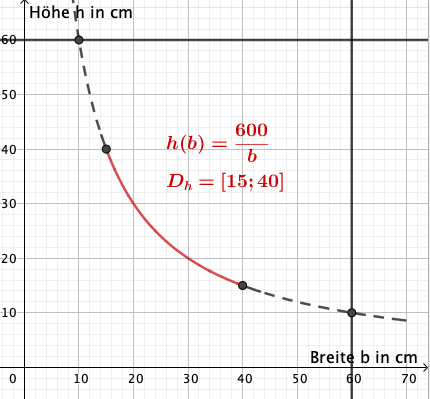
Bestimme für ein Volumen von den Zusammenhang von Breite und Höhe.
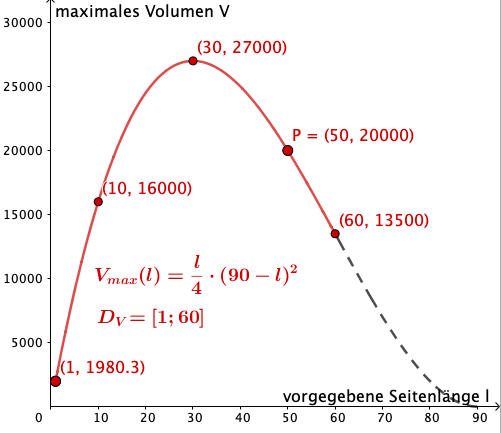
Wie groß ist das für eine vorgegebene Seitenlänge von erreichbare maximale Volumen eines Päckchens?
Verallgemeinere die Teilaufgabe b) indem du zeigst, dass für jede vorgegebene zugelassene Päckchenseitenlänge das Päckchen mit dem größtmöglichen Volumen einen quadratischen Querschnitt besitzt.
Gibt die Funktion für das maximale Volumen eines Päckchens in Abhängigkeit von einer vorgegebenen zulässigen Päckchenseitenlänge an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?