Eine Wüstenrallye gewinnt
bei einer "traditionellen" Rallye, wer als Erster am Ziel ankommt,
bei einer "alternativen" Rallye, wer den geringsten Bezinverbrauch hat.
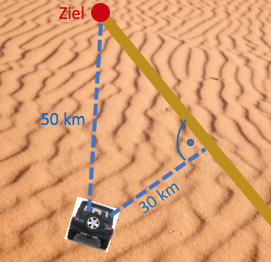
Vor dem Start steht das Team vor folgendem Problem:
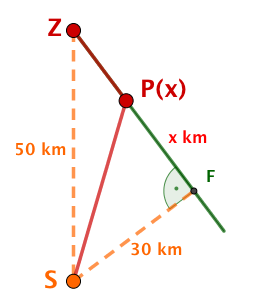
Der Startort liegt mitten in der Wüste und ist vom Zielort entfernt.
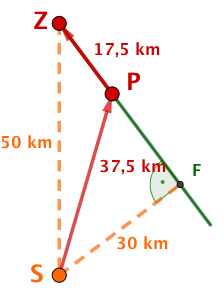
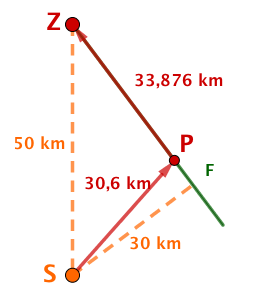
Der direkte Weg zum Ziel führt durch den Wüstensand. Dort kann das Fahrzeug des Teams eine Durchschnittsgeschwindigkeit von bei einem Durchschnittsverbrauch von erreichen.
In Entfernung vom Standort führt allerdings eine schnurgerade Karawanenstraße zum Zielort. Dort könnte das Fahrzeug eine Durchschnittsgeschwindigkeit von bei einem Durchschnittsverbrauch von nur fahren.
Welche Route wird das Team bei der traditionellen Rallye wählen?
Welche Route wird das Team bei einer alternativen wählen, wenn es jede Route zwischen Startort, Straße und Zielort fahren kann? Nach welcher Zeit bzw. mit welchem Verbrauch wird es jeweils das Ziel erreichen?
