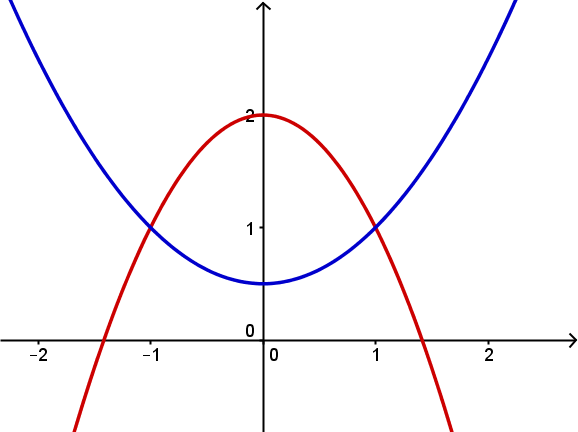
Die Graphen der Funktionen und schließen eine Fläche mit dem Inhalt A ein.
Schraffiere diese Fläche und berechne A.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?

Die Graphen der Funktionen und schließen eine Fläche mit dem Inhalt A ein.
Schraffiere diese Fläche und berechne A.