Die beiden Skizzen zeigen einen Quader und einen Würfel mit deren Abmessungen.
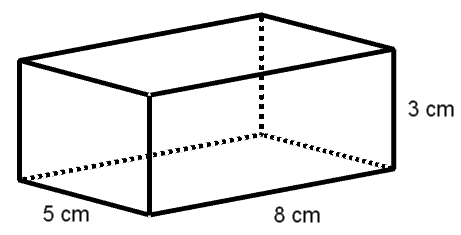
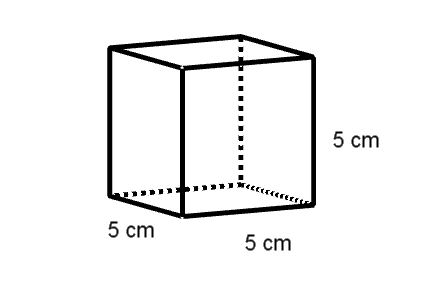
Welcher dieser beiden Körper hat den größeren Oberflächeninhalt?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt
Tipp: Wenn du dir nicht sicher bist, wie die Formel für den Oberflächeninhalt eines Quaders lautet, überlege dir, welche Seitenflächen gleich sind und wie du diese jeweils berechnen kannst.
Oberflächeninhalt
Der Oberflächeninhalt beider Körper wird hier berechnet und anschließend verglichen.
Oberfläche des Quaders
Die Formel zur Berechnung der Oberfläche eines Quaders lautet:
Für den Quader links sind:
Diese Werte werden in die Formel eingesetzt:
Der Oberflächeninhalt des Quaders beträgt also
Oberfläche des Würfels
Für den Würfel rechts ist die Kantenlänge . Die Fläche einer Seite kann wie folgt berechnet werden:
Da bei einem Würfel alle Seitenflächen gleich groß sind, ergibt sich für die Oberfläche:
Der Oberflächeninhalt des Würfels beträgt also .
Vergleich
Der Oberflächeninhalt des linken Quaders ist größer als der Oberflächeninhalt des rechten Würfels .
Hast du eine Frage oder Feedback?
Berechne die Oberfläche des Würfels mit der Formel und die des Quaders mit .
Welcher dieser beiden Körper hat das größere Volumen?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Räumliche Figuren
Volumen
Das Volumen der beiden Körper wird hier berechnet, um beide Volumina vergleichen zu können.
Volumen des Quaders
Das Volumen eines Quaders lässt sich mit der folgenden Formel berechnen:
Aus der Skizze, oder aus Aufgabe (a), kannst du folgende Werte ablesen:
cm
cm
cm
Diese Werte kannst du nun in die Formel einsetzen:
Das Volumen des Quaders links beträgt also .
Volumen des Würfels
Das Volumen eines Würfels lässt sich mit der folgenden Formel berechen:
Der Würfel aus der Skizze links hat eine Kantenlänge cm. Diesen Wert kannst du nun in die Formel einsetzen:
Das Volumen des Würfels rechts beträgt also .
Erkenntnis
Der Quader hat somit ein kleineres Volumen als der Würfel , obwohl der Oberflächeninhalt des Quaders größer ist als der Oberflächeninhalt des Würfels .
Eine Größere Oberfläche bedeutet also nicht zwingend ein größeres Volumen!
Hast du eine Frage oder Feedback?
Berechne das Volumen des Würfels mit der Formel und das Volumen des Quaders mit .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
