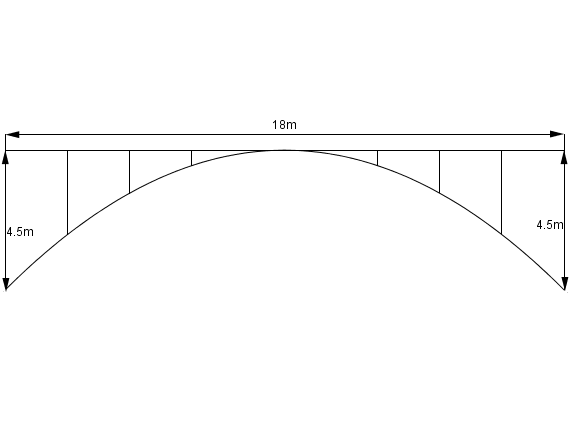
Für eine 18m lange Brücke werden in 2m Abstand Stützpfeiler benötigt. Diese verbinden den horizontalen Laufweg mit dem parabelförmigen Bogen unterhalb der Brücke. Die Höhe der beiden äußersten Stützpfeiler beträgt 4,5m.
Berechne die Länge aller Pfeiler.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
