Anwendungsaufgaben zu quadratischen Funktionen

Wie gut kennst du dich mit quadratischen Funktionen aus? Wiederhole wichtige Grundlagen und vertiefe dein Verständnis mit diesen Anwendungsaufgaben.

1
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
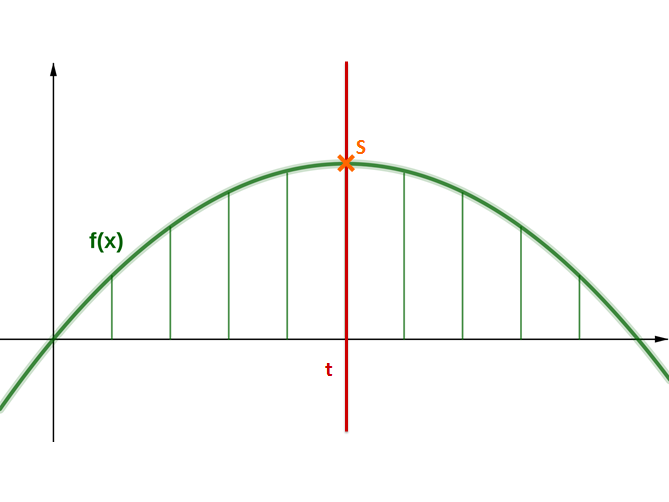
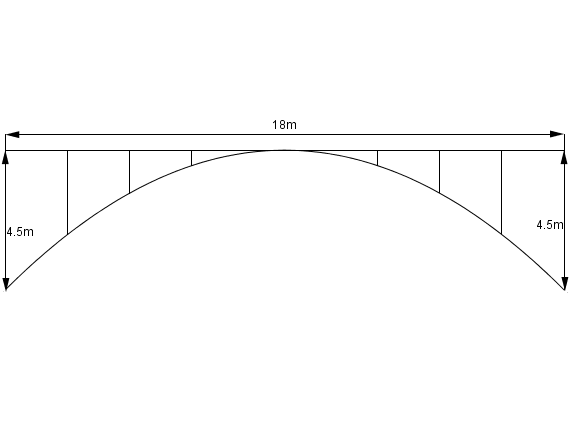
Für eine 18m lange Brücke werden in 2m Abstand Stützpfeiler benötigt. Diese verbinden den horizontalen Laufweg mit dem parabelförmigen Bogen unterhalb der Brücke. Die Höhe der beiden äußersten Stützpfeiler beträgt 4,5m.
Berechne die Länge aller Pfeiler.
2
Die Firma Habmichgern soll eine Brücke planen. Die Länge soll $60\,\mathrm m$ betragen.
Der Chef der Firma bittet dich, mithilfe der folgenden Funktionsgleichung die maximale Höhe der Brücke zu berechnen.
$f(x)=-\ 0{,}02\cdot x^2+1{,}2\cdot x$
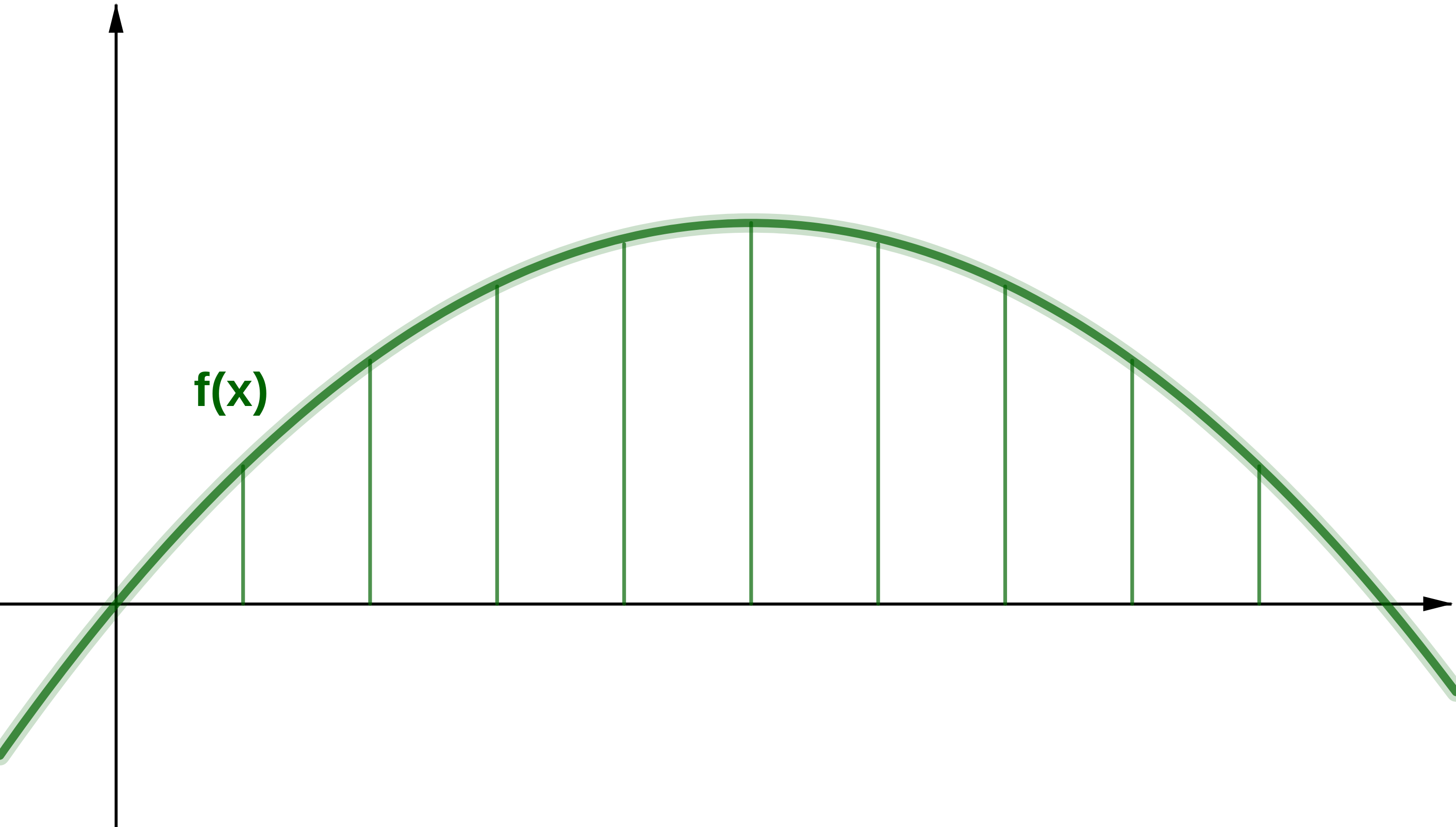m
3
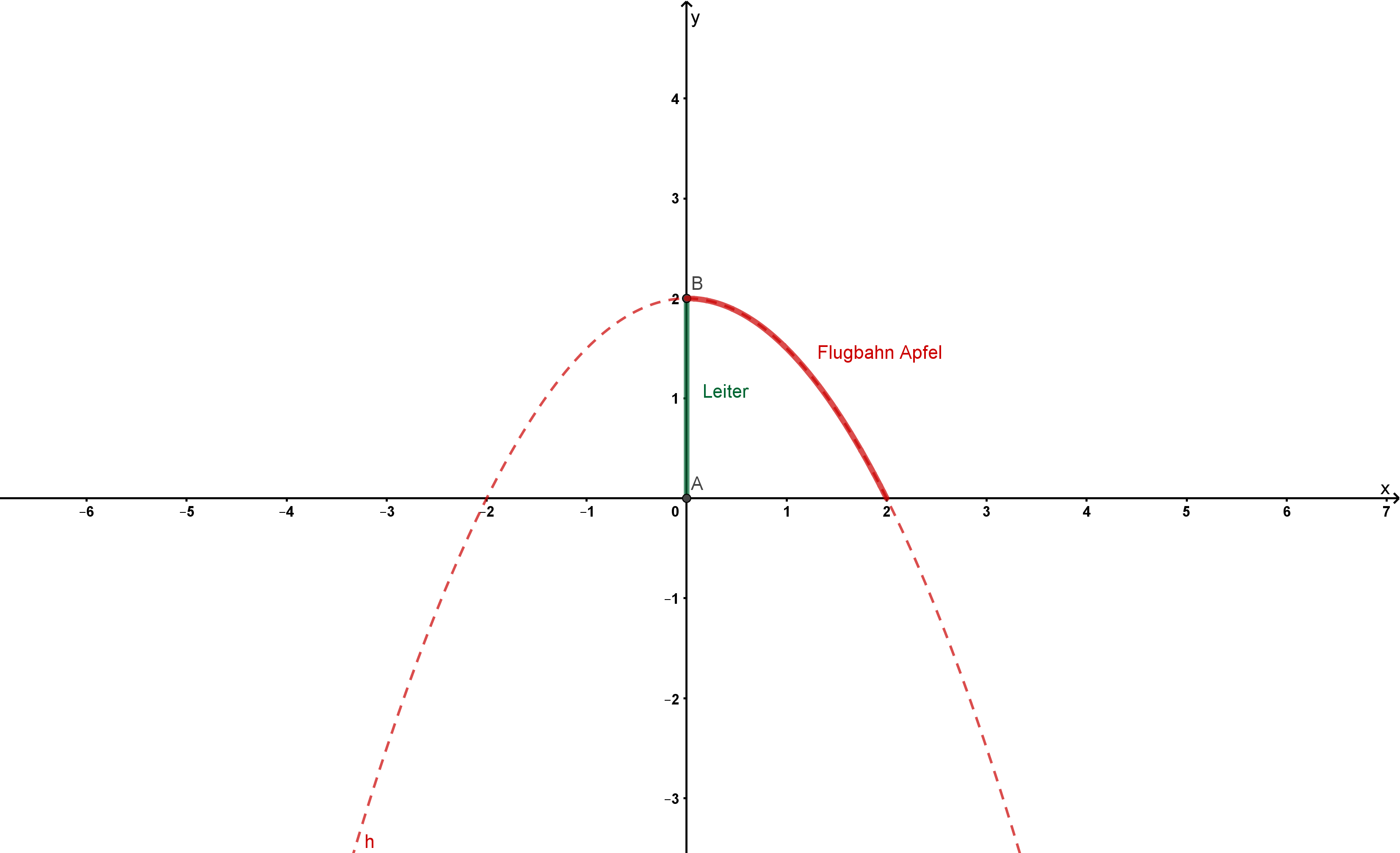
Es ist Erntezeit und Nico möchte Äpfel pflücken. Da er zu klein ist, um an die Äpfel zu kommen, stellt er eine Leiter unter den Apfelbaum. Von der Leiter aus will er die Äpfel in einen Korb werfen, der auf dem Boden ein Stück von der Leiter entfernt steht.
Nico wirft aus einer Höhe von $2\ \text{m}$ . Nico kennt die Newton'schen Gesetze der Gravitation und weiß somit, dass die Flughöhe $h$ des Apfels in Abhängigkeit von der Entfernung $x$ zur Leiter beschrieben werden kann durch $h=-\frac{1}{2\ \text{m}}x^2+2$ .
1. Skizziere die Flugbahn des Apfels mithilfe einer Parabel in ein Koordinatensystem.
2. Berechne, mit wieviel Meter Abstand zur Leiter Nico den Korb positionieren muss, damit er genau in den Korb trifft.
  m
3. In Teilaufgabe b) erhältst du zwei Lösungen. Wieso ergibt nur eine Sinn?
4
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
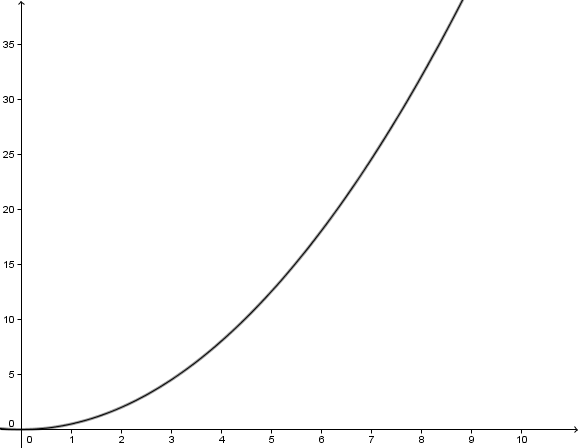
Ein biologischer Versuch zeigt folgende Messwerte bei der Untersuchung einer Zellkultur:
Benötigte Zeit in h
0
2
4
6
8
Anzahl der Zellteilungen
0
2
8
18
32
Das Wachstum der Zellkultur kann durch eine quadratische Funktion beschrieben werden.
1. Berechne die Funktionsgleichung und zeichne den Graphen in ein geeignetes Koordinatensystem.
2. Nach welcher Zeit haben 200 Zellteilungen stattgefunden?
  h
3. Wie lange dauert es, bis 1800 Teilungen erfolgt sind?
  h
5
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Der Kraftstoffverbrauch eines PKW hängt bekanntlich von der Geschwindigkeit ab. Durch Messungen wurde der funktionale Zusammenhang ermittelt. Es gilt: $\mathrm{K}\left(\mathrm{v}\right)=0{,}002\mathrm{v}^2-0{,}18\mathrm{v}+8{,}55$ für $v > 40$ .
Dabei bedeutet $K(v)$ der Kraftstoffverbrauch in $Liter/100\ km$ und $v$ die Geschwindigkeit in $km/h$ .
1. Bei welcher Geschwindigkeit beträgt der Verbrauch genau $7\frac{Liter}{100km}$ auf?
  km/h
2. Bei welcher Geschwindigkeit ist der Kraftstoffverbrauch am geringsten?
  km/h

Benötigte Zeit in h	0	2	4	6	8
Anzahl der Zellteilungen	0	2	8	18	32

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?