Betrachtet wird das bei C rechtwinklige Dreieck ABC mit den Seiten a, b und c. Ein dazu kongruentes Dreieck A'B'C' ist so positioniert, dass die Punkte C, A (bzw. B') und C' auf einer Geraden liegen und die Punkte C', A', B und C die Eckpunkte eines Trapezes bilden (vgl. Abbildung).
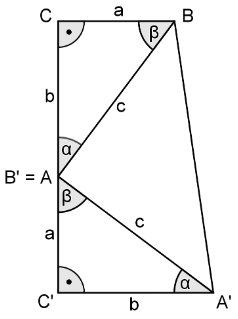
Begründen Sie, dass der Winkel ein rechter Winkel ist.
Der Flächeninhalt des Trapezes C'A'BC kann sowohl mit dem Term berechnet werden, der sich unmittelbar aus der bekannten „Trapezformel“ ergibt, als auch mit einem Term, der sich aus der Betrachtung der Teildreiecke des Trapezes ergibt. Übersetzen Sie diese Informationen in eine Gleichung und folgern Sie hieraus sie Beziehung .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
