Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Gruppe A

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

  1. 1

    Vereinfache die folgenden Terme so weit wie möglich.

    1. a8a−8=\displaystyle\frac{a^8}{a^{-8}}=

      (Verwende ^ für Potenzen)

    2. (a8)−8={(a⁸)}^{-8}=

      (Verwende ^ für Potenzen)
  2. 2
    Bodenfläche Bayerns

    Die Bodenfläche Bayerns beträgt insgesamt etwas 70 000 km². Das Diagramm zeigt wie diese genutztwird (Stand: 31.12.2015).

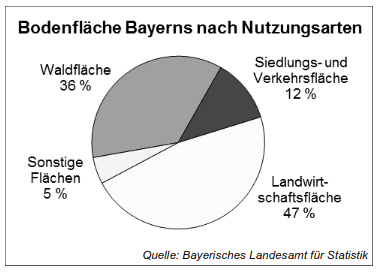
    1. Wie viele km2\text{km}^2 der Bodenfläche Bayerns sind weder Wald- noch Landwirtschaftsfläche.

    2. 40% der „Siedlungs- und Verkehrsfläche“ sind der Verkehrsfläche zuzuordnen. Geben Sie an, wie viel Prozent der Bodenfläche Bayerns demnach Verkehrsfläche sind.

    3. In Bayern wird täglich Bodenfläche in einer Größe von etwa zehn Fußballfeldern in „Siedlungs- und Verkehrsfläche“ umgewandelt. Berechnen Sie, wie viel Prozent der Bodenfläche Bayerns demnach in einem Jahr in „Siedlungs- und Verkehrsfläche“ umgewandelt werden. Gehen Sie davon aus, dass ein Fußballfeld etwa zehntausend Quadratmeter groß ist

  3. 3
    Dreieck 4

    Betrachtet wird das nebenstehende Dreieck ABC.

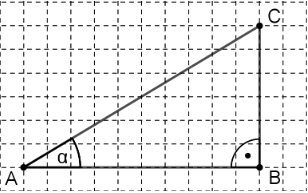
    1. Bestimmen Sie mithilfe der Abbildung den Wert von tan⁡(α)\tan\left(\alpha\right).

    2. Begründen Sie mithilfe einer geeigneten Erweiterung der Abbildung, dass die Beziehung

      tan⁡(2α)=2⋅tan⁡(α)\tan\left(2\alpha\right)=2\cdot\tan\left(\alpha\right) im Allgemeinen nicht gilt.

  4. 4

    Beim Spiel „Mäxchen“ werden zwei Laplace-Würfel geworfen. Die beiden geworfenen Augenzahlen werden als Ziffern einer zweistelligen Zahl so angeordnet, dass diese möglichst groß ist. Für die Ergebnisse ist die folgende Rangfolge festgelegt (aufsteigend geordnet):

    Mäxchen

    1. Begründen Sie: Die Wahrscheinlichkeit dafür, die Zahl 22 zu erhalten, beträgt 136\frac1{36}, und die Wahrscheinlichkeit dafür, ein Mäxchen zu erhalten, ist doppelt so groß.

    2. Lena hat die Zahl 54 erwürfelt und behauptet: „Wenn ich jetzt die beiden Würfel noch einmal werfe, beträgt die Wahrscheinlichkeit dafür, ein besseres Ergebnis zu erhalten, genau 50%“. Begründen Sie, dass Lena recht hat.

  5. 5

    Alina möchte untersuchen, ob der Regenbogen auf ihrem Foto parabelförmig ist. Dazu hat sie in das Foto ein Koordinatensystem eingezeichnet, dessen x-Achse im Ursprung den höchsten Punkt des Regenbogens berührt.

    Regenbogen

    Sie möchte die Gleichung einer Parabel aufstellen, deren Scheitel im Ursprung liegt und die durch einen weiteren Punkt P verläuft, der auf dem Regenbogen liegt. Dazu verwendet sie einen der folgenden Ansätze, wobei r > 0 gilt.

    (1) y=−(x−r)2y=-{(x-r)}^2

    (2) y=−x2+ry=-x^2+r

    (3) y=−rx2y=-rx^2

    1. Begründen Sie, dass weder Ansatz (1) noch Ansatz (2) geeignet ist

    2. Wählen Sie in der Abbildung einen geeigneten Punkt P aus und bestimmen Sie damit den Wert von rr in Ansatz (3).

    3. Beschreiben Sie, wie Alina untersuchen kann, ob die Form des Regenbogens durch die in Aufgabe b ermittelte Gleichung beschrieben werden kann.

  6. 6

    Welche der folgenden Zahlen sind rational?

  7. 7
    Dreieck

    Betrachtet wird das bei C rechtwinklige Dreieck ABC mit den Seiten a, b und c. Ein dazu kongruentes Dreieck A'B'C' ist so positioniert, dass die Punkte C, A (bzw. B') und C' auf einer Geraden liegen und die Punkte C', A', B und C die Eckpunkte eines Trapezes bilden (vgl. Abbildung).

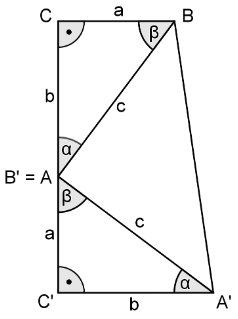
    1. Begründen Sie, dass der Winkel ∠A′AB\angle A'AB ein rechter Winkel ist.

    2. Der Flächeninhalt des Trapezes C'A'BC kann sowohl mit dem Term 12⋅(a+b)⋅(a+b)\frac12\cdot(a+b)\cdot(a+b) berechnet werden, der sich unmittelbar aus der bekannten „Trapezformel“ ergibt, als auch mit einem Term, der sich aus der Betrachtung der Teildreiecke des Trapezes ergibt. Übersetzen Sie diese Informationen in eine Gleichung und folgern Sie hieraus sie Beziehung a2+b2=c2a^2+b^2=c^2.


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?