Aufgaben zur Kraft - lernen mit Serlo!

…

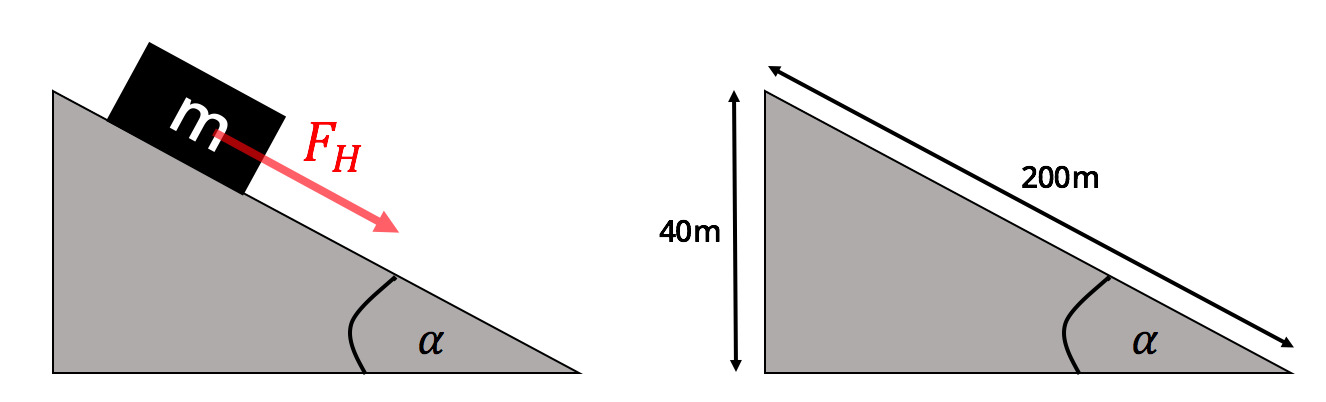
Eine Schachtel der Masse $m = 5 kg$ rutscht reibungsfrei eine schiefe Ebene runter (siehe Skizze für genauere Angaben).

Wie stark wird die Schachtel durch die Hangabtriebskraft beschleunigt?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Hangabtriebskraft

Formel der Hangabtriebskraft

Zunächst kannst du für die Hangabtriebskraft $F_{H}$ die Formel

F_{H} = m \cdot g \cdot \sin (α)

verwenden.

Sinus bestimmen

Da aber in der Angabe kein Neigungswinkel $α$ gegeben ist, musst du diesen noch bestimmen. Das kannst du mit Hilfe der Trigonometrischen Beziehung des Sinus am rechtwinkligen Dreieck.

In diesem Fall ist die Gegenkathete $40$ Meter lang und die Hypotenuse $200$ Meter.

\sin (α) = \frac{G e g e n k a t h e t e}{H y p o t e n u s e} = \frac{40 m}{200 m}

Werte einsetzen

Die gegebenen Werte kannst du jetzt einsetzen bzw. $\sin (α)$ mit $\frac{40 m}{200 m}$ ersetzen:

F_{H} = m \cdot g \cdot \sin (α) = 5 kg \cdot 9,81 \frac{m}{s^{2}} \cdot \frac{40 m}{200 m} = 9,81 N

Beschleunigung bestimmen

Die Beschleunigung bestimmst du, indem du das Aktionsprinzip (2. Newton'sche Axiom: $F = m \cdot a$ ) verwendest und mit der Hangabtriebskraft gleichsetzt. Denn dieses Axiom besagt ja, wie stark ein Körper beschleunigt wird, wenn eine Kraft auf ihn wirkt:

F_{H} \overset{!}{=} m \cdot a | : m

\Leftrightarrow \frac{F_{H}}{m} = a

Also

a = \frac{9,81 N}{5 kg} = \frac{9,81 \frac{kg \cdot m}{s^{2}}}{5 kg} \approx 1,96 \frac{m}{s^{2}}

Die Schachtel wird also durch die Hangabtriebskraft mit $1,96 \frac{m}{s^{2}}$ beschleunigt.

Du benötigst die Formel für Hangabtriebskraft
Als nächstes musst du den Sinus bestimmen
Setze nun die Werte ein
Dann bestimmst du die Beschleunigung

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0

serlo.org CC BY-SA 4.0

→ Was bedeutet das?