Berechne den Flächeninhalt des rechts abgebildeten Baums.
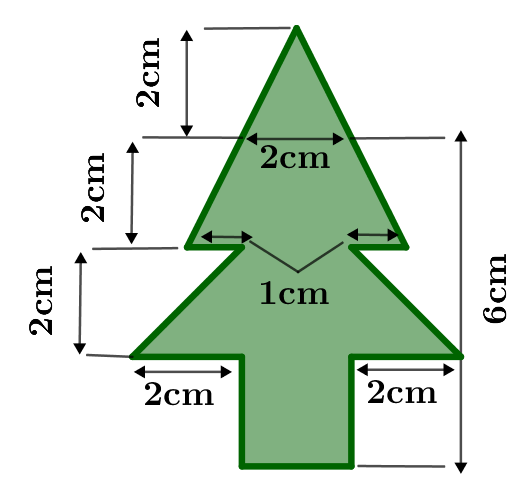
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt zusammengesetzter Figuren
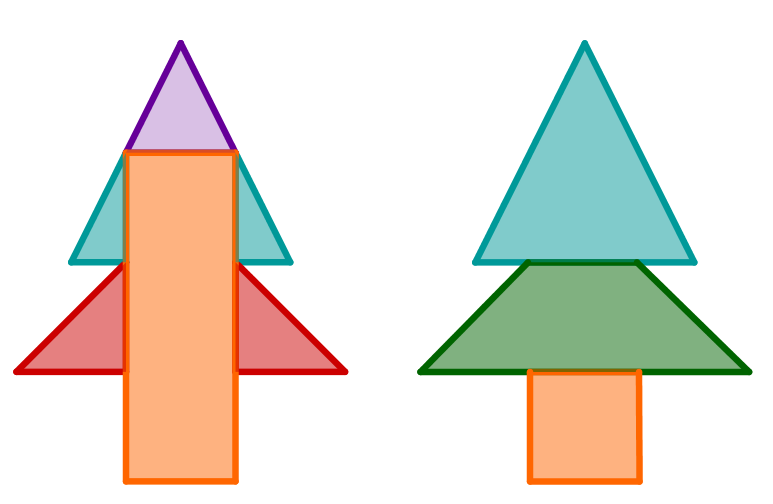
Die Berechnung über eine Zerlegung in Drei- und Rechtecke ist hier näher ausgeführt.
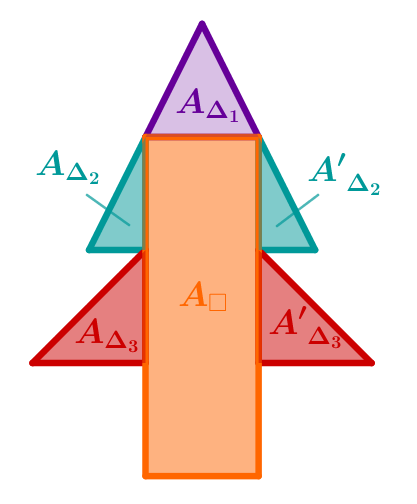
Der Flächeninhalt ergibt sich dann aus der Summe der Flächeninhalte der Drei- und Rechtecke der Zerlegung, also:
Da der Baum symmetrisch ist, gelten folgende Beziehungen:
Also gilt :
Nun kannst du die Flächeninhalte der Dreiecke und des Rechtecks berechnen.
Flächeninhalt der Dreiecke
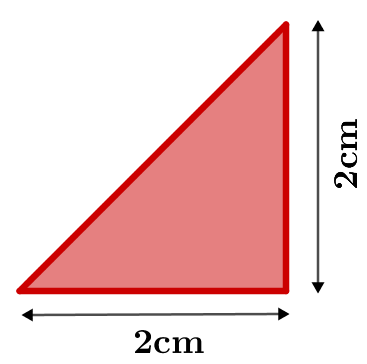
Zur Bestimmung des Flächeninhalts der Dreiecke und benötigst du die Flächeninhaltsformel für rechtwinklige Dreiecke.
Flächeninhalt :
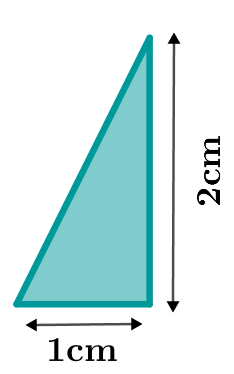
Flächeninhalt :
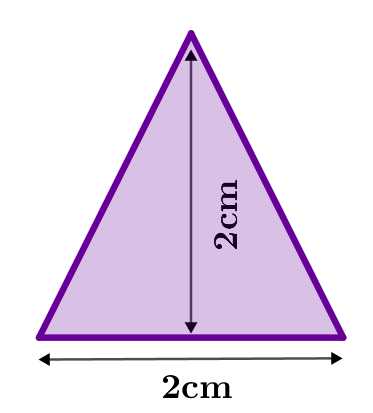
Zur Bestimmung des Flächeninhalts der Dreiecke benötigst du die Flächeninhaltsformel für Dreiecke.
Flächeninhalt :
Flächeninhalt der Rechtecke
Zur Bestimmung des Flächeninhalts des Rechtecks brauchst du die Flächeninhaltsformel für Rechtecke.
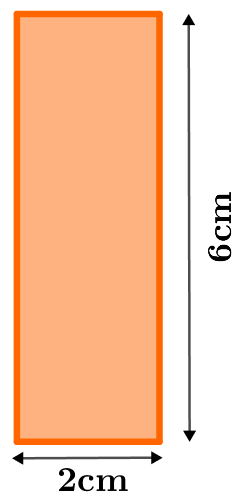
Berechnung des Flächeninhalts des Baums
Nun kannst du die Flächeninhalte der Dreiecke und des Rechtecks addieren, um zu bestimmen.
Der Flächeninhalt des Baums beträgt somit .
Versuche den Baum in Formen zu zerlegen, deren Flächeninhalt du leicht berechnen kannst.
Es gibt viele verschiedene Möglichkeiten, um diese Aufgabe zu lösen.
Die vermutlich üblichste Möglichkeit ist es, den Baum in Figuren zu zerlegen, deren Flächeninhalt du leichter berechnen kannst.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
