Dieser Artikel listet alle Formeln auf, die zur Berechnung der Fläche von ebenen Figuren wichtig sind. Verschiedenen Formen von Dreiecken und Vierecken sowie die Flächenberechnung eines Kreises werden vorgestellt.
Dreiecke
Der Buchstabe A steht hier jeweils für den Flächeninhalt des zugehörigen Dreiecks.
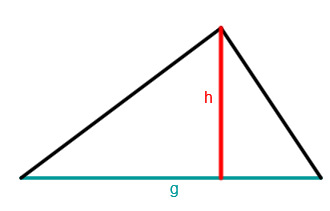
Allgemeines Dreieck
Für jedes ebene Dreieck kann folgende Flächenformel verwendet werden:
Dabei darf man eine beliebige Seite als Grundseite g und die darauf stehende Höhe h verwenden.
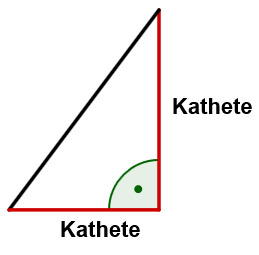
Rechtwinkliges Dreieck
Bei rechtwinkligen Dreiecken muss man zur Berechnung der Fläche nicht extra die Länge einer Höhe berechnen. Es reicht die Länge der beiden Katheten.
Vierecke
Auch hier steht A für den Flächeninhalt des zugehörigen Vierecks.
Allgemein kann man die Fläche eines Vierecks berechnen, indem man es in zwei Dreiecke zerlegt.
Danach ergibt sich

Bei den folgenden speziellen Vierecken kommt man aber mit der jeweiligen Formel schneller zum Ergebnis.
Rechteck
Bei einem Rechteck benötigt man die Länge und die Breite, um die Fläche zu berechnen.

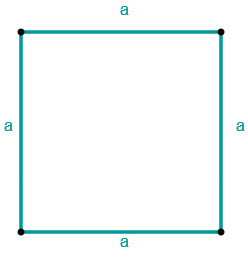
Quadrat
Da bei einem Quadrat alle Seiten gleich lang sind, benötigt man zur Berechnung der Fläche nur die Länge einer Seite.
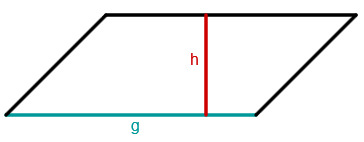
Parallelogramm
Zur Berechnung der Fläche eines Parallelogramms benötigt man die Länge einer Seite und der dazugehörigen Höhe.
Hierbei kann man eine beliebige Seite und die dazugehörige Höhe wählen.
Drachenviereck
Die Fläche eines Drachenvierecks ist die Hälfte des Produkts seiner Diagonalen.
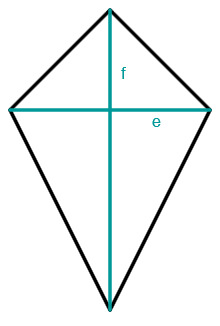
Raute
Genau wie beim Drachenviereck berechnet sich die Fläche einer Raute mithilfe der beiden Diagonalen.

Trapez
Zur Berechnung der Fläche eines Trapezes benötigt man die Länge der parallelen Seiten und der Höhe.
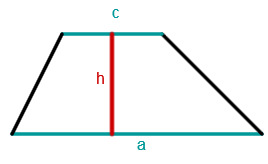
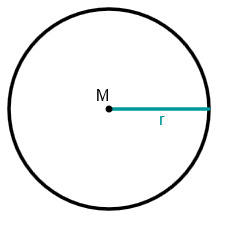
Kreis
Um die Fläche eines Kreises zu berechnen, benötigt man den Radius r und die Kreiszahl .
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
