Ein Ortsvektor ist der Vektor vom Ursprung zu einem bestimmten Punkt. Er hat die gleichen Koordinaten wie der Punkt selbst. Der Ortsvektor zum Punkt ist zum Beispiel . Man schreibt auch statt verkürzt . Üblich ist auch, den entsprechenden Kleinbuchstaben zu verwenden, also zum Beispiel für oder für . Möchte man den Gegenvektor, also den vom Punkt zum Ursprung haben, muss man nur die Vorzeichen des Vektors umdrehen, also statt mit rechnen.
Mithilfe von Ortsvektoren und Vektorketten können Koordinaten im Raum berechnet werden.
Beispiel
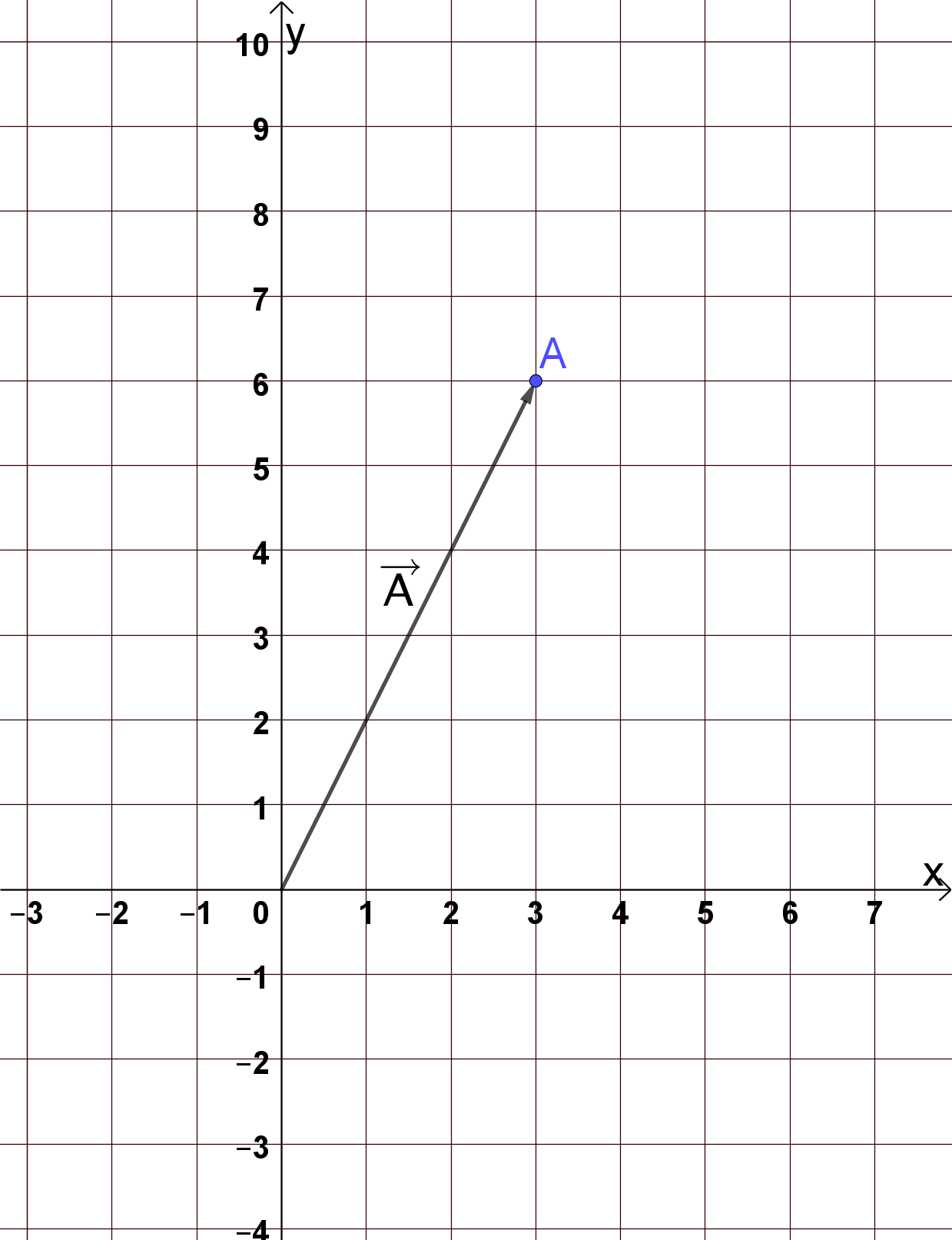
Im Koordinatensystem ist der Punkt eingezeichnet. Der zugehörige Ortsvektor verbindet den Ursprung mit dem Punkt A und wird durch ausgedrückt.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
