Mithilfe von Addition, Subtraktion und skalarer Multiplikation kann man mehrere Vektoren aneinander hängen. Diese Verbindung mehrerer Vektoren nennt man Vektorkette.
Bei einer Vektorkette wird stets der Fuß des vorherigen Vektors an die Spitze des nächsten Vektors gehängt.
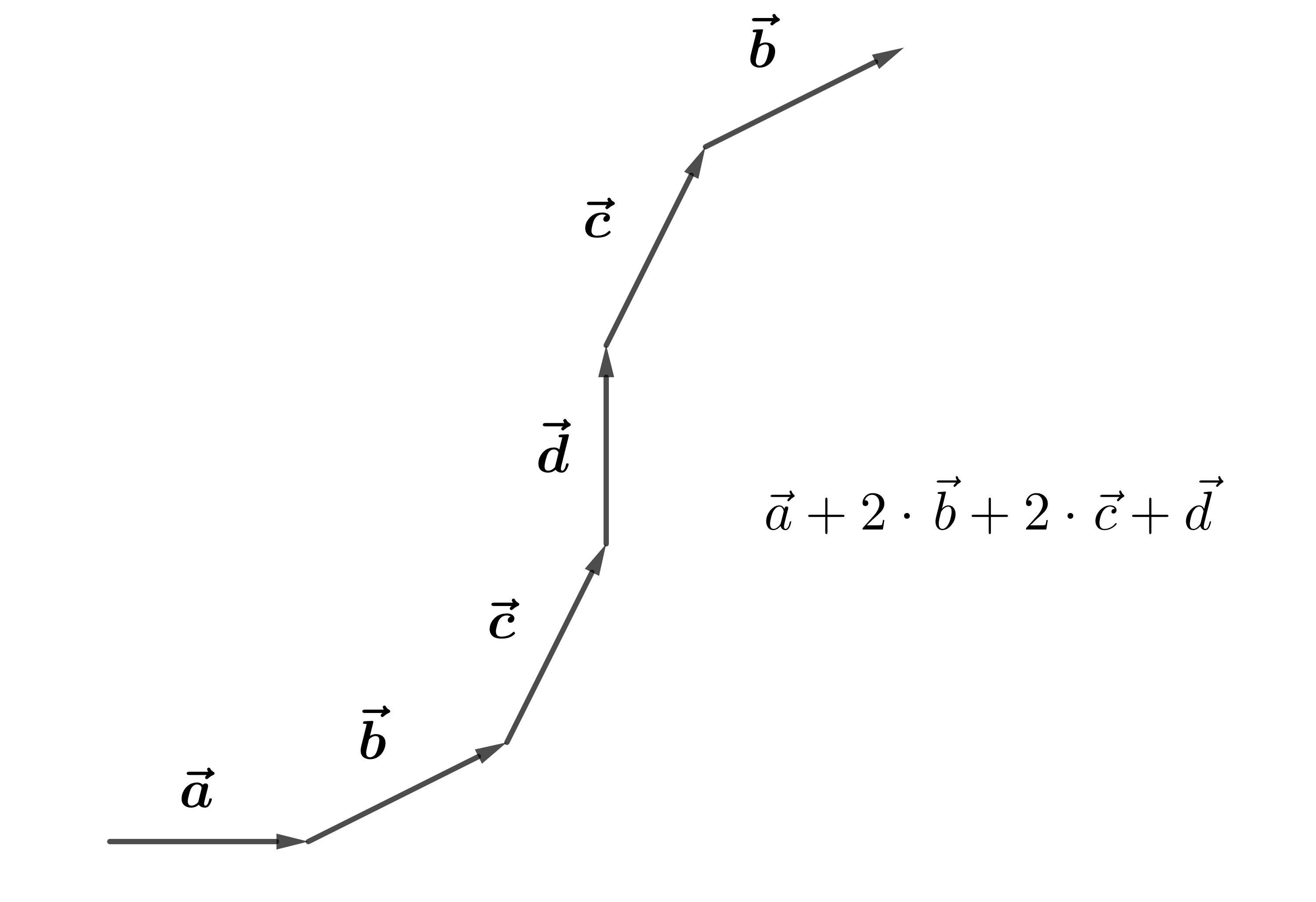
Beispiel einer Vektorkette
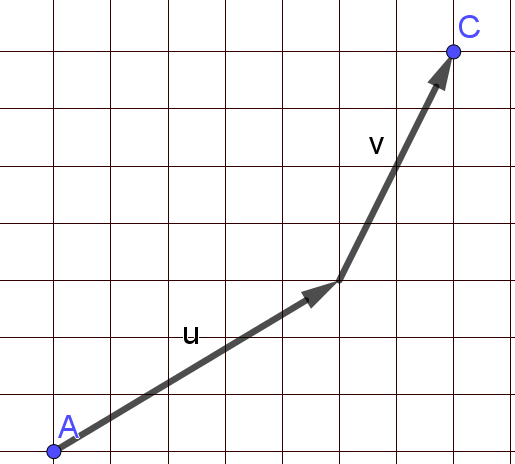
Um von Position A zu Position C zu gelangen, muss man die Summe aus den Vektoren und bilden:
Vektorkette:
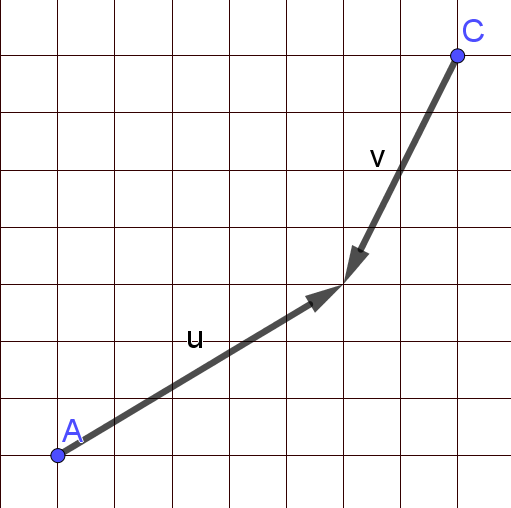
Um von Position A zu Position C zu kommen, muss man den Vektor zunächst umkehren, denn die Vektoren müssen immer "mit Fuß an Spitze" verbunden werden:
Vektorkette:
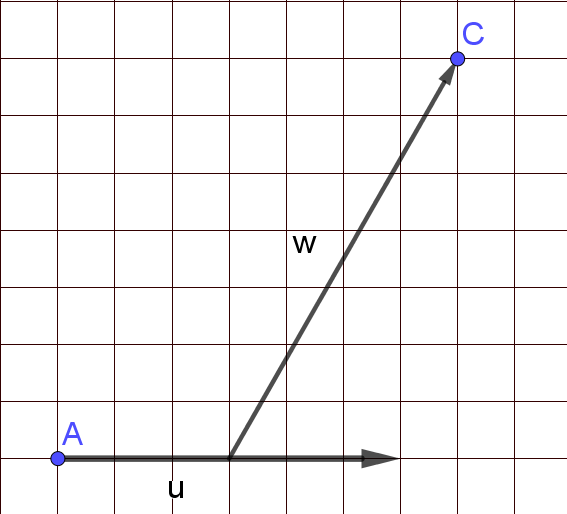
Um zur Position C zu gelangen, muss der Vektor nur zur Hälfte durchlaufen werden (3 Kästchen von insgesamt 6):
Vektorkette:
Vektorketten im Koordinatensystem
Da Vektoren ortsunabhängig sind, also man aufgrund der Koordinaten nicht entscheiden kann, wo der Repräsentant des Vektors liegt, kann man mit Vektoren allein keine Koordinaten bestimmen. Beginnst du allerdings mit einem Ortsvektor, kannst du Koordinaten mithilfe von Vektorketten ausdrücken:
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
