Geometrie, Teil B, Aufgabengruppe 1

Die Abbildung 1 zeigt modellhaft eine Mehrzweckhalle, die auf einer horizontalen Fläche steht und die Form eines geraden Prismas hat.

Die Punkte $A_{1} (0 ∣ 0 ∣ 0)$ , $A_{2} (20 ∣ 0 ∣ 0)$ , $A_{3}$ und $A_{4} (0 ∣ 10 ∣ 0)$ stellen im Modell die Eckpunkte der Grundfläche der Mehrzweckhalle dar, die Punkte $B_{1}$ , $B_{2}$ , $B_{3}$ und $B_{4}$ die Eckpunkte der Dachfläche. Diejenige Seitenwand, die im Modell in der $x_{1} x_{3} -$ Ebene liegt, ist $6 \ \text{m}$ hoch, die ihr gegenüberliegende Wand nur $4\ \text{m}$ .

Eine Längeneinheit im Koordinatensystem entspricht $1\ \text{m}$ , d.h. die Mehrzweckhalle ist $20\ \text{m}$ lang.

a) Geben Sie die Koordinaten der Punkte $B_{2}$ , $B_{3}$ und $B_{4}$ an und bestätigen Sie, dass diese Punkte in der Ebene $E : x_{2} + 5 x_{3} - 30 = 0$ liegen.

b) Berechnen Sie die Größe des Neigungswinkels der Dachfläche gegenüber der Horizontalen.

c) Der Punkt $T (7 ∣ 10 ∣ 0)$ liegt auf der Kante $\left[A_3A_4 \right]$ . Untersuchen Sie rechnerisch, ob es Punkte auf der Kante $\left[B_3B_4 \right]$ gibt, für die gilt: Die Verbindungs-strecken des Punktes zu den Punkten $B_{1}$ und $T$ stehen aufeinander senkrecht. Geben Sie gegebenenfalls die Koordinaten dieser Punkte an.

Der Punkt $L$ , der vertikal über dem Mittelpunkt der Kante $\left[A_1A_2\right]$ liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die $12\ \text{m}$ über der Grundfläche angebracht ist. Die als punktförmig angenommene Lichtquelle beleuchtet – mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände – das gesamte Gelände um die Halle.

d) Die Punkte $L$ , $B_{2}$ und $B_{3}$ legen eine Ebene $F$ fest. Ermitteln Sie eine Gleichung von $F$ in Normalenform.

(zur Kontrolle : $F : 3 x_{1} + x_{2} + 5 x_{3} - 90 = 0$ )

e) Die Ebene $F$ schneidet die $x_{1} x_{2}$ -Ebene in der Gerade $g$ . Bestimmen Sie eine Gleichung von $g$ .

(zur Kontrolle: $g:\vec{X} = \begin{pmatrix} 30\\0\\0 \end{pmatrix}+ \lambda \cdot \begin{pmatrix} 1 \\ -3\\ 0 \end{pmatrix} , \lambda \in \R$ )

f) Die Abbildung 2 zeigt den Grundriss des Hallenmodells in der $x_{1} x_{2}$ -Ebene. Stellen Sie unter Verwendung der bisherigen Ergebnisse den Schattenbereich der Flutlichtanlage in der Abbildung exakt dar.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus drei Punkten erstellen

Teilaufgabe a)

Gegeben sind die Punkte $A_{1} (0 ∣ 0 ∣ 0)$ , $A_{2} (20 ∣ 0 ∣ 0)$ , $A_{3}$ und $A_{4} (0 ∣ 10 ∣ 0)$ .

Diejenige Seitenwand, die im Modell in der $x_{1}$ - $x_{3}$ -Ebene liegt, ist 6 m hoch, die ihr gegenüberliegende Wand nur 4 m.

Die Punkte $B_1;\ B_2;\ B_3;\ B_4$ haben also die Koordinaten:

$B_1\left(0|0|6\right)$ ; $B_2\left(20|0|6\right);B_3\left(20|10|4\right);B_4\left(0|10|4\right)$

Die einfachste Möglichkeit ist es, einfach nachzurechnen, dass diese Punkte die Ebenengleichung $x_{2} + 5 x_{3} - 30 = 0$ erfüllen:

$5\cdot 6-30=0\quad \checkmark$ ( $B_{1}$ und $B_{2}$ )

$10+5\cdot4-30=0\quad \checkmark$ ( $B_{3}$ und $B_{4}$ ).

Man kann natürlich $E$ auch berechnen:

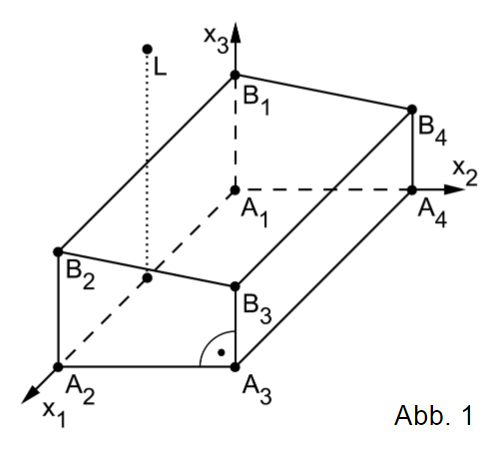
Die Ebene E in Parameterform lautet

$\def\arraystretch{1.25} E:\vec{x}=\left(\begin{array}{c}20\\0\\6 \end{array}\right)+\lambda\left(\begin{array}{c}0\\10\\-2 \end{array}\right)+\rho\left(\begin{array}{c}-20\\10\\-2 \end{array}\right)$

$\def\arraystretch{1.25} \vec{u}=\left(\begin{array}{c}0\\10\\-2 \end{array}\right);\vec{v}=\left(\begin{array}{c}-20\\10\\-2 \end{array}\right)$

Um den Normalenvektor zu bestimmen, bilden wir das Vektorprodukt von $\vec{u}$ und $\vec{v}$ :

$\def\arraystretch{1.25} \vec{u}\times \vec{v}=\left(\begin{array}{c}0\\10\\-2 \end{array}\right)\times\left(\begin{array}{c}-20\\10\\-2 \end{array}\right)=\begin{pmatrix}0\\4\\20 \end{pmatrix}$ . Da es nur auf die Richtung ankommt, kürzen wir durch 4 und nehmen $\def\arraystretch{1.25} \vec{n}=\left(\begin{array}{c} 0\\1\\5 \end{array}\right)$ .

Weil die zweiten und dritten Komponenten von $\vec{u}$ und $\vec{v}$ gleich sind, gibt es hier noch einen anderen Weg:

Man schreibt als Normalenvektor $\def\arraystretch{1.25} \vec{n}=\left(\begin{array}{c}t\\2\\10\end{array}\right)$ ;

wobei der Wert der ersten Komponente vorerst beliebig bleibt.

Jedenfalls gilt immer: Das Skalarprodukt $\vec{u}\circ\vec{n}=0$ .

Nun bildet man das Skalarprodukt $\vec{v}\circ\vec{n}=-20t+20-20\Rightarrow t=0$ .

Damit gilt: $\def\arraystretch{1.25} \vec{n}=\left(\begin{array}{c} 0\\2\\10 \end{array}\right)$ .

Oder gekürzt: $\def\arraystretch{1.25} \vec{n}=\left(\begin{array}{c} 0\\1\\5 \end{array}\right)$ .

Auf diese Weise spart man sich die Berechnung des Vektorproduktes und vermeidet dadurch unnötige Rechenfehler.

Nun bildet man das Skalarprodukt aus dem berechneten Normalenvektor $\vec{n}$ mit dem Ortsvektor $\vec{x}$ der Ebene in Parameterform und erhält

$\def\arraystretch{1.25} \left(\begin{array}{c}0\\1\\5 \end{array}\right)\circ\vec{x}=\left(\begin{array}{c}0\\1\\5 \end{array}\right)\circ\left(\begin{array}{c}20\\0\\6 \end{array}\right)=30\iff x_2+5x_3-30=0$

Teilaufgabe b)

Berechnung des Winkels zwischen der Dachfläche und der Horizontalen ist der Winkel zwischen der Ebene E und der $x_{1}$ - $x_{2}$ -Ebene.

Der Winkel zwischen zwei Ebenen entspricht dem Winkel zwischen den jeweiligen Normalenvektoren.

Der Normalenvektor $\def\arraystretch{1.25} \vec{n}=\left(\begin{array}{c} 0\\1\\5 \end{array}\right)$ der Ebene $E$ hat die Länge $\sqrt{1^2+5^2}=\sqrt{26}$

Ein Normalenvektor der $x_{1}$ - $x_{2}$ -Ebene ist $\def\arraystretch{1.25} \left(\begin{array}{c}0\\0\\1 \end{array}\right)$ und hat die Länge $\sqrt{1}=1$ .

Damit gilt für $\cos(\alpha)=\dfrac{5}{\sqrt{26}}\Rightarrow \alpha=11{,}3°$

wobei $5$ der Wert des Skalarproduktes von $\def\arraystretch{1.25} \left(\begin{array}{c} 0\\1\\5 \end{array}\right)\circ\left(\begin{array}{c} 0\\0\\1 \end{array}\right)=5$ .

Oder $\tan(\alpha)=\frac{1}{5}\Rightarrow \alpha=11{,}3°$

Teilaufgabe c)

Berechne einen Punkt $S$ auf der Kante $[B_{3} B_{4}]$ , sodass die Verbindungsstrecken des Punktes $S$ zu $B_{1}$ und $T(7\left|10\left|0)\right|\right|$ senkrecht aufeinander stehen.

Die $x$ -Koordinate des Punktes $S$ ist unbekannt und wird mit $s$ bezeichnet.

Damit hat $S$ die Koordinaten $S(s\left|10\right|4)$ . $B_1\left(0\left|0\right|6\right)$

$\overrightarrow{SB}=\vec{v}=\begin{pmatrix}-s\\-10\\2 \end{pmatrix}; \overrightarrow{ST}=\vec{u}=\begin{pmatrix}7-s\\0\\-4 \end{pmatrix}$

Die Vektoren $\vec{v}$ und $\vec{u}$ sind orthogonal, wenn das Skalarprodukt gleich null ist.

$\begin{pmatrix}-s\\-10\\2 \end{pmatrix}\circ\begin{pmatrix}7-s\\0\\-4 \end{pmatrix}=-s(7-s)-8=0\iff s^2-7s-8=0$

Lösung über quadratische Ergänzung:

$s^2-7s+(\dfrac{7}{2})^2=8+\dfrac{49}{4}\iff (s-\dfrac{7}{2})^2=\dfrac{32+49}{4}\iff$

$(s-\dfrac{7}{2})^2=\dfrac{81}{4}\iff s-\dfrac{7}{2}=\dfrac{9}{2} \text{\ oder\ } s-\dfrac{7}{2}=-\dfrac{9}{2}\iff$

$s=\dfrac{7+9}{2}\text{\ oder\ } s=\dfrac{7-9}{2}\iff s=8\text{ \ oder\ } s=-1$

Damit gibt es einen Punkt $S (8 ∣ 10 ∣ 4)$ mit der geforderten Eigenschaft.

Der Punkt $R (- 1 ∣ 10 ∣ 4)$ liegt außerhalb der Kante $\left[B_3B_4\right]$

Teilaufgabe d)

Die Spitze der Lampe $L$ hat die Koordinaten $L\left(10\left|0\right|12\right)$

Ermittele eine Gleichung der Ebene $F$ durch die Punkte $L, B_{2}$ und $B_{3}$

$F:\vec{x}=\begin{pmatrix}10\\0\\12 \end{pmatrix}+\lambda\begin{pmatrix}10\\0\\-6 \end{pmatrix}+\mu\begin{pmatrix}10\\10\\-8 \end{pmatrix}$ .

Der Normalenvektor $\vec{n}$ wird mit dem Vektorprodukt der Richtungsvektoren bestimmt:

$\begin{pmatrix}10\\0\\-6 \end{pmatrix}\times\begin{pmatrix}10\\10\\-8 \end{pmatrix}=\begin{pmatrix}60\\20\\100 \end{pmatrix}$ . Wieder kommt es auf die Länge nicht an und wir wählen $\vec{n}=\begin{pmatrix}3\\1\\5\end{pmatrix}$ .

Und als Ebenengleichung in Punkt-Normalenform:

$F:\begin{pmatrix}3\\1\\5 \end{pmatrix}\circ\vec{x}=\begin{pmatrix}3\\1\\5\end{pmatrix}\circ\begin{pmatrix}10\\0\\12\end{pmatrix}\iff3x_1+x_2+5x_3-90=0$ .

Teilaufgabe e)

Für die Gleichung der $x_{1}$ - $x_{2}$ -Ebene kann man die Punkt-Richtungsform oder eine Normalenform verwenden.

$E_{x_1x_2}:\vec{x}=\lambda\begin{pmatrix}1\\0\\0\end{pmatrix}+\mu\begin{pmatrix}0\\1\\0\end{pmatrix}$

man setzt $E_{x_1x_2}$ in die Ebene $F$ ein:

$\begin{pmatrix}3\\1\\5\end{pmatrix}[\lambda\begin{pmatrix}1\\0\\0\end{pmatrix}+\mu\begin{pmatrix}0\\1\\0\end{pmatrix}]-90=0\iff3\lambda+\mu=90\iff \mu=90-3\lambda$

Das setzen wir in $E_{x_1x_2}$ ein:

$\vec{x}=\lambda\begin{pmatrix}1\\0\\0\end{pmatrix}+90\begin{pmatrix}0\\1\\0\end{pmatrix}-3\lambda\begin{pmatrix}0\\1\\0\end{pmatrix} =\begin{pmatrix}0\\90\\0\end{pmatrix}+\lambda\begin{pmatrix}1\\-3\\0\end{pmatrix}$

Um die Gleichung der Kontrolle zu erhalten, setzt man $\lambda=30$ und sieht, dass der Punkt $\begin{pmatrix}0\\90\\0\end{pmatrix}+30\begin{pmatrix}1\\-3\\0\end{pmatrix}=\begin{pmatrix}30\\0\\0 \end{pmatrix}$ in der Ebene liegt.

$g:\vec{x}=\begin{pmatrix}30\\0\\0\end{pmatrix}+\lambda'\begin{pmatrix}1\\-3\\0\end{pmatrix}$

Teilaufgabe f)

Man betrachtet vier Lichtstrahlen von $L$ aus. Die $x_{1}$ - $x_{2}$ -Ebene hat die Normalenform

$\vec{x}\circ\begin{pmatrix}0\\0\\1 \end{pmatrix}=0$

$l_1:[LB_2] :\vec{x}=\begin{pmatrix}10\\0\\12\end{pmatrix}+\lambda\begin{pmatrix}10\\0\\-6\end{pmatrix}$

$l_1\text{\ in\ } E_{x_1x_2}:\begin{pmatrix}0\\0\\1\end{pmatrix}\left[\begin{pmatrix}10\\0\\12\end{pmatrix}+\lambda\begin{pmatrix}10\\0\\-6\end{pmatrix}\right]=0\iff12-6\lambda=0$

$\lambda=2\text{\ in\ } l_1:S_1(30|0|0)$ Schattenpunkt

$l_2:[LB_3]:\vec{x}=\begin{pmatrix}10\\0\\12\end{pmatrix}+\mu\begin{pmatrix}10\\10\\-8\end{pmatrix}\text{\ in\ } E_{x_1x_2}$

$\begin{pmatrix}0\\0\\1\end{pmatrix}\left[\begin{pmatrix}10\\0\\12\end{pmatrix}+\mu\begin{pmatrix}10\\10\\-8\end{pmatrix}\right]=0\iff12-8\mu=0\iff\mu=\frac{3}{2}$

in $l_{2} : S_{2} (25 ∣ 15 ∣ 0)$ Schattenpunkt

Durch die Punkte $S_{1}$ und $S_{2}$ wird die Schattenlinie $S L_{1}$ beschrieben.

Aus Symmetriegründen ergeben sich für die Schattenpunkte $S_3\text\ und S_4$ aus den Lichtstrahlen $l_{3} : [L B_{1}]$ und $l_{4} : [L B_{4}]$ : $S_{3} (- 10 ∣ 0 ∣ 0)$ und $S_{4} (- 5 ∣ 15 ∣ 0)$ .

Innerhalb des Trapezes HEFG ohne das Dach ABCD ist Schatten

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?