Geometrie, Teil B, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
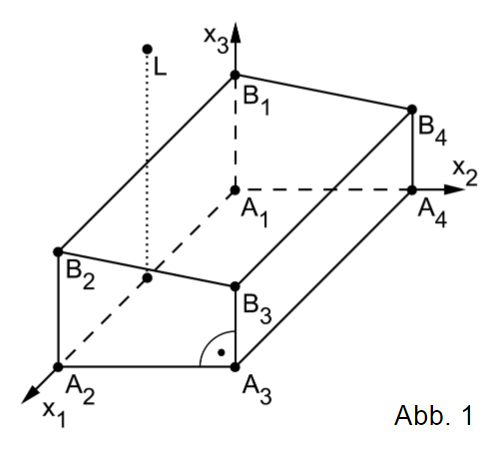
Die Abbildung 1 zeigt modellhaft eine Mehrzweckhalle, die auf einer horizontalen Fläche steht und die Form eines geraden Prismas hat.
Die Punkte , , und stellen im Modell die Eckpunkte der Grundfläche der Mehrzweckhalle dar, die Punkte , , und die Eckpunkte der Dachfläche. Diejenige Seitenwand, die im Modell in der Ebene liegt, ist hoch, die ihr gegenüberliegende Wand nur .
Eine Längeneinheit im Koordinatensystem entspricht , d.h. die Mehrzweckhalle ist lang.
a) Geben Sie die Koordinaten der Punkte , und an und bestätigen Sie, dass diese Punkte in der Ebene liegen.
b) Berechnen Sie die Größe des Neigungswinkels der Dachfläche gegenüber der Horizontalen.
c) Der Punkt liegt auf der Kante . Untersuchen Sie rechnerisch, ob es Punkte auf der Kante gibt, für die gilt: Die Verbindungs-strecken des Punktes zu den Punkten und stehen aufeinander senkrecht. Geben Sie gegebenenfalls die Koordinaten dieser Punkte an.
Der Punkt , der vertikal über dem Mittelpunkt der Kante liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die über der Grundfläche angebracht ist. Die als punktförmig angenommene Lichtquelle beleuchtet – mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände – das gesamte Gelände um die Halle.
d) Die Punkte , und legen eine Ebene fest. Ermitteln Sie eine Gleichung von in Normalenform.
(zur Kontrolle : )
e) Die Ebene schneidet die -Ebene in der Gerade . Bestimmen Sie eine Gleichung von .
(zur Kontrolle: )
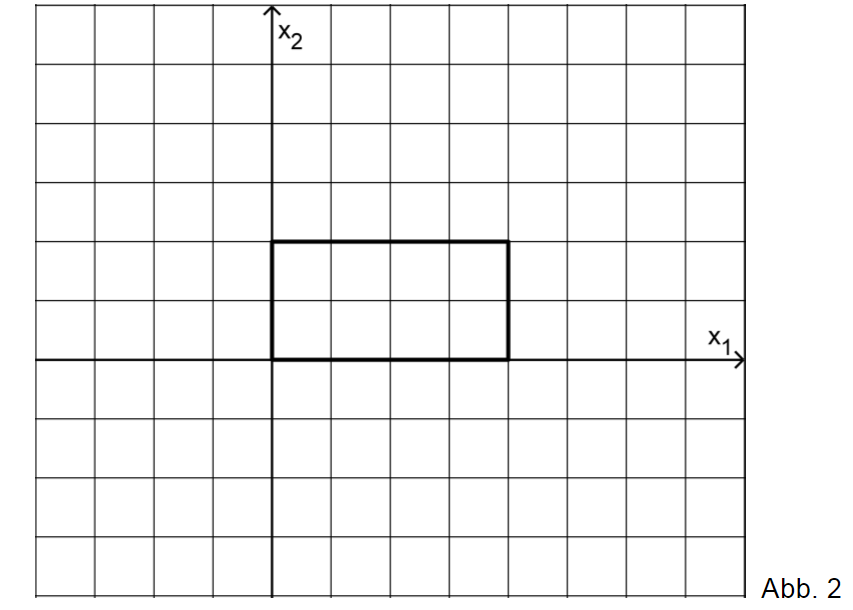
f) Die Abbildung 2 zeigt den Grundriss des Hallenmodells in der -Ebene. Stellen Sie unter Verwendung der bisherigen Ergebnisse den Schattenbereich der Flutlichtanlage in der Abbildung exakt dar.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?