Scheitelform

Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: allgemeine Form und Scheitelform einer quadratischen Funktion

Erklärung:

Die Scheitelform ist eine Formel von einer Parabel von der man den Scheitelpunkt direkt ablesen kann.

Sie lautet:     $f\left(x\right)=\left(x-d\right)^2+e$                             

Wenn man nun den Scheitelpunkt direkt ablesen will muss man nur die Zahlen richtig einsetzen.

Zum Beispiel so:    $f\left(x\right)=\left(x-7\right)^2+5$ =  Scheitelpunkt = (7/5)

(WICHTIG = WENN  d  NEGATIV IST, IST BEIM SCHEITELPUNKT  x  POSITIV) !!! Gilt auch andersrum !!!

Umwandlung in Normalform:

Beispiel:    2 (x – 3)² + 4                               

                 = 2 (x² - 6x + 9) + 4                         |  Zuerst die bionomische Formel aufgelösen.

                 = 2x² - 12x + 18 + 4                        | Danach muss man faktorisieren.

                 = 2x² - 12x + 22

Beispiel:

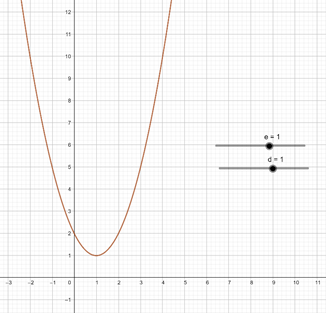
Hier sieht man als Beispiel eine Parabel, welche den Scheitelpukt (1/1) hat.

Die Formel hierfür würde nun $f\left(x\right)=\left(x-1\right)^2+1$ lauten.

Beispiel Aufgaben:

1) Umwandlung in Normalform:

a) $f\left(x\right)=\left(x-3\right)^2-4$

b) $f\left(x\right)=2\left(x+7\right)^2+1$

2) Ablesen des Scheitelpunkts:

a) $f\left(x\right)=\left(x-5\right)^2+9$

b) $f\left(x\right)=\left(x+3\right)^2-2$