Die Ergebnismenge, die man bei einem Zufallsexperiment, wie zum Beispiel einem Würfelwurf mit zwei Würfeln, betrachten kann, lässt sich auf die untersuchte Fragestellung anpassen. Dabei lässt sich diese beispielsweise vergröbern oder verfeinern.
Wenn man zu einem Zufallsexperiment einen Ergebnisraum sucht, muss man sich darüber klar werden, was alles bei diesem Experiment im Zusammenhang der Aufgabenstellung beachtet werden muss. Je nachdem kann der Ergebnisraum unterschiedlich aussehen.
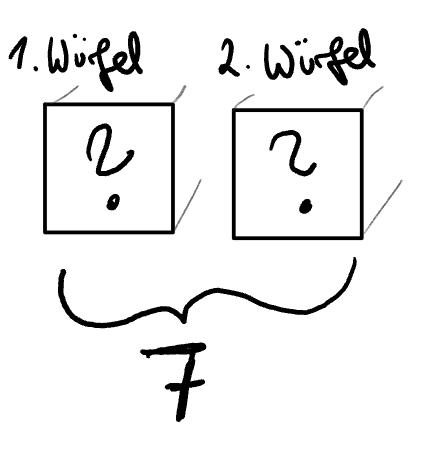
Beispiel 1: Augensumme
Soll am Ende nur betrachtet werden, welche Summe die beiden Augenzahlen bilden, so betrachtet man die Ergebnismenge .
Die einzelnen Ergebnisse sind dabei nicht gleichwahrscheinlich. Denn damit die Summe gewürfelt wird, müssen mit den Würfeln eine und eine geworfen werden, wohingegen eine mit den Kombinationen erzielt werden kann.
Beispiel 2: gerade Augensumme
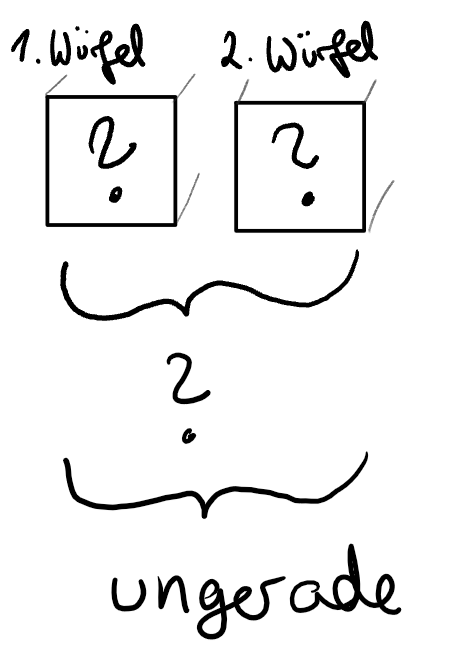
Interessiert man sich nur dafür, ob die Augensumme gerade ist, so lässt sich die obere Ergebnismenge vergröbern.
Es wird also bei der Auswertung nicht mehr aufgeschrieben, ob die Augensumme 2 oder 4 ist, sondern nur, dass sie gerade ist:
Beispiel 3: Würfelergebnis
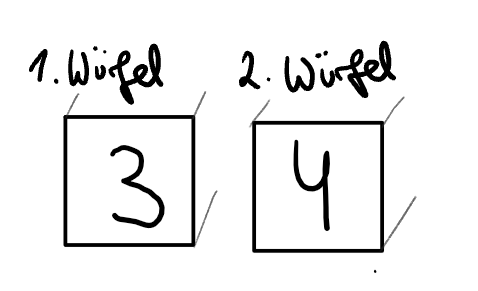
Möchte man genau erfassen, welche Zahl auf welchem Würfel zu sehen ist, so kann die Ergebnismenge verfeinert angegeben werden. Der Vorteil hierbei ist, dass es sich um ein Laplace-Experiment handelt. Alle Ereignisse sind also gleich wahrscheinlich.
Die Ergebnismenge ist jedoch sehr groß und unhandlich, da sie aus Paaren (Augenzahl 1. Würfel, Augenzahl 2. Würfel) besteht:
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
