Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Zufallsexperiment

Ein Zufallsexperiment ist ein Experiment...

  • mit zufälligem Ergebnis (Ausgang),

  • mit mindestens zwei verschiedenen Ergebnissen,

  • welches reproduzierbar (wiederholbar) ist.

Bild 1: Würfelwurf

Bild 1: Würfelwurf

Beispiele für Zufallsexperimente

Beispiel: Werfen eines Würfels

  • Vor dem Würfeln ist die geworfene Augenzahl noch unbekannt.

  • Es sind Augenzahlen zwischen 1 und 6 möglich.

  • Man kann den Wurf unendlich oft unter den gleichen Voraussetzungen durchführen.

Das Würfel-Experiment ist daher ein Zufallsexperiment.

Bild 2: Würfelwurf

Bild 2: Würfelwurf

Beispiel: Werfen einer Münze

  • Vor dem Wurf der Münze ist noch unbekannt auf welcher Seite sie landen wird.

  • Nach dem Wurf kann die Münze zwei verschiedene Ergebnisse haben. - (Kopf oder Zahl)

  • Man kann den Wurf der Münze beliebig oft wiederholen.

Der Münzwurf ist daher ein Zufallsexperiment.

Bild 3: Münzwurf

Bild 3: Münzwurf

Gegenbeispiel für ein Zufallsexperiment

Beispiel: Tippen auf den Ausgang eines Fußballspiels

  • Vor dem Spiel ist noch unbekannt, wer das Spiel gewinnen wird.

  • Da zwei Mannschaften gegeneinander spielen, gibt es zwei mögliche Gewinner bzw. Verlierer.

  • ABER: Dieses Spiel kann niemals unter denselben Bedingungen wiederholt werden. Bei jedem Spiel gibt es andere Bedingungen (Krankheit, Wetter, Müdigkeit).

Definition

Beispiel

Ergebnis

Jeder spezifische Ausgang eines Experiments wird als Ergebnis bezeichnet.

Beim Wurf eines Würfels ist der Ausgang "Es fällt eine 3." ein mögliches Ergebnis.

Ergebnisraum

Im Ergebnisraum sind alle möglichen Ergebnisse enthalten. Der Ergebnisraum wird häufig mit dem griechischen Buchstaben Ω\Omega ("omega") bezeichnet.

Beim Wurf eines Würfels ist der Ergebnisraum

Ω={1;2;3;4;5;6} \Omega = \{1;2;3;4;5;6\}.

Ereignis

Ein Ereignis kann aus einem oder mehreren Ergebnissen eines Zufallsexperiments bestehen.

Beim Wurf eines Würfels ist der Ausgang "es fällt eine ungerade Zahl" ein Ereignis. Es enthält die Ergebnisse "es fällt eine 1","es fällt eine 3", oder "es fällt eine 5". Dieses Ereignis kann als Zahlenmenge geschrieben werden:

"Es fällt eine ungerade Zahl" = {1;3;5}\{1;3;5\}.

Wahrscheinlichkeit

Die Wahrscheinlichkeit gibt an, wie "sicher" oder "unsicher" ein Ereignis in einem Zufallsexperiment eintritt. Bei mehrfacher Wiederholung kann man so eine Vermutung über den Ausgang des Zufallsexperiments aufstellen.

Bei mehrfachem Werfen eines Würfels werden auf lange Sicht alle Zahlen gleich oft geworfen. Also ist die Wahrscheinlichkeit für jedes Ergebnis 16\frac{1}{6}.

Wichtige Begriffe im Zufallsexperiment

  • Ergebnis: Jeder spezifische Ausgang eines Experiments wird als Ergebnis bezeichnet. Beispiel: Beim Wurf eines Würfels ist der Ausgang "Es fällt eine 3." ein mögliches Ergebnis.

  • Ergebnisraum: Im Ergebnisraum sind alle möglichen Ergebnisse enthalten. Der Ergebnisraum wird häufig mit dem griechischen Buchstaben Ω\Omega ("omega") bezeichnet. Beispiel: Beim Wurf eines Würfels ist der Ergebnisraum Ω={1;2;3;4;5;6} \Omega = \{1;2;3;4;5;6\}.

  • Ereignis: Ein Ereignis kann aus einem oder mehreren Ergebnissen eines Zufallsexperiments bestehen. Beispiel: Beim Wurf eines Würfels ist der Ausgang "es fällt eine ungerade Zahl" ein Ereignis. Es enthält die Ergebnisse "es fällt eine 1","es fällt eine 3", oder "es fällt eine 5". Dieses Ereignis kann als Zahlenmenge geschrieben werden: "es fa¨llt eine ungerade Zahl"={1;3;5}\text{"es fällt eine ungerade Zahl"} = \{1;3;5\}.

  • Wahrscheinlichkeit: Das Ergebnis jedes einzelnen Versuchs ist zufällig. Bei häufiger Wiederholung des gleichen Experiments lassen sich Gesetzmäßigkeiten erkennen. Diese Gesetzmäßigkeiten kann man zur Definition von Wahrscheinlichkeiten benutzen. Beispiel: Bei mehrfachem Werfen eines Würfels werden auf lange Sicht alle Zahlen gleich oft geworfen. Also ist die Wahrscheinlichkeit für jedes Ergebnis 16\frac{1}{6}.

Besondere Zufallsexperimente

Laplace-Experiment

Beispiel: Beim Werfen eines ungezinkten Würfels ist die Wahrscheinlichkeit für jede Seite gleich groß.

Ein Zufallsexperiment bei dem die Wahrscheinlichkeit für jedes Ergebnis gleich groß ist nennt man Laplace-Experiment. Dieser Würfel ist dann ein Laplace-Würfel.

Bernoulli Experiment

Beispiel: Beim Ziehen von Losen kann man entweder einen Treffer oder eine Niete erhalten. Es gibt also genau zwei mögliche Ergebnisse.

Ein Zufallsexperiment bei dem es genau zwei mögliche Ergebnisse gibt nennt man Bernoulli Experiment.

Mehrstufiges Zufallsexperiment

Ein mehrstufiges Zufallsexperiment ist aus mehreren Zufallsexperimenten zusammengesetzt. Mehrstufige Zufallsexperimente nennt man daher auch zusammengesetzte Zufallsexperimente. Auch die Wiederholung desselben Zufallsexperiment ist ein mehrstufiges Zufallsexperiment.

Beispiel: Wiederholtes Werfen eines Würfels

Ergebnismenge bei mehrstufigen Zufallsexperimenten

Als Ergebnismenge verwendet man bei mehrstufigen Zufallsexperimenten meist eine Menge, die sich aus den Ergebnismengen der einzelnen Teil-Experimente ergibt.

Beispiel:

In einem (zweistufigen) Zufallsexperiment wird

  • erst aus einer Urne, in der sich rote, blaue und gelbe Kugeln befinden, eine Kugel gezogen,

Mögliche Ergebnismenge für das erste Teil-Experiment "Ziehen aus der Urne": Ω1={rot;blau;gelb}\Omega_1 = \{\text{rot};\text{blau}; \text{gelb}\}.

Bild 4: Urne

Bild 4: Urne

  • und anschließend eine Münze geworfen.

Mögliche Ergebnismenge für das zweite Teil-Experiment "Werfen einer Münze": Ω2={Z;K}\Omega_2 = \{Z; K\}.

Bild 5: Münze

Bild 5: Münze

Die Ergebnismenge des mehrstufigen Zufallsexperiments ist dann aus den Ergebnissen der einzelnen Experimente zusammengesetzt.

Ω={rot∣Z);(blau∣Z);(gelb∣Z);(rot∣K);(blau∣K);(gelb∣K)}\Omega = \{\text{rot}|Z); (\text{blau}|Z); (\text{gelb}|Z); (\text{rot}|K); (\text{blau}|K);(\text{gelb}|K)\}

Wahrscheinlichkeiten mehrstufiger Zufallsexperimente ermitteln

Wahrscheinlichkeiten im Baumdiagramm

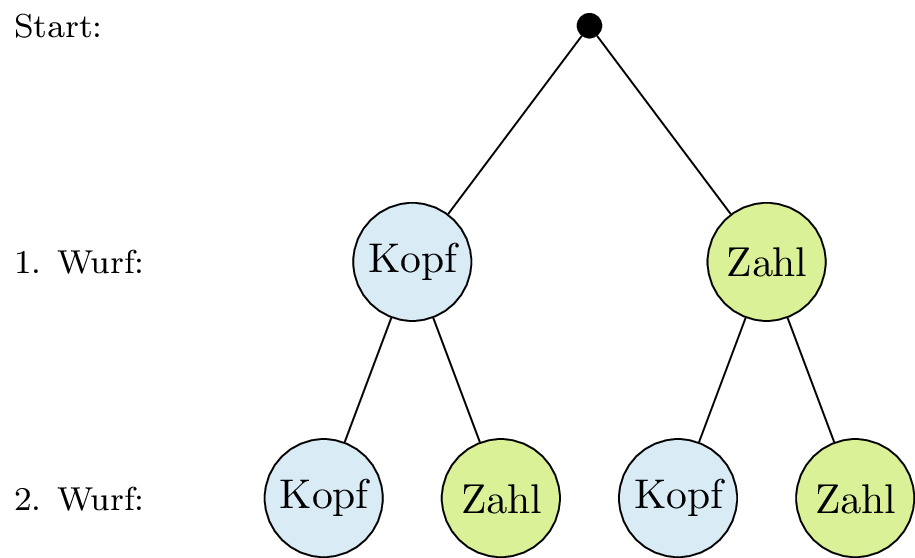
Um die Wahrscheinlichkeit mehrstufiger Zufallsexperimente zu berechnen, verwendet man häufig ein Baumdiagramm.

Mithilfe der Pfadregeln für das Baumdiagramm, ermittelt man die einzelnen Wahrscheinlichkeiten.

Bild

Wahrscheinlichkeiten als Laplace-Wahrscheinlichkeiten

Sind die Wahrscheinlichkeiten aller Ereignisse gleich? Dann kann man das mehrstufige Zufallsexperiment als Laplace-Experiment behandeln.

Die Wahrscheinlichkeit kann man dann mithilfe der Laplace-Wahrscheinlichkeiten berechnen.

Übungsaufgaben: Zufallsexperiment

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Quellen


    Dieses Werk steht unter der freien Lizenz
    CC BY-SA 4.0 → Was bedeutet das?