Eine Figur ist drehsymmetrisch, wenn du sie um sich selbst so drehen kannst, dass sie wieder gleich aussieht. Dabei ist die Figur aber nicht drehsymmetrisch, wenn sie erst bei einer vollständigen Drehung um 360° genauso aussieht.
Kriterium für Drehsymmetrie
Eine Figur ist drehsymmetrisch, wenn sie nach einer Drehung um einen Drehpunkt um einen Winkel (mit ) auf sich selbst abgebildet wird (d.h. genau so aussieht wie zuvor). Der Drehpunkt kann dabei auch als der Flächenschwerpunkt der Figur gesehen werden.
Oft sagt man auch, dass die Figur 2-zählig, 3-zählig, 4-zählig, .... drehsymmetrisch ist, wenn man die Figur 2 bzw., 3 oder 4 mal drehen kann bis die Ausgangslage der Figur erreicht ist.
Allgemein ist eine Figur n-zählig drehsymmetrisch, falls gilt.
Drehsymmetrie im Alltag
Drehsymmetrische Figuren begegnet man nicht nur in der Mathematik, sondern auch im Alltag findet man drehsymmetrische Figuren.
Im Folgenden siehst du Objekte aus den Alltag, die drehsymmetrisch sind:

Jedoch muss man sich bei den drehsymmetrischen Objekten in der Natur (z.B. Blumen, Schneeflocken, Früchte ect.) bewusst sein, dass sie nicht zu 100% drehsymmetrisch sind.
Drehsymmetrische Figuren
Im Folgenden siehst du Figuren, die drehsymmetrisch sind:
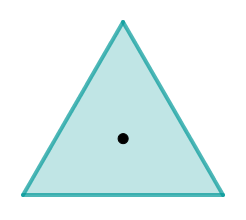
Bei einer Drehung um 120° wird das gleichseitige Dreieck exakt gleich abgebildet. Das gleichseitige Dreieck ist 3-zählig drehsymmetrisch, da
. Das heißt das Dreieck wird auch bei einer Drehung um 240° und 360° wieder auf sich selbst abgebildet.
Bei einer Drehung um 90° wird die Figur exakt gleich abgebildet. Die Figur ist 4-zählig drehsymmetrisch, da
. Das heißt die Figur wird auch bei einer Drehung um 180°, 270° und 360° wieder auf sich selbst abgebildet.

Bei einer Drehung um 90° wird die Figur exakt gleich abgebildet. Die Figur ist 4-zählig drehsymmetrisch, da
Das heißt, die Figur wird auch bei einer Drehung um 180°, 270° und 360° wieder auf sich selbst abgebildet.
ACHTUNG: Bei einer Drehung um 45° wird die Figur aufgrund der Farben nicht auf sich selbst abgebildet.

Bestimmung der Drehsymmetrie einer Figur
Um die Drehsymmetrie einer Figur zu untersuchen, befolgen wir folgende 3 Schritte:
Schritt 1: Bestimmung des Drehpunkts
Der Drehpunkt ist der Flächenschwerpunkt der Figur. Jedoch ist es nicht immer einfach, den Drehpunkt einer Figur zu bestimmen. Bei einigen Figuren ist es einfacher als bei anderen.
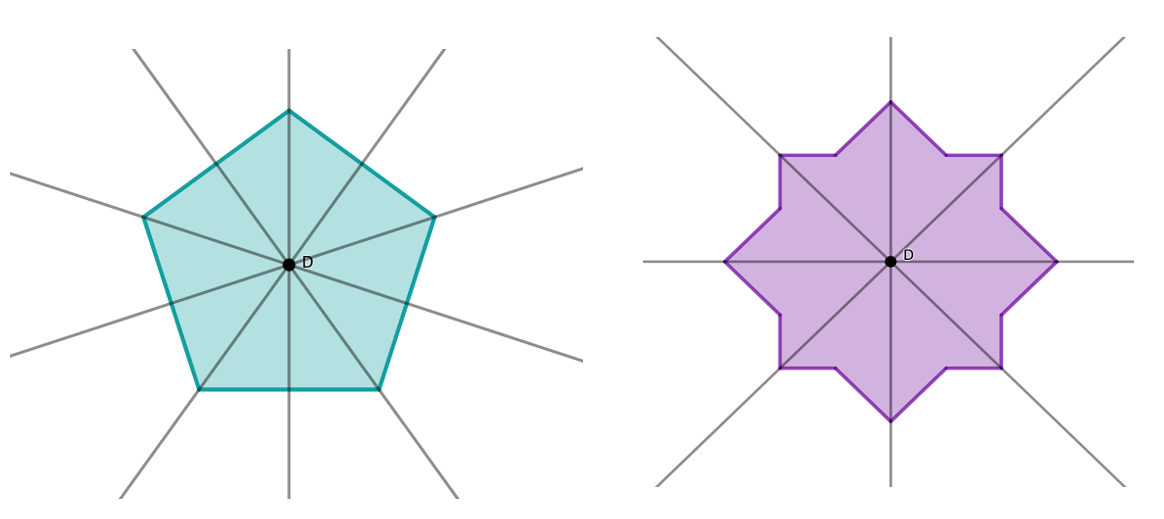
Zum Beispiel kann man den Drehpunkt eines regelmäßigen Fünfecks bestimmen, in dem man die Seitenhalbierende der einzelnen Seiten einzeichnet. Der Schnittpunkt dieser Seitenhalbierenden bestimmt ist der Drehpunkt. Mit dieser Vorgehensweise kann man auch den Drehpunkt eines regelmäßigen Dreiecks, Siebenecks etc. bestimmen.
Um den Drehpunkt eines regelmäßigen Sechsecks zu bestimmen, verbindet man die gegenüberliegenden Ecken durch eine Gerade miteinander und der Schnittpunkt dieser Geraden liefert den Drehpunkt. Mithilfe dieser Vorgehensweise kann man auch den Drehpunkt eines regelmäßigen Vierecks, Achtecks etc. bestimmen.
Wenn der Drehwinkel beträgt, ist die Figur punktsymmetrisch. Wenn du je zwei Punkte, die aufeinander abgebildet werden, mit einer Strecke verbindest, ist der Schnittpunkt dieser beiden Strecken der Drehpunkt.
Allgemein kannst du es so machen, dass du dir drei Punkte suchst, die aufeinander abgebildet werden. Wenn du je zwei von diesen verbindest und die Mittelsenkrechten der Verbindungsstrecken einzeichnest, schneiden die sich im Drehpunkt.
Schritt 2: Bestimmung des Drehwinkels
Den Drehwinkel erhältst du, indem du zunächst einen Kreis um den ermittelten Drehpunkt ziehst. Wobei der Radius die Strecke zwischen dem Drehpunkt und einer Ecke ist.
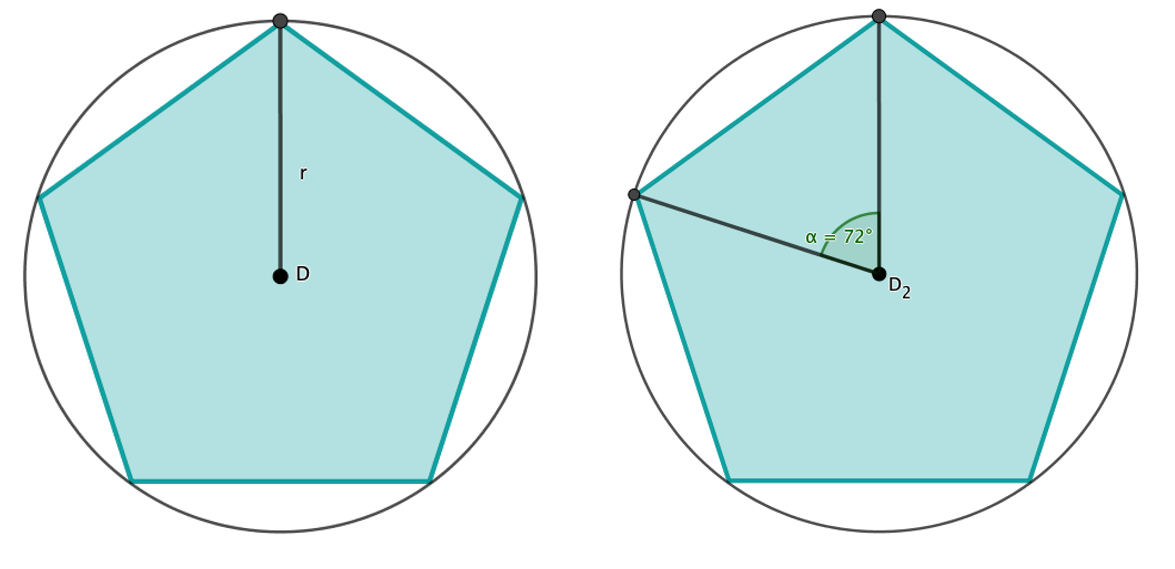
Der Drehwinkel eines Fünfecks beträgt .
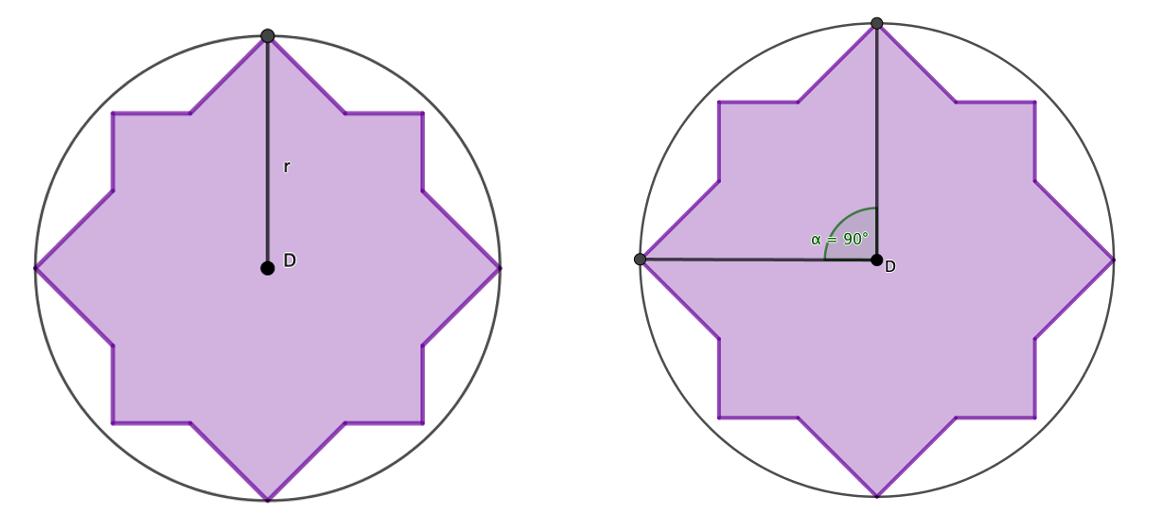
Der Drehwinkel der oben dargestellten Figur beträgt .
Schritt 3: Bestimmung der n-zähligen Drehsymmetrie der Figur
Die zu Beginn des Artikel dargestellte Formel, kann man wie folgt umformen:
Also ist das Fünfeck 5-zählig drehsymmetrisch, denn . Das Fünfeck wird auch bei einer Drehung um 144°, 216°, 288° und 360° wieder auf sich selbst abgebildet.
Die andere Figur ist 4-zählig drehsymmetrisch, denn . Die Figur wird auch bei einer Drehung um 180°, 270° und 360° wieder auf sich selbst abgebildet.
Unterschied zwischen Drehsymmetrie und Punktsymmetrie
Die Punktsymmetrie ist ein Spezialfall der Drehsymmetrie. Eine Figur heißt punktsymmetrisch, wenn sie nach einer Drehung um einen Drehpunkt um den Winkel auf sich selbst abgebildet wird. Also sind punktsymmetrische Figuren 2-zählig drehsymmetrisch.
Jede punktsymmetrische Figur ist auch drehsymmetrisch.
Die dargestellte Spielkarte ist punktsymmetrisch bezüglich des rot eingezeichneten Punkts. Dreht man die Spielkarte um 180° um den roten Punkt, so wird die Spielkarte wieder auf sich selbst abgebildet.
Außerdem ist die Karte 2-zählig drehsymmetrisch, da man die Karte zweimal drehen kann bis sie ihre Ausgangslage erreicht hat und es gilt
.

Übungsaufgaben
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
