Punktsymmetrie

Eine Figur heißt punktsymmetrisch, wenn sie durch die Spiegelung an einem Punkt, dem sogenannten Symmetriepunkt oder Symmetriezentrum, auf sich selbst abgebildet wird.

Es handelt sich um eine Drehung der Figur um 180°.

Punktsymmetrische Figuren

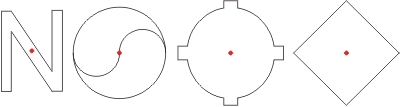
Die jeweils rot gekennzeichneten Punkte sind die Symmetriepunkte der Figuren.

Parallelogramm

Ein Parallelogramm ist ein Viereck, in dem gegenüberliegende Seiten parallel zueinander liegen.

Kreis

Ein Kreis ist eine geschlossene Linie um einen Mittelpunkt $M$ . Alle Punkte auf der Linie haben den gleichen Abstand/Radius zum Mittelpunkt.

Punktsymmetrie bei Funktionen

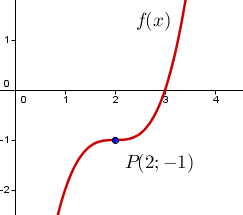
DefinitionPunktsymmetrie bei Funktionen

Der Graphen einer Funktion ist punktsymmetrisch zum Punkt $P=(x_0,y_0)$ , wenn $f(x_0-x)-y_0=-f(x_0+x)+y_0$ .

Beispiel

Die Funktion $f\left(x\right)=\left(x-2\right)^3-1$ ist punktsymmetrisch zum Punkt $P(2|-1)$ , da

\displaystyle f(2-x)-(-1)=(2-x-2)^3-1+1=-x^3

und

\displaystyle f(2-x)-(-1)=(2-x-2)^3-1+1=-x^3

ist.

Geogebra File: https://assets.serlo.org/legacy/8870_BNJuhm1LmI.xml

Ein Spezialfall ist die Punktsymmetrie am Ursprung, also für $P=(0{,}0)$ . Die Gleichung vereinfacht sich, dann zu:

\displaystyle f(2-x)-(-1)=(2-x-2)^3-1+1=-x^3

Punktspiegelung

Um eine beliebige Figur $F$ an einem Punkt $P$ zu spiegeln, werden nacheinander alle charakteristischen Punkte an $P$ gespiegelt und schließlich entsprechend der Gestalt von $F$ verbunden.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/1520487]

Übungsaufgaben: Punktsymmetrie

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Erkennen und Beschreiben von symmetrischen Körpern

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?