Ein Teilstück einer Langlaufloipe verläuft von oben betrachtet geradlinig und hat im Querschnitt das abgebildete Profil, welches annähernd durch den Graphen der Funktion mit der Definitionsmenge beschrieben werden kann. Die -Achse gibt die Länge in waagrechter Richtung an, auf der -Achse ist die Höhe über dem Meeresspiegel aufgetragen. Die Koordinaten und stellen Längenangaben in der Einheit Kilometer bzw. Meter dar.
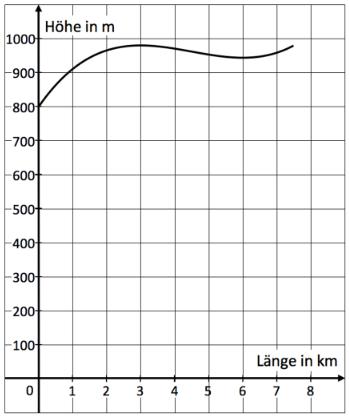
Ermitteln Sie die maximalen Teilintervalle von , in denen die Loipe auf- bzw. abwärts verläuft.
Berechnen Sie unter Verwendung von Teilaufgabe a), in welcher horizontalen Entfernung vom Beginn des Teilstückes der Loipe maximale Höhe erreicht wird. Geben Sie an, in welcher Höhe Sporttreibende sich am höchsten Punkt der Loipe befinden.
Ermitteln Sie, nach wie vielen Kilometern in horizontaler Entfernung vom Ausgangspunkt die Loipe am steilsten abwärts verläuft.
Bestimmen Sie die durchschnittliche Steigung der Loipe in Prozent auf den ersten drei Kilometern.
Die Steigung der Loipe bei Kilometer 2 tritt im weiteren Verlauf der Loipe noch einmal auf. Berechnen Sie die Stelle, an der dies der Fall ist.
