Teil 2 Analysis II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Ein Teilstück einer Langlaufloipe verläuft von oben betrachtet geradlinig und hat im Querschnitt das abgebildete Profil, welches annähernd durch den Graphen der Funktion $f: x \rightarrow 8\cdot \left(\dfrac{1}{3}x^3-\dfrac{9}{2}x^2+18x+100\right)$ mit der Definitionsmenge $\mathbb{D_f}=\left[0;7{,}5\right]$ beschrieben werden kann. Die $x$ -Achse gibt die Länge in waagrechter Richtung an, auf der $y$ -Achse ist die Höhe über dem Meeresspiegel aufgetragen. Die Koordinaten $x$ und $y$ stellen Längenangaben in der Einheit Kilometer bzw. Meter dar.
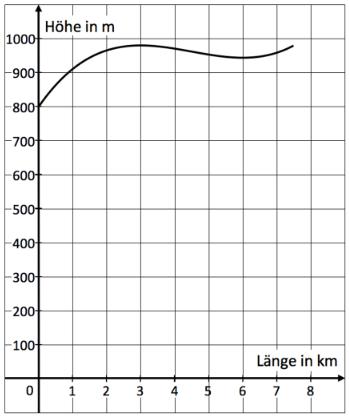
1. Ermitteln Sie die maximalen Teilintervalle von $\mathbb{D_f}$ , in denen die Loipe auf- bzw. abwärts verläuft.
2. Berechnen Sie unter Verwendung von Teilaufgabe a), in welcher horizontalen Entfernung vom Beginn des Teilstückes der Loipe maximale Höhe erreicht wird. Geben Sie an, in welcher Höhe Sporttreibende sich am höchsten Punkt der Loipe befinden.
3. Ermitteln Sie, nach wie vielen Kilometern in horizontaler Entfernung vom Ausgangspunkt die Loipe am steilsten abwärts verläuft.
4. Bestimmen Sie die durchschnittliche Steigung der Loipe in Prozent auf den ersten drei Kilometern.
5. Die Steigung der Loipe bei Kilometer 2 tritt im weiteren Verlauf der Loipe noch einmal auf. Berechnen Sie die Stelle, an der dies der Fall ist.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
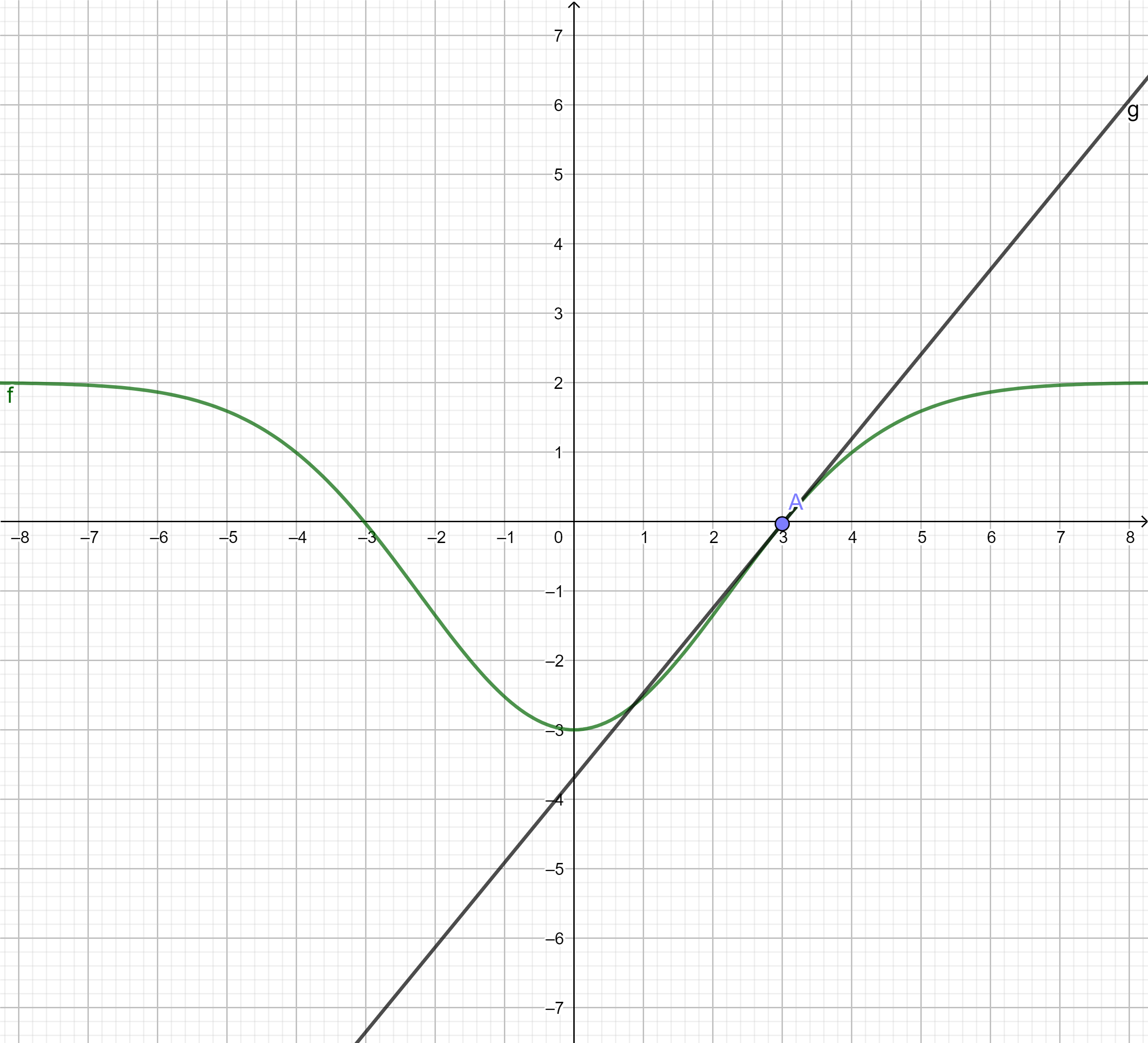
Gegeben ist die Funktion $g: x \rightarrow2-5e^{-0{,}1x^2}$ mit der Definitionsmenge $D_g= \mathbb{R}$ . Der Graph von g in einem kartesischen Koordinatensystem wird mit $G_g$ bezeichnet.
1. Untersuchen Sie das Symmetrieverhalten des Graphen $G_g$ bezüglich des Koordinatensystems sowie das Verhalten der Funktionswerte von g für $|x|→ \infty$ . Geben Sie die Gleichung der Asymptote des Graphen $G_g$ an.
2. Berechnen Sie die Nullstellen von g. Runden Sie auf zwei Nachkommastellen.
3. Ermitteln Sie Art und Koordinaten des relativen Extrempunktes von $G_g$ . Begründen Sie, warum dieser absolut ist und geben Sie die Wertemenge $W_g$ der Funktion g an.
  [Teilergebnis: $g'(x)=x\cdot e^{-0{,}1x^2}$ ]
4. Stellen Sie die Gleichung der Tangente an $G_g$ an der Stelle $x=3$ in allgemeiner Form auf.
5. Art und Koordinaten des relativen Extrempunktes von $G_g$ können auch ohne Verwendung der Ableitungsfunktion bestimmt werden. Begründen Sie dies mithilfe bekannter Ergebnisse. Verwenden Sie dabei die Tatsache, dass nur höchstens ein Extrempunkt von $G_g$ existiert.
6. Zeichnen Sie unter Verwendung aller bisheriger Ergebnisse und weiterer geeigneter Funktionswerte den Graphen der Funktion g im Bereich $-7 \leq x \leq7$ in ein kartesisches Koordinatensystem.
  Maßstab für beide Achsen: 1 LE = 1 cm

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?