Gegeben ist die Funktion mit der Definitionsmenge . Der Graph von g in einem kartesischen Koordinatensystem wird mit bezeichnet.
Untersuchen Sie das Symmetrieverhalten des Graphen bezüglich des Koordinatensystems sowie das Verhalten der Funktionswerte von g für . Geben Sie die Gleichung der Asymptote des Graphen an.
Berechnen Sie die Nullstellen von g. Runden Sie auf zwei Nachkommastellen.
Ermitteln Sie Art und Koordinaten des relativen Extrempunktes von . Begründen Sie, warum dieser absolut ist und geben Sie die Wertemenge der Funktion g an.
[Teilergebnis: ]
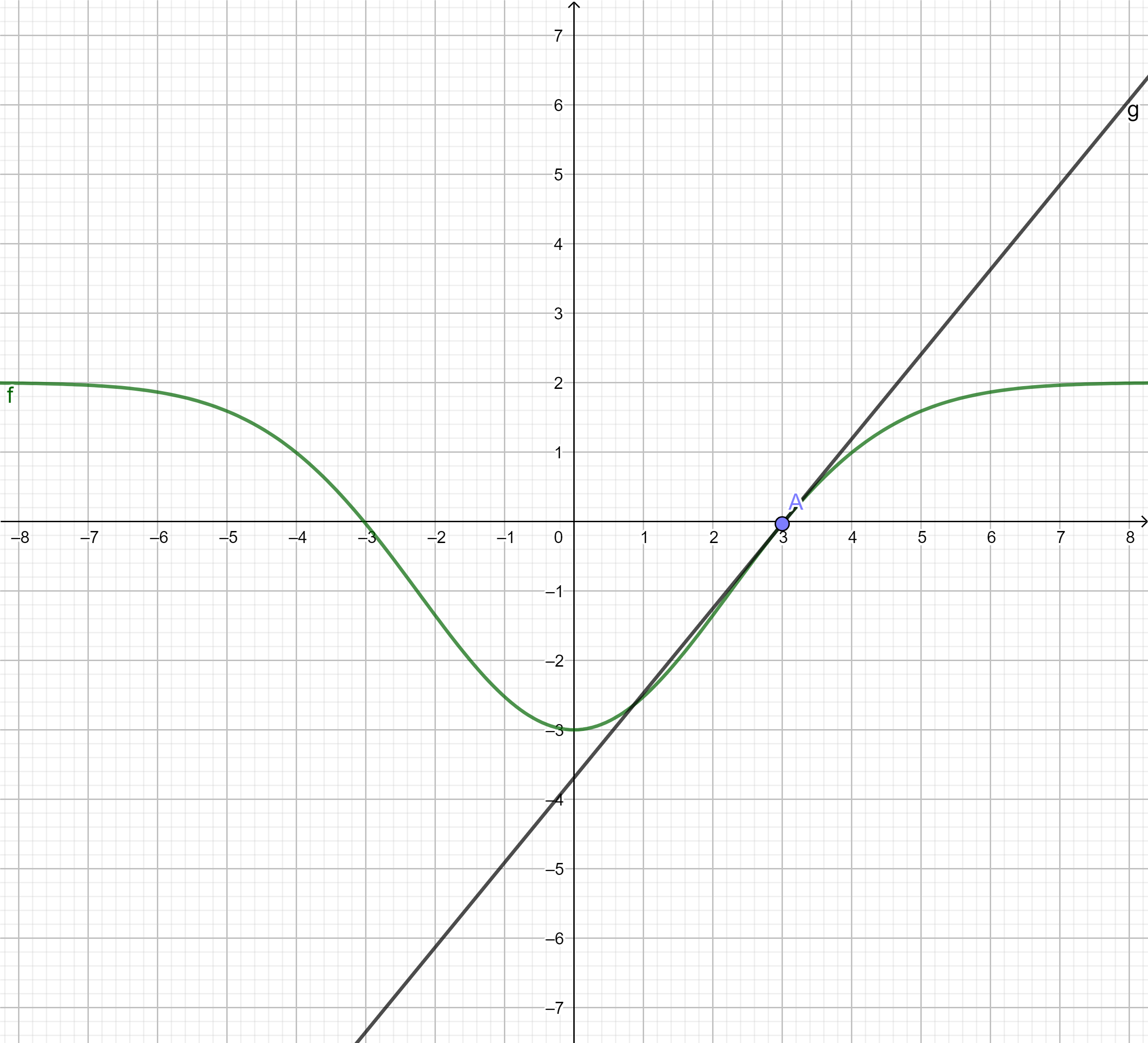
Stellen Sie die Gleichung der Tangente an an der Stelle in allgemeiner Form auf.
Art und Koordinaten des relativen Extrempunktes von können auch ohne Verwendung der Ableitungsfunktion bestimmt werden. Begründen Sie dies mithilfe bekannter Ergebnisse. Verwenden Sie dabei die Tatsache, dass nur höchstens ein Extrempunkt von existiert.
Zeichnen Sie unter Verwendung aller bisheriger Ergebnisse und weiterer geeigneter Funktionswerte den Graphen der Funktion g im Bereich in ein kartesisches Koordinatensystem.
Maßstab für beide Achsen: 1 LE = 1 cm