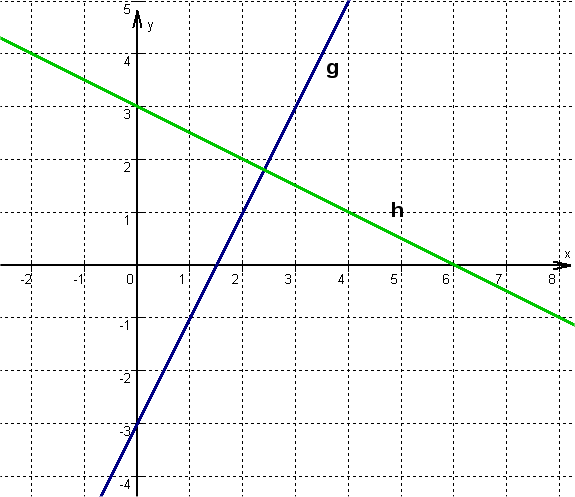
Gegeben sind die Geraden und .
Überprüfe, ob die Punkte , , , und auf einer der Geraden liegen.
Ergänze die Koordinaten so, dass die Punkte auf h liegen: P(5 | ?) , Q(-3,5 | ?) , R(? | 12) , S(? | -7,5).
Zeige, dass T(2,4|1,8) auf beiden Geraden liegt. Was bedeutet dies?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?