Goldener Schnitt

Das Verhältnis des „Goldenen Schnitts“

Der „Goldene Schnitt“ ist ein Verhältnis, das vorliegt, wenn von zwei Seiten die längere Seite zur kürzeren Seite, genau das gleiche Verhältnis hat, wie die beiden Seitenlängen addiert zur längeren Seite. In Formeln bedeutet das:

Setzt man $\frac{\mathrm a}{\mathrm b}=\mathrm\Phi$ in die Gleichung ein, erhält man:

Bringt man alles auf eine Seite und multipliziert die Gleichung mit $\mathrm\Phi$, ergibt sich:

Mit der Mitternachtsformel erhält man dann:

Die zweite, negative Lösung ergeben für Streckenlängen keinen Sinn und kann vernachlässigt werden.

Der „Goldene Schnitt“

Man sagt, der „Goldene Schnitt“ sei für den Menschen das schönste Verhältnis. Es wird daher oft in Architektur und Kunst verwendet.

Welches Rechteck ist am schönsten?

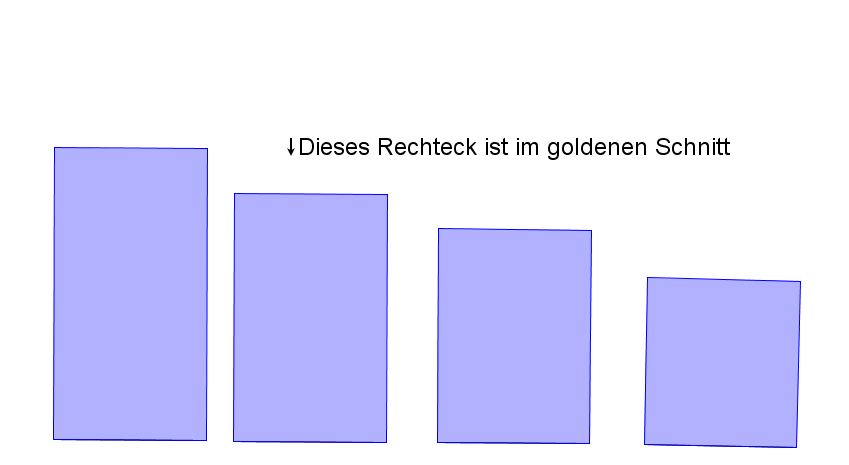
Rechnen mit dem goldenen Schnitt

Der goldene Schnitt besitzt auch einige interessante Recheneigenschaften:

• $\mathrm\Phi^2=\mathrm\Phi+1$

• $\frac1{\mathrm\Phi}=\mathrm\Phi-1$

DinA4

Entgegen der weit verbreiteten Meinung ist Papier nach deutschem Industrienorm nicht im „Goldenen Schnitt“. Es steht in einem anderen Verhältnis, das ebenfalls eine interessante Eigenschaft hat. Halbiert man DIN Papier an der längeren Seite, erhält man wieder DIN Papier eine Größe kleiner. Das tatsächliche Seitenverhältnis beträgt $\sqrt{2}$.

Goldener Schnitt und Fibonacci

Die Fibonaccizahlen, sind eine spezielle Zahlenreihe, die man vielleicht aus „Sakrileg“ kennt.

Die ursprüngliche Aufgabe war:

Man hat ein Kaninchenpaar. Jedes Kaninchenpaar bekommt jeden Monat ein weiteres Kaninchenpaar als Kinder, allerdings erst ab dem 2. Monat, da ein neugeborenes Paar noch zu jung ist. Man startet mit einem Kaninchenpaar, das gerade geboren wurde. Wie viele Kaninchenpaare hat man am Ende jedes Monats.

Aus dieser Aufgabe ergibt sich folgende Zahlenreihe:

$1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,…$

Man erhält die nächste Zahl dadurch, dass man die vorhergehenden Zahlen addiert.

Den „Goldenen Schnitt“ erhält man in einer Näherung, indem man eine Fibonaccizahl, durch die vorhergehende Zahl teilt.

Ab $55$ ist der Fehler bereits kleiner als $1\;\%$.

Goldener Schnitt und Konstruktion eines regelmäßigen 5 Ecks Artikel zum Thema