Steckbriefaufgabe

Gegenstand einer Steckbriefaufgabe ist die exakte Bestimmung eines Funktionsterms anhand von vorgegebenen Informationen (z.B. Position von Nullstellen, Hochpunkten etc.).

Dieser Artikel behandelt nur Funktionsterme in Form von Polynomen.

Eine beispielhafte Aufgabe wäre:

Finde eine Funktion $2$ . Grades, die eine doppelte Nullstelle bei $x_{0} = 1$ besitzt und durch den Punkt $P (0 | 1) |$ verläuft.

Beispiel

Im folgenden Video siehst du ein Beispiel für eine Steckbriefaufgabe und wie du sie lösen kannst.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von YouTube geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://youtu.be/-C3227uS794]

Der allgemeine Ansatz

Als erste Information benötigt man den Grad der zu bestimmenden Funktion. Davon ausgehend, lässt sich die allgemeine Funktionsgleichung $f (x) = a x^{n} + b x^{n - 1} + \dots$ aufstellen. Ziel ist es nun, die Unbekannten $a$ , $b$ , $\dots$ zu bestimmen. Dazu sind mehrere Informationen erforderlich, die jeweils unterschiedliche Gleichungen liefern. Zum Beispiel resultiert aus der Information, dass ein gegebener Punkt $P (x_{0}, y_{0})$ auf dem Funktionsgraphen liegt, die Gleichung

a \cdot x_{0}^{n} + b \cdot x_{0}^{n - 1} + \dots = y_{0}

Mehrere Bedingungen führen zu mehreren Gleichungen, die zusammen ein lineares Gleichungssystem ergeben, dessen Lösung die Koeffizienten $a$ , $b$ , $\dots$ sind.

Von der Information zur Gleichung

Ein großer Teil der Arbeit bei dieser Problemstellung liegt im Aufstellen der zu einer Information zugehörigen Gleichungen. In der folgenden Tabelle steht links jeweils die gegebene Information, in der Mitte die allgemeine Gleichung, die daraus resultiert und rechts ein erläuterndes Beispiel.

In den folgenden drei Abschnitten wird hinsichtlich der Anzahl an Gleichungen, die eine Information liefert, unterschieden.

Einfache Information

Sei die allgemeine Funktion f beispielhaft vom Grad $3$ :

$f (x) = a x^{3} + b x^{2} + c x + d$
$f^{'} (x) = 3 a x^{2} + 2 b x + c$
$f^{''} (x) = 6 a x + 2 b$

Information	allgemeine Gleichung (am Beispiel von Gleichungen vom Grad 3)	Beispiel
$f$ besitzt eine Nullstelle ( $f (x) = 0$ ) bei $N_{1}$	$a \cdot N_{1}^{3} + b \cdot N_{1}^{2} + c \cdot N_{1} + d = 0$	$N_{1} = 2 :$ $a \cdot 8 + b \cdot 4 + c \cdot 2 + d = 0$
$G_{f}$ verläuft durch $P = (p_{x}, p_{y})$	$a \cdot p_{x}^{3} + b \cdot p_{x}^{2} + c \cdot p_{x} + d = p_{y}$	$P = (2,3)$ : $a \cdot 8 + b \cdot 4 + c \cdot 2 + d = 3$
$f$ hat eine Extremstelle ( $f^{'} (x) = 0$ ) bei $E_{1}$	$3 a \cdot E_{1}^{2} + 2 b \cdot E_{1} + c = 0$	$f^{'} (2) = 0 :$ $3 a \cdot 4 + 2 b \cdot 2 + c = 0$
$f$ hat eine Wendestelle ( $f^{''} (x) = 0$ ) bei $W_{1}$	$6 a \cdot W_{1} + 2 b = 0$	$f^{''} (2) = 0$ : $6 a \cdot 2 + 2 b = 0$

Beispiel - Polynom vom Grad 2

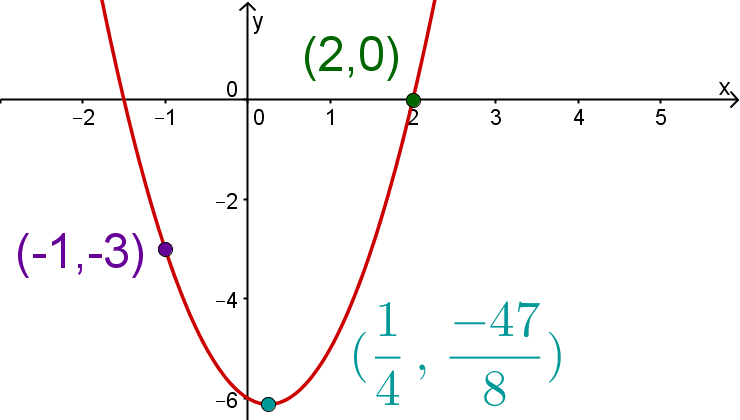
Gesucht ist eine Funktion vom Grad 2, die eine Nullstelle bei $x = 2$ besitzt, durch den Punkt $P (- 1, - 3)$ verläuft und ein Minimum bei $x = \frac{1}{4}$ besitzt.

Im Folgenden sind die Informationen mit den jeweils resultierenden Gleichungen dargestellt:

Information	Mathematische Beschreibung	Gleichung
Funktion vom Grad $2$	$f (x) = a x^{2} + b x + c$ $f^{'} (x) = 2 a x + b$
Besitzt eine Nullstelle bei $x = 2$	$f (2) = 0$	$a \cdot 4 + b \cdot 2 + c = 0$
Verläuft durch den Punkt $P (- 1; - 3)$	$f (- 1) = - 3$	$a \cdot (- 1)^{2} + b \cdot (- 1) + c = - 3$
Besitzt ein Minimum bei $x = \frac{1}{4}$	$f^{'} (\frac{1}{4}) = 0$	$2 \cdot a \cdot \frac{1}{4} + b = 0$

Daraus ergibt sich folgendes Gleichungssystem:

\begin{array}{cccccccc} (I) & 4 a & + & 2 b & + & 1 c & = & 0 \\ (I I) & 1 a & - & 1 b & + & 1 c & = & - 3 \\ (I I I) & \frac{1}{2} a & + & 1 b & + & 0 c & = & 0 \end{array}

mit der eindeutigen Lösung

$a = 2$ , $b = - 1$ , $c = - 6$

also hat $f$ die Form

f (x) = 2 x^{2} - x - 6

Mehrfache Information

Viele Aussagen verraten uns mehrere Informationen auf einmal.

Die folgende Tabelle stellt die Aussagen den eigentlichen Informationen gegenüber.

Aussage	Einfache Informationen
$f$ besitzt eine doppelte Nullstelle bei $N_{1}$	$f$ besitzt eine Nullstelle bei $N_{1} : f (N_{1}) = 0$ $f$ besitzt eine Extremstelle bei $N_{1} : f^{'} (N_{1}) = 0$
$f$ besitzt einen Extrempunkt bei $P (x_{0} \| y_{0}) \|$	$f$ verläuft durch den Punkt $P :$ $f (x_{0}) = y_{0}$ $f$ besitzt eine Extremstelle bei $P : f^{'} (x_{0}) = 0$
$f$ besitzt einen Wendepunkt bei $P (x_{0}, y_{0})$	$f$ verläuft durch den Punkt $P : f (x_{0}) = y_{0}$ $f$ besitzt eine Wendestelle bei $P : f^{''} (x_{0}) = 0$
$f$ besitzt eine Sattelstelle bei $S (x_{0}, y_{0})$	$f (x_{0}) = y_{0}$ $f^{'} (x_{0}) = 0$ $f^{''} (x_{0}) = 0$

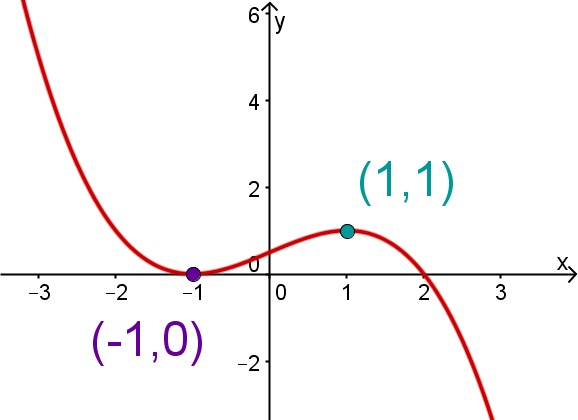
Beispiel - Polynom vom Grad 3

Formulierung	Mathematische Bedeutung
Gesucht ist eine Funktion vom Grad $3$ ,	$f (x) = a x^{3} + b x^{2} + c x + d$ , $f^{'} (x) = 3 a x^{2} + 2 b x + c$ , $f^{''} (x) = 6 a x + 2 b$
die eine doppelte Nullstelle bei $N_{1} = - 1$	$a \cdot (- 1)^{3} + b \cdot (- 1)^{2} + c \cdot (- 1) + d = 0$ $3 a \cdot (- 1)^{2} + 2 b \cdot (- 1) + c = 0$
und einen Extrempunkt bei $E (1 \| 1)$ hat.	$a \cdot 1^{3} + b \cdot 1^{2} + c \cdot 1 + d = 1$ $3 a \cdot 1^{2} + 2 b \cdot 1 + c = 0$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{ccccc} - 1 a & + 1 b & - 1 c & + 1 d & = 0 \\ 3 a & - 2 b & + 1 c & + 0 d & = 0 \\ 3 a & + 2 b & + 1 c & + 0 d & = 0 \\ a & + 1 b & + 1 c & + 1 d & = 1 \end{array}$

mit der eindeutigen Lösung

$a = - \frac{1}{4}, b = 0, c = \frac{3}{4}, d = \frac{1}{2}$

also hat $f$ die Form

f (x) = - \frac{1}{4} x^{3} + \frac{3}{4} x + \frac{1}{2}

Besondere Informationen

Aus manchen Informationen resultieren noch stärkere Aussagen als die bisher beschriebenen.

Information	Auswirkung	Beispiel
$f$ ist achsensymmetrisch zur $y$ -Achse	alle Variablen vor ungeraden Potenzen von $x$ entfallen	$f (x) = a x^{4} + b x^{3} + c x^{2} + d x + e$ wird zu $f (x) = a x^{4} + c x^{2} + e$
$f$ ist punktsymetrisch zum Ursprung	alle Variablen vor geraden Potenzen von $x$ entfallen	$f (x) = a x^{3} + b x^{2} + c x + d$ wird zu $f (x) = a x^{3} + c x$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?