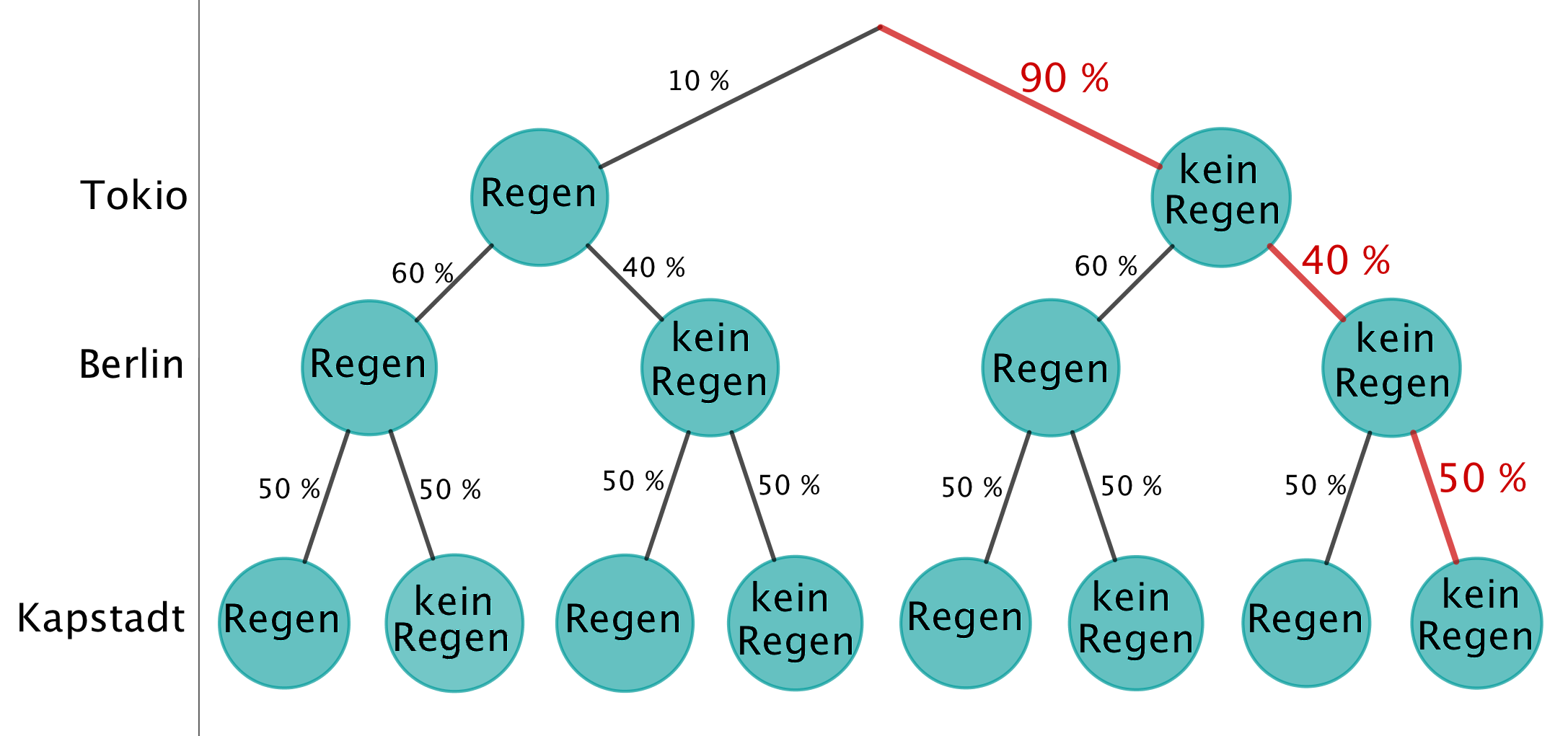
Für ein WM-Endspiel finden in Berlin, Kapstadt und Tokio Public-Viewing-Veranstaltungen statt. Im Internet findet man folgende Vorhersage, die sich auf das Wetter während des Spiels bezieht:

Zum Beispiel bedeutet die Angabe „“: Die Wahrscheinlichkeit dafür, dass es während des Spiels in Berlin mindestens einmal regnet (z. B. in Form eines Schauers), beträgt .
Geben Sie die Wahrscheinlichkeit dafür an, dass es während des Spiels in Tokio nicht regnet. (1 BE)
Berechnen Sie die Wahrscheinlichkeit (in Prozent) dafür, dass es während des Spiels in keiner dieser drei Städte regnet. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?