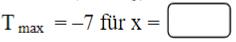Ergänze die beiden Kästchen so, dass eine wahre Aussage entsteht ().
Der Term
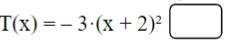
hat den Extremwert
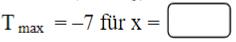
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Ergänze die beiden Kästchen so, dass eine wahre Aussage entsteht ().
Der Term
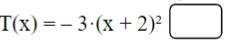
hat den Extremwert