Gegeben ist die in definierte Funktion . Die Abbildung zeigt den Graphen von f.
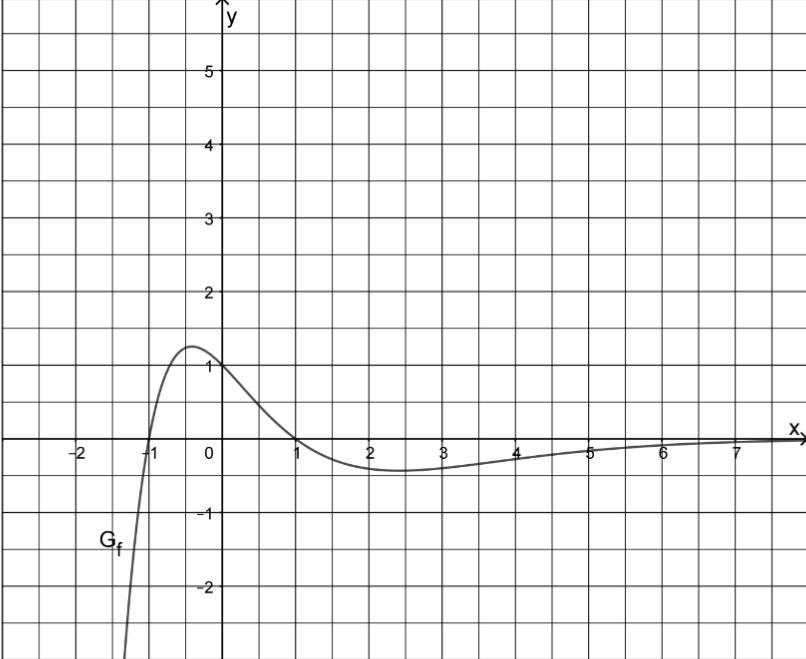
Zeigen Sie, dass genau zwei Nullstellen besitzt. (2P)
Bestimmen Sie rechnerisch die x-Koordinaten der beiden Extrempunkte von . (4P)
(zur Kontrolle: )
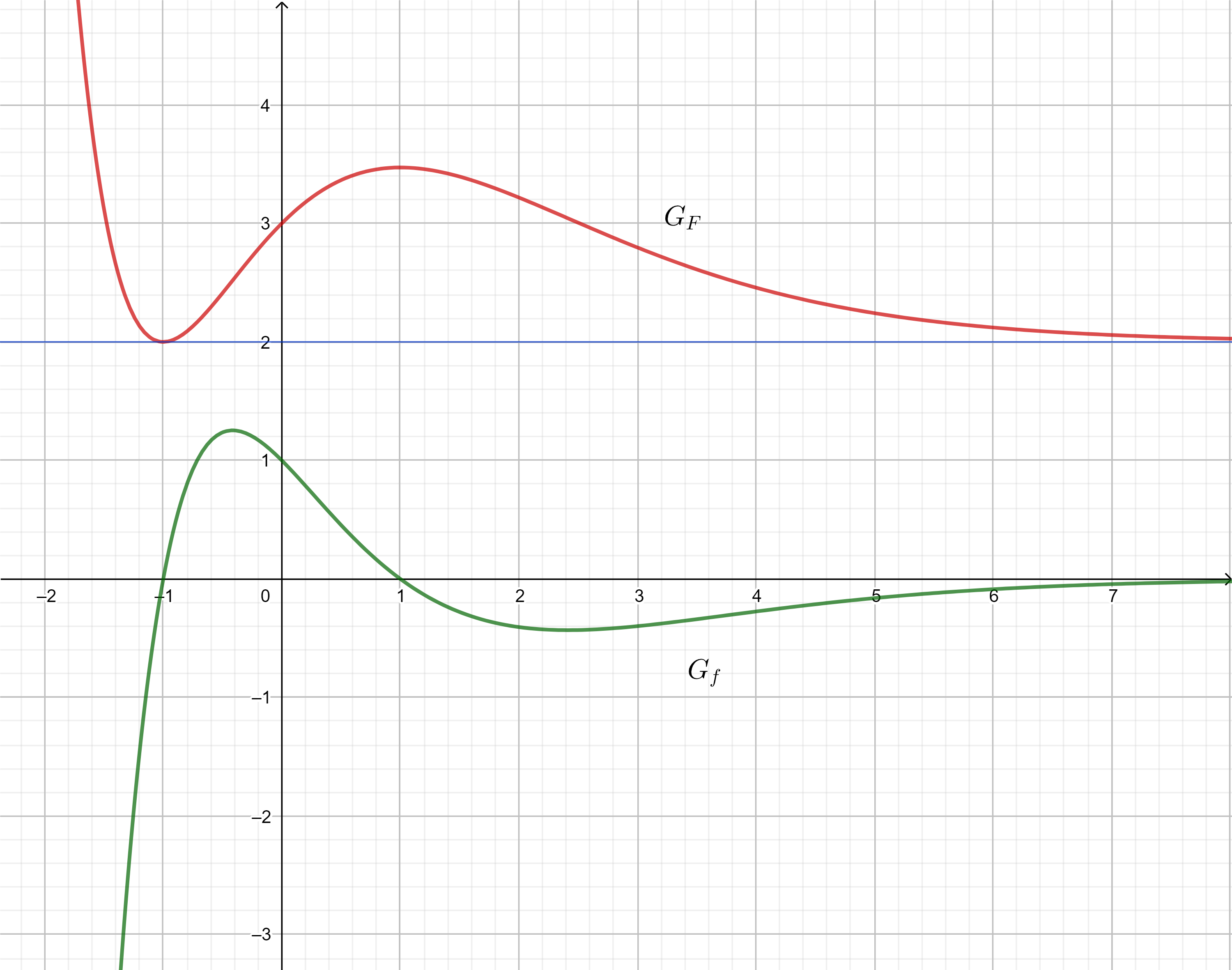
Ermitteln Sie anhand der Abbildung einen Näherungswert für das Integral . (4P)
Die in definierte Funktion ist diejenige Stammfunktion von , deren Graph durch den Punkt verläuft.
Begründen Sie mithilfe der Abbildung, dass der Graph von im Punkt einen Tiefpunkt besitzt. (2P)
Skizzieren Sie in der Abbildung den Graphen von . Berücksichtigen Sie dabei insbesondere, dass und gilt. (3P)
Deuten Sie die Aussage in Bezug auf geometrisch. (2P)
Betrachtet wird nun die Schar der in definierten Funktionen
mit . Der Graph von wird mit bezeichnet. Für ergibt sich die bisher betrachtete Funktion .
Geben Sie in Abhängigkeit von die Anzahl der Nullstellen von an. (2P)
Für einen bestimmten Wert von besitzt zwei Schnittpunkte mit der x-Achse, die voneinander den Abstand haben. Berechnen Sie diesen Wert. (3P)
Beurteilen Sie, ob es einen Wert von gibt, sodass und bezüglich der x-Achse symmetrisch zueinander liegen. (2P)