Analysis, Teil B, Aufgabengruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
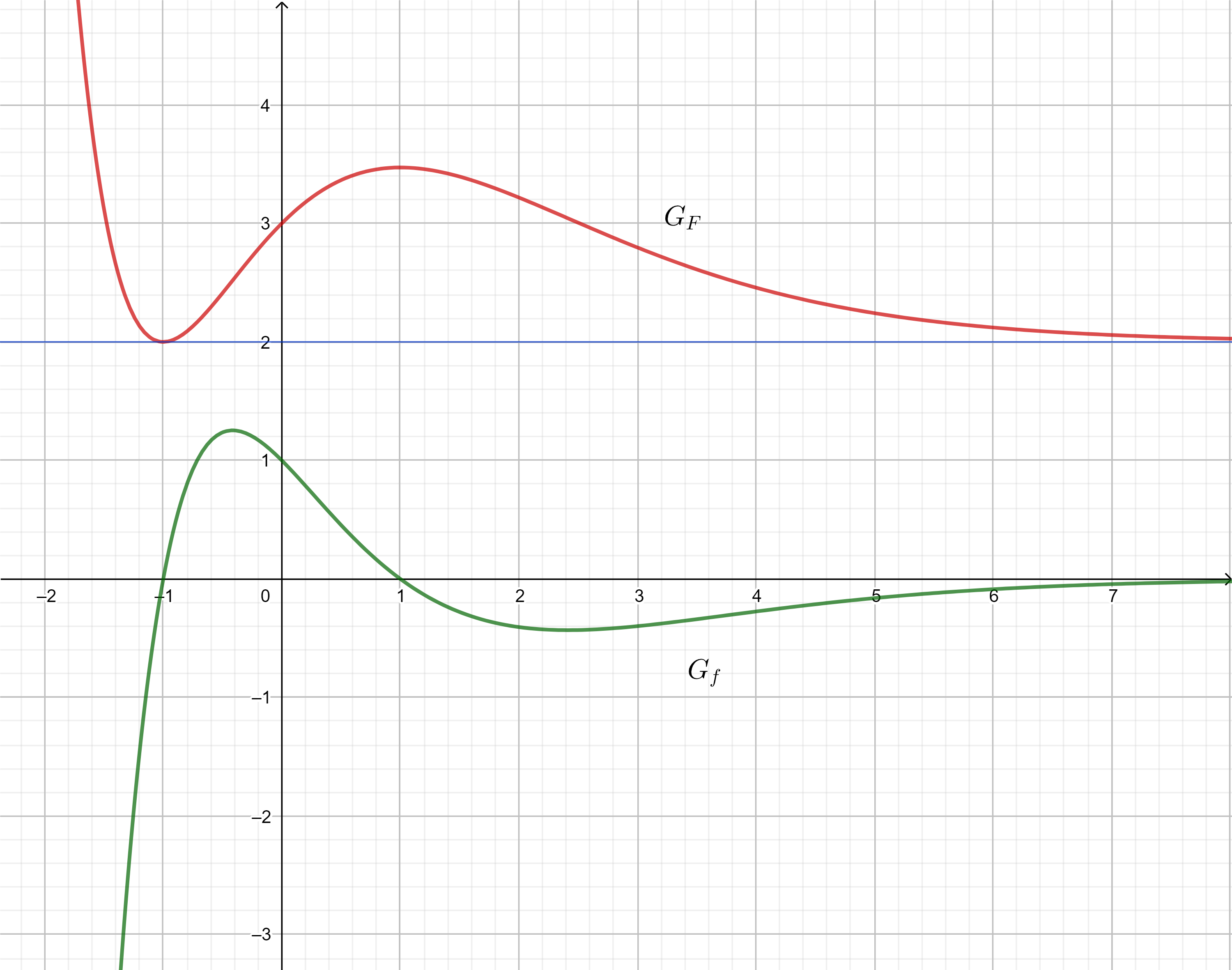
Gegeben ist die in definierte Funktion . Die Abbildung zeigt den Graphen von f.
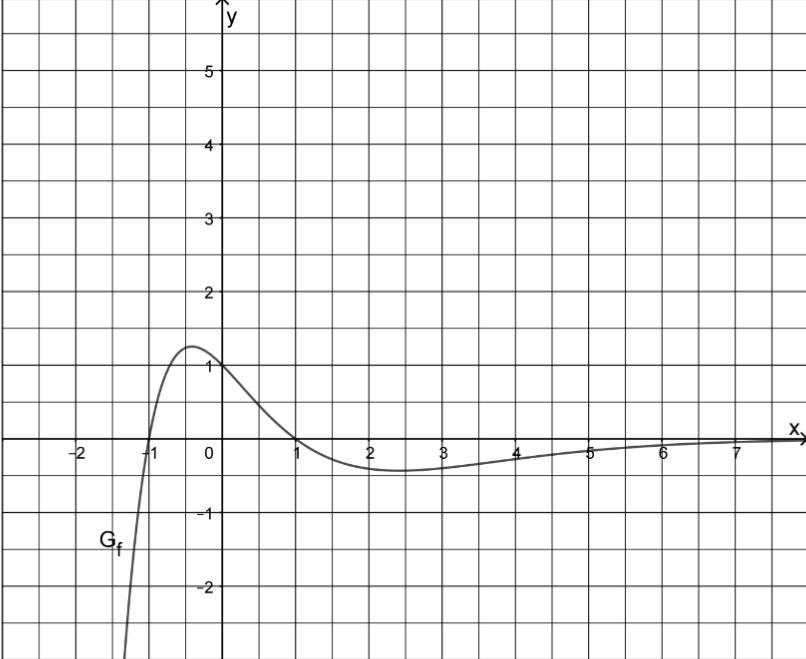
Zeigen Sie, dass genau zwei Nullstellen besitzt. (2P)
Bestimmen Sie rechnerisch die x-Koordinaten der beiden Extrempunkte von . (4P)
(zur Kontrolle: )
Ermitteln Sie anhand der Abbildung einen Näherungswert für das Integral . (4P)
Die in definierte Funktion ist diejenige Stammfunktion von , deren Graph durch den Punkt verläuft.
Begründen Sie mithilfe der Abbildung, dass der Graph von im Punkt einen Tiefpunkt besitzt. (2P)
Skizzieren Sie in der Abbildung den Graphen von . Berücksichtigen Sie dabei insbesondere, dass und gilt. (3P)
Deuten Sie die Aussage in Bezug auf geometrisch. (2P)
Betrachtet wird nun die Schar der in definierten Funktionen
mit . Der Graph von wird mit bezeichnet. Für ergibt sich die bisher betrachtete Funktion .
Geben Sie in Abhängigkeit von die Anzahl der Nullstellen von an. (2P)
Für einen bestimmten Wert von besitzt zwei Schnittpunkte mit der x-Achse, die voneinander den Abstand haben. Berechnen Sie diesen Wert. (3P)
Beurteilen Sie, ob es einen Wert von gibt, sodass und bezüglich der x-Achse symmetrisch zueinander liegen. (2P)
- 2
Betrachtet wird die in definierte Funktion . Ihr Graph wird mit bezeichnet.
Zeigen Sie, dass streng monoton zunehmend ist und die Wertemenge besitzt. (5P)
(zur Kontrolle: )
Geben Sie an und zeichnen Sie im Bereich unter Berücksichtigung der bisherigen Ergebnisse und der Tatsache, dass in seinen einzigen Wendepunkt hat, in ein Koordinatensystem ein. (3P)
Der Graph der Funktion geht aus durch Strecken und Verschieben hervor. Die Wertemenge von ist . Geben Sie einen möglichen Funktionsterm für an. (2P)
Es wird das Flächenstück zwischen und der x-Achse im Bereich mit betrachtet. Bestimmen Sie den Wert von so, dass die y-Achse dieses Flächenstück halbiert. (6P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?