Klammern ausmultiplizieren: Tabellenmethode

Tabellenmethode

Es gibt eine Möglichkeit, wie du dir beim Ausmultiplizieren von Klammern bessere Übersicht verschaffen kannst. Du legst eine Tabelle an, wie in der Abbildung dargestellt:

• In die erste Spalte der Tabelle trägst du die Glieder der ersten Klammer ein,

• in die erste Zeile der Tabelle trägst du die Glieder der zweiten Klammer ein.

 Achte dabei auf Minuszeichen. Wenn ein Minuszeichen vorkommt, betrachtest du es als Vorzeichen des jeweiligen Glieds.

Beispielsweise trägst du den Ausdruck $(3a + 2b)\cdot(5x - 8y)$ folgendermaßen in die Tabelle ein:

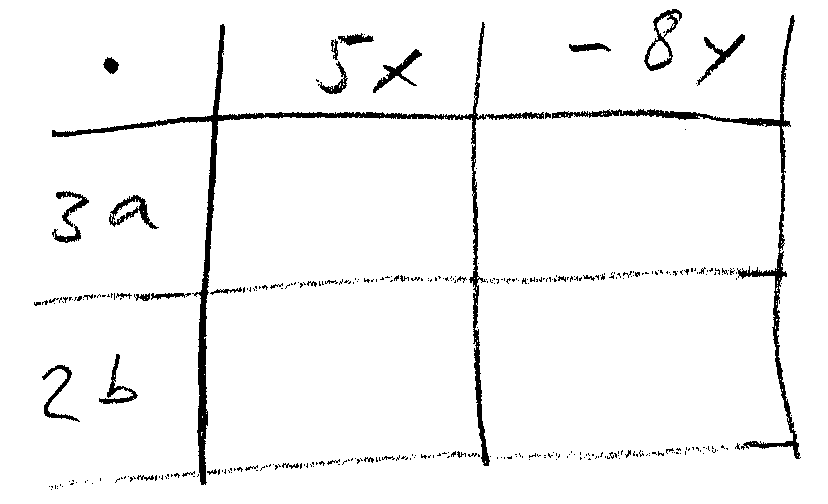
• Dann füllst du die Felder der Tabelle aus, indem du jeweils die Glieder, die in der ersten Spalte bzw. ersten Zeile des jeweiligen Feldes stehen, miteinander multiplizierst.

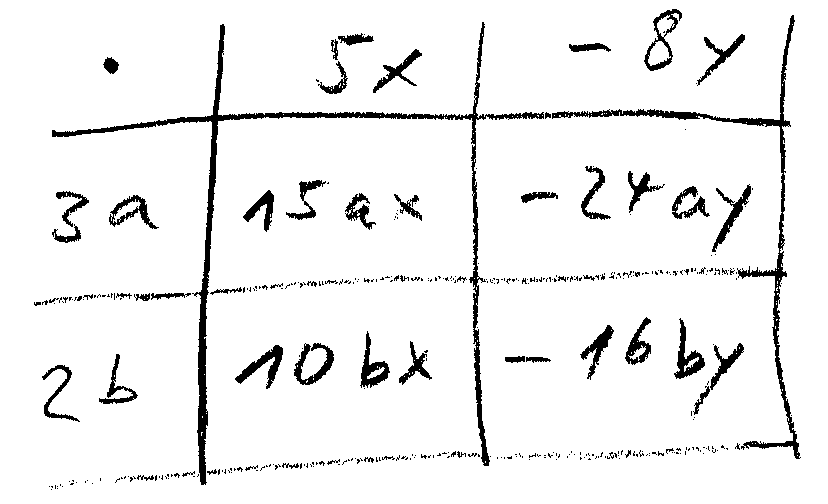
• Zum Schluss liest du die Einträge der inneren Felder der Tabelle aus und erhältst das Ergebnis:

Die Tabellenmethode stellt sicher, dass du wirklich jedes Glied der ersten Klammer mit jedem Glied der zweiten Klammer multiplizierst. Und du kannst noch einmal nachprüfen, ob du alles richtig multipliziert hast.

Ein weiteres Beispiel

Vielleicht findest du es sehr umständlich, extra eine Tabelle zu zeichnen. Aber du hast den Vorteil, dass du auch hinterher noch einmal mühelos überprüfen kannst, ob du alles richtig gerechnet hast – insbesondere bei Klammern mit mehr als zwei Gliedern und mit mehreren Minuszeichen:

Du gehst wieder genauso vor wie eben: Du legst eine Tabelle an und beschriftest die erste Spalte und die erste Zeile mit den jeweiligen Gliedern der Klammern. Achte dabei auf die Minuszeichen.

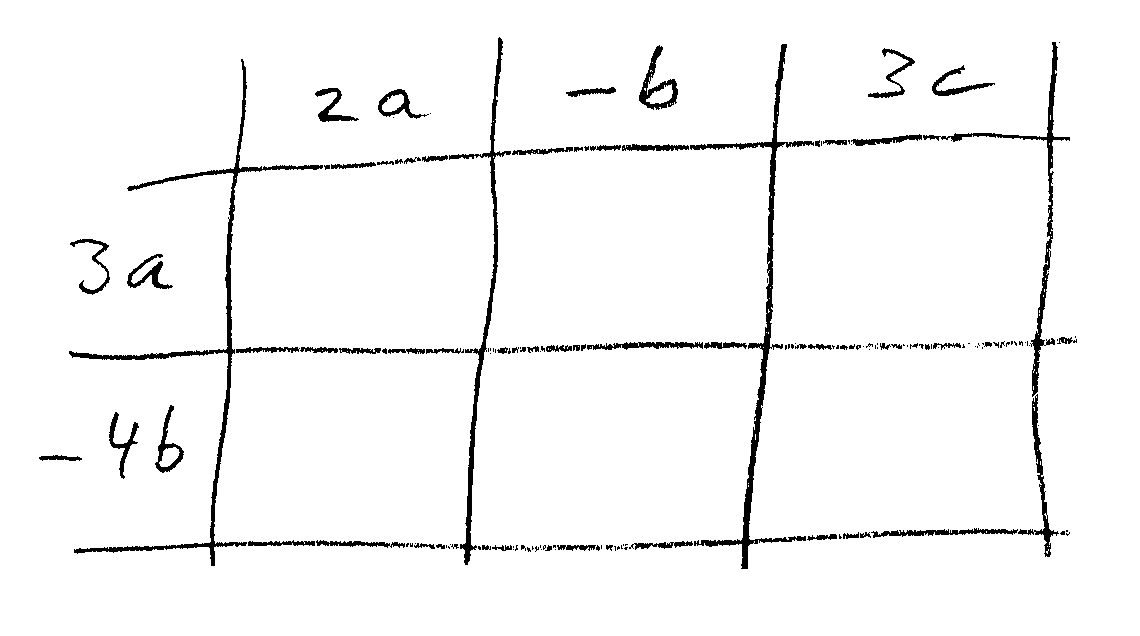
Dann füllst du die Felder der Tabelle aus, indem du die Glieder, die in der zugehörigen ersten Spalte und ersten Zeile stehen, miteinander multiplizierst:

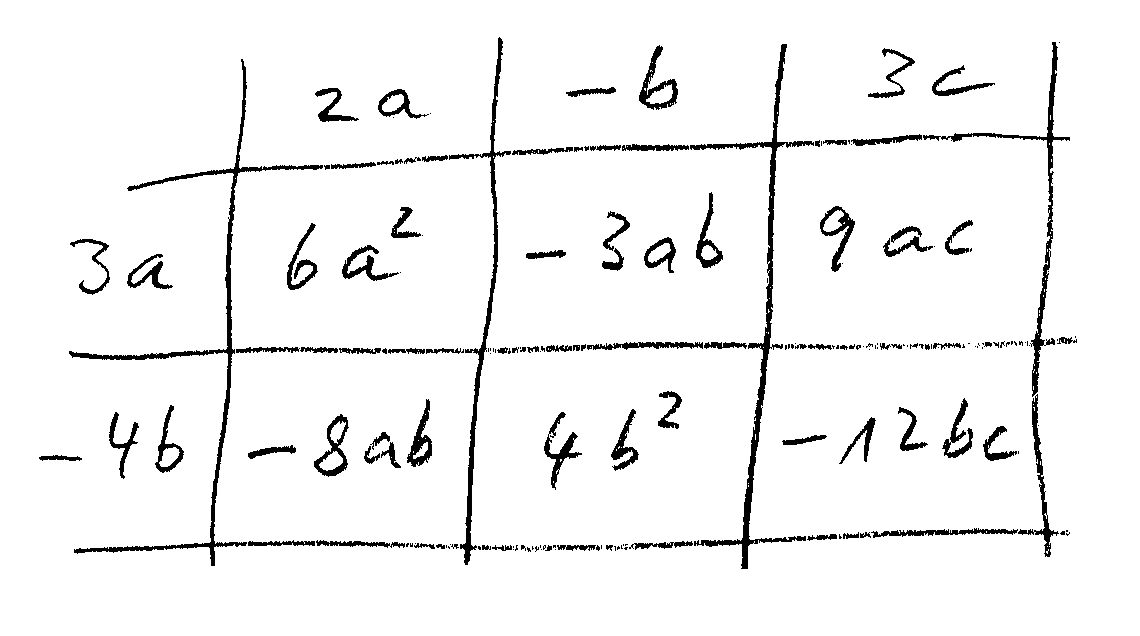
Dann liest du die Einträge in den inneren Feldern aus und erhältst das Ergebnis:

Anschließend kannst du noch $-3ab$ und $-8ab$ zu $-11ab$ zusammenfassen.

Nachkontrolle

Wenn du in der Mathearbeit noch Zeit hast, überprüfst du noch einmal alles.

Ohne die Tabellenmethode bleibt dir nichts anderes übrig, als dieselbe Aufgabe noch einmal zu rechnen – und dabei womöglich dieselben Fehler noch einmal zu machen.

Mit der Tabellenmethode kannst du sehr kleinteilig alle Rechenschritte noch einmal nachprüfen:

• Hast du die Glieder der Klammern richtig aus der Aufgabe in die erste Spalte und die erste Zeile der Tabelle übertragen?

• Hast du dabei alle Minuszeichen berücksichtigt?

• Hast du alle Einträge der inneren Felder richtig ausgerechnet?

• Stimmen alle Vorzeichen in den inneren Feldern?

• Hast du die Einträge der inneren Felder zum Schluss vollständig und korrekt ausgelesen?

Vorzeichencheck

Wenn in der ersten Spalte ein Glied mit einem Minuszeichen steht, hier zum Beispiel $-4b$, dann entsteht eine negative Zeile: Alle Einträge in der Zeile sind negativ – außer dort, wo eine negative Spalte kreuzt (hier beim Eintrag $4b^2$).

Umgekehrt genauso: Wenn in der ersten Zeile ein Glied mit einem Minuszeichen steht, hier zum Beispiel $-b$, dann entsteht eine negative Spalte: Alle Einträge in der Spalte sind negativ – außer dort, wo eine negative Zeile kreuzt (hier beim Eintrag $4b^2$).

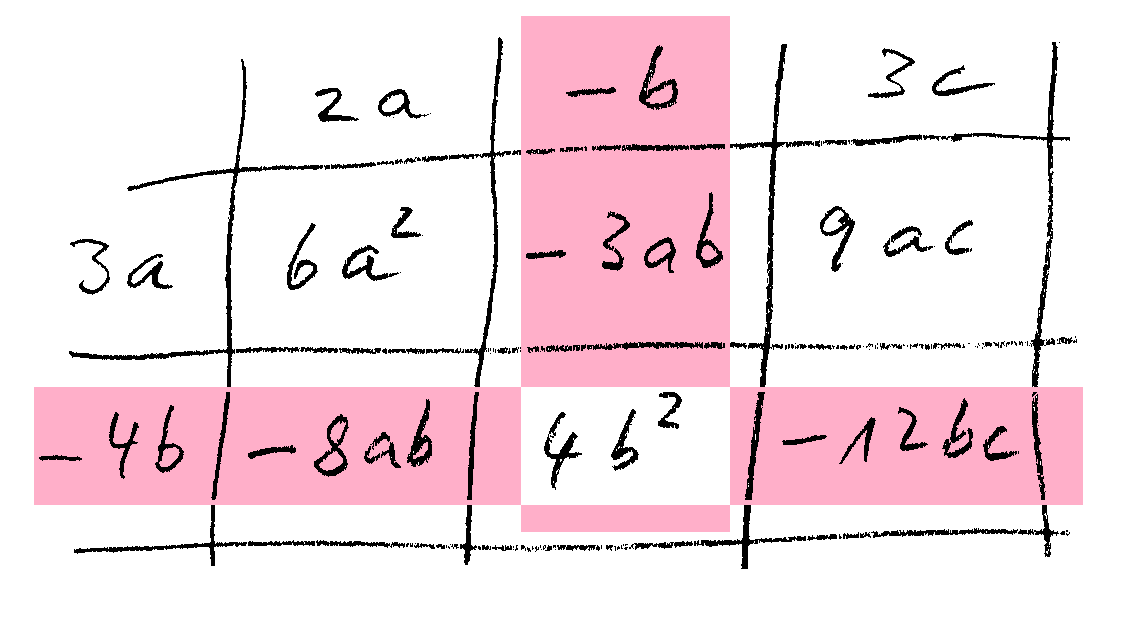
Nobody is perfect - jeder macht einmal Fehler. Vielleicht bist du kurz abgelenkt, weil deinem Sitznachbarn das Radiergummi heruntergefallen ist und in der Klasse herumhüpft - und schon ist es passiert: Du hast ein Minuszeichen vergessen.

Umso wichtiger ist es, wenn du eine einfache Möglichkeit hast, alles noch einmal nachzukontrollieren, wie hier mit der Tabellenmethode.

Probiere einmal aus, ob dir die Tabellenmethode gefällt, indem du ein paar Aufgaben rechnest.