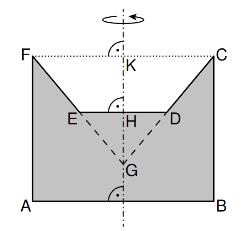
Aufgabe A3
Die Skizze zeigt den Axialschnitt eines Körpers mit der Rotationsachse . Der Punkt ist der Schnittpunkt der Geraden und .
Es gilt: ; ; ; ;
.
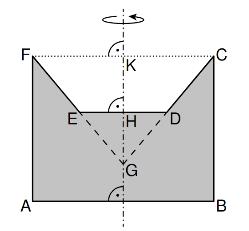
Berechnen Sie das Volumen des Rotationskörpers auf zwei Stellen nach dem Komma gerundet. (5 P)
Zwischenergebnisse: ;