Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A1
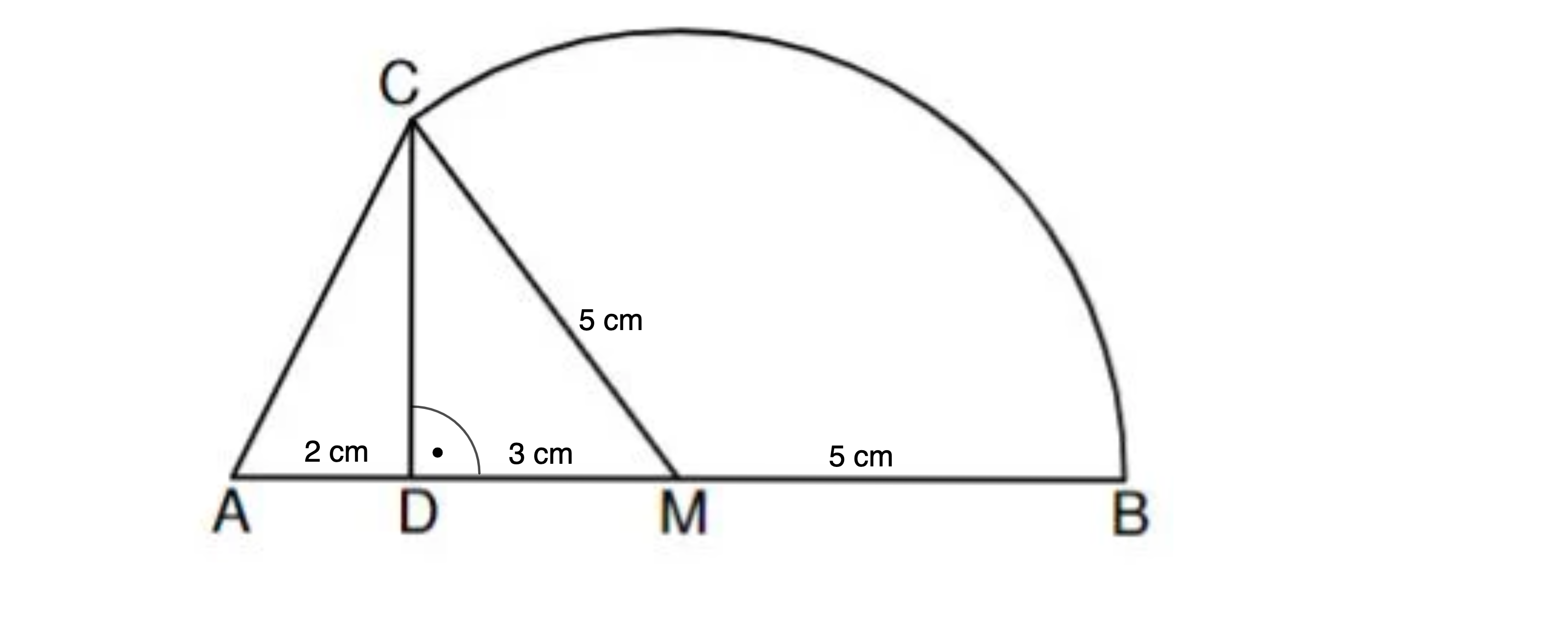
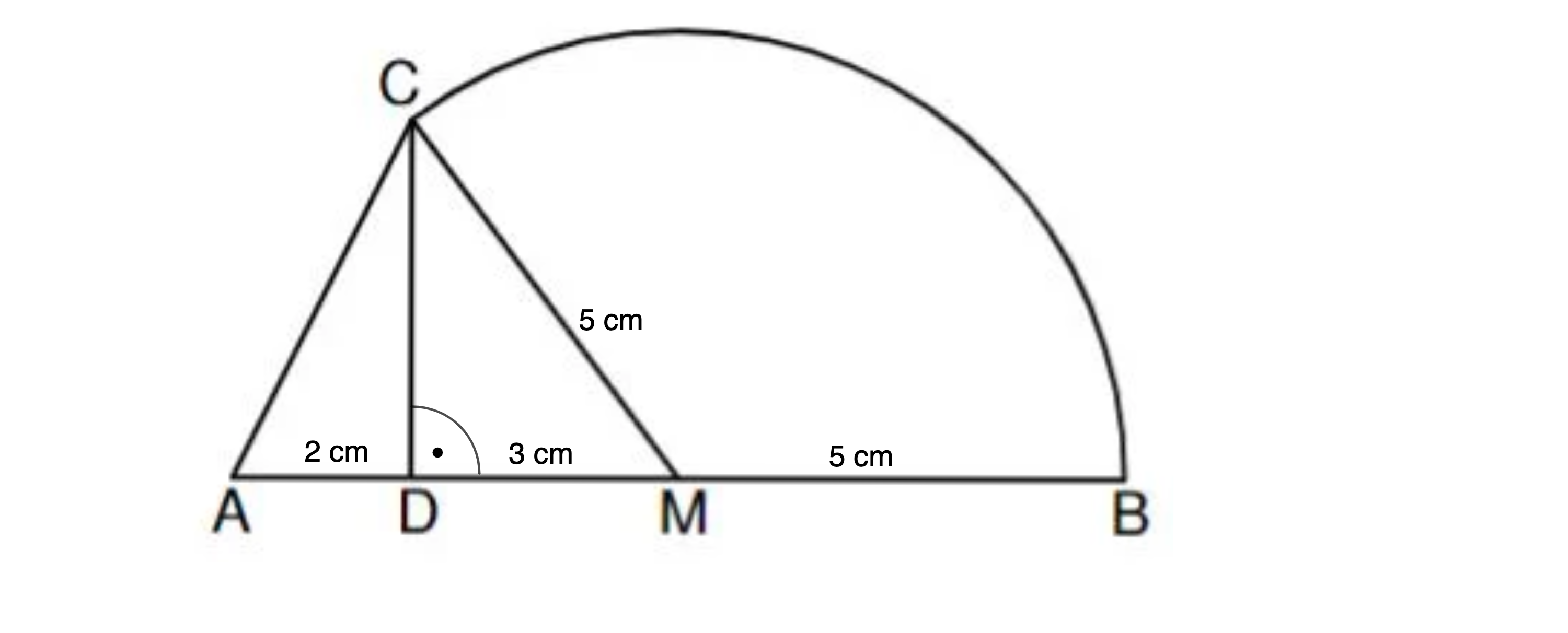
Die Skizze zeigt die Figur, die durch die Strecken $[A B]$ und $[A C]$ sowie den Kreisbogen $\overset{⌢}{B}$ mit dem Mittelpunkt $M$ und dem Radius $r = M B$ begrenzt wird.
Es gilt: $A D = 2$ cm; $M A = M B = M C = 5$ cm; $∢ M D C = 90 °$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
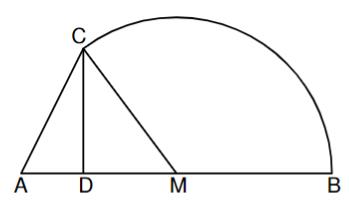
1. Berechnen Sie das Maß des Winkels $C M D$ und die Länge $b$ des Kreisbogens $\overset{⌢}{B}$ . (3 P)
  $[$ Teilergebnis: $∢ C M D = 53,13 °$ $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt zusammengesetzter Figuren
  Berechnung des Winkels
  Berechne das Maß des Winkels $C M D$ und die Länge $b$ des Kreisbogens $\overset{⌢}{B} .$
  Berechne den Kosinus des Winkels $C M D$ .
  $\cos ∢ C M D = \frac{3}{5} = 0,6 \Rightarrow ∢ C M D = 53,13 °$
  Länge des Kreisbogens
  Berechne jetzt die Länge $b$ des Kreisbogens $\overset{⌢}{B} .$ Damit Du den Kreisbogen $\overset{⌢}{B}$ berechnen kannst, musst Du zuerst den Winkel $B M C$ berechnen.
  
  $∢ B M C = 180^{\circ} - {53,13}^{\circ} = {126,87}^{\circ}$
  
  $b = 2 r \cdot π \cdot \frac{∢ B M C}{360^{\circ}} \Rightarrow b = 2 \cdot 5 \cdot π \cdot \frac{{126,87}^{\circ}}{360^{\circ}} cm$
  Also ist $b = 11,07 cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne das Maß des Winkels $C M D$ . Verwende dazu die geeignete Winkelfunktion (Sinus, Kosinus, Tangens).
  Bestimme die Länge des Kreisbogens $\overset{⌢}{B}$ mithilfe des Winkels.
2. Ermitteln Sie rechnerisch den Flächeninhalt der Figur aus der Aufgabenstellung. (2 P)
  cm²
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecke, Vierecke, Kreise und andere ebene Figuren
  Flächeninhalt Dreieck $_{A M C}$
  Mit der allgemeinen Formel für den Flächeninhalt im Dreieck gilt:
  $A_{A M C} = \frac{1}{2} \cdot A M \cdot M C \cdot \sin ∢ C M D$ $∢ C M D = 53,13 °$
  $A_{A M C} = \frac{1}{2} \cdot 5 cm \cdot 5 cm \cdot \sin 53,13 ° \Rightarrow A_{A M C} = \frac{1}{2} \cdot 25 \cdot 0,7999 {cm}^{2}$
  $A_{A M C} = 10 {cm}^{2}$
  Flächeninhalt Kreissektor $_{M B C}$
  Die Fläche des Kreissektors ergibt sich mithilfe des Winkels zu:
  $A_{M B C} = {M B}^{2} \cdot π \cdot \frac{∢ C M B}{360^{\circ}} \Rightarrow A_{M B C} = (5 cm)^{2} \cdot π \cdot \frac{{126,87}^{\circ}}{360^{\circ}}$
  $A_{M B C} = 27,68 {cm}^{2}$
  Gesamtfläche
  $A_{F i g u r} = A_{A M C} + A_{M B C} \Rightarrow A_{F i g u r} = 10 {cm}^{2} + 27,68 {cm}^{2}$
  $A_{F i g u r} = 37,68 {cm}^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Figur setzt sich zusammen aus einem Dreieck und einem Kreissektor.
  Berechne den Flächeninhalt des Dreiecks und den Flächeninhalt des Kreissektors und addiere die Werte.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A2
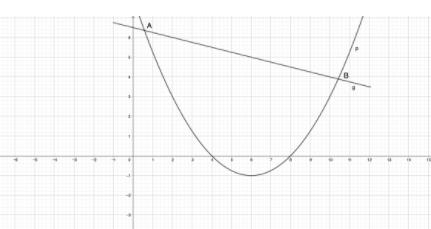
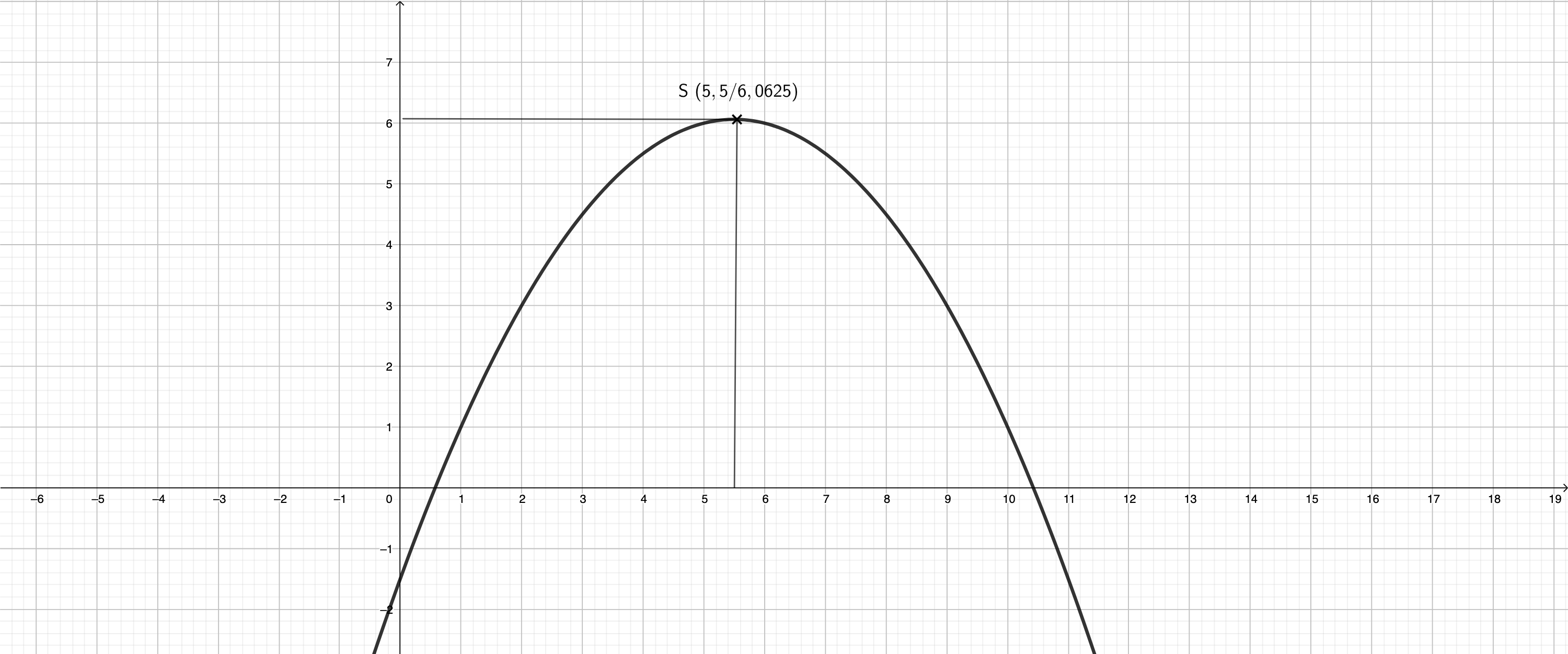
Gegeben sind die Parabel $p$ mit der Gleichung $y = 0,25 x^{2} - 3 x + 8$ und die Gerade $g$ mit der Gleichung $y = - 0,25 x + 6,5$ . Es gilt: $𝔾 = ℝ$ x $ℝ$ .
Die Punkte $A$ und $B$ sind die Schnittpunkte der Parabel $p$ und der Gerade $g$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
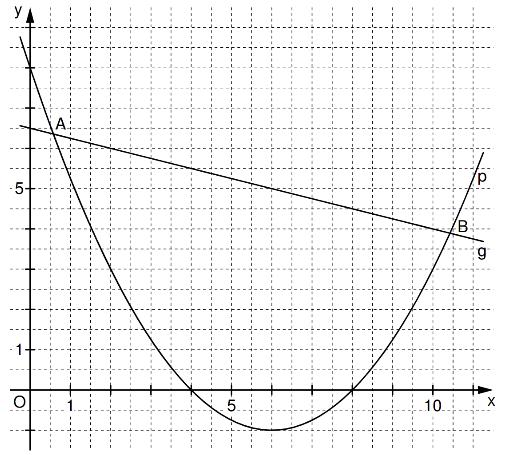
1. Berechnen Sie die Koordinaten der Punkte $A$ und $B$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
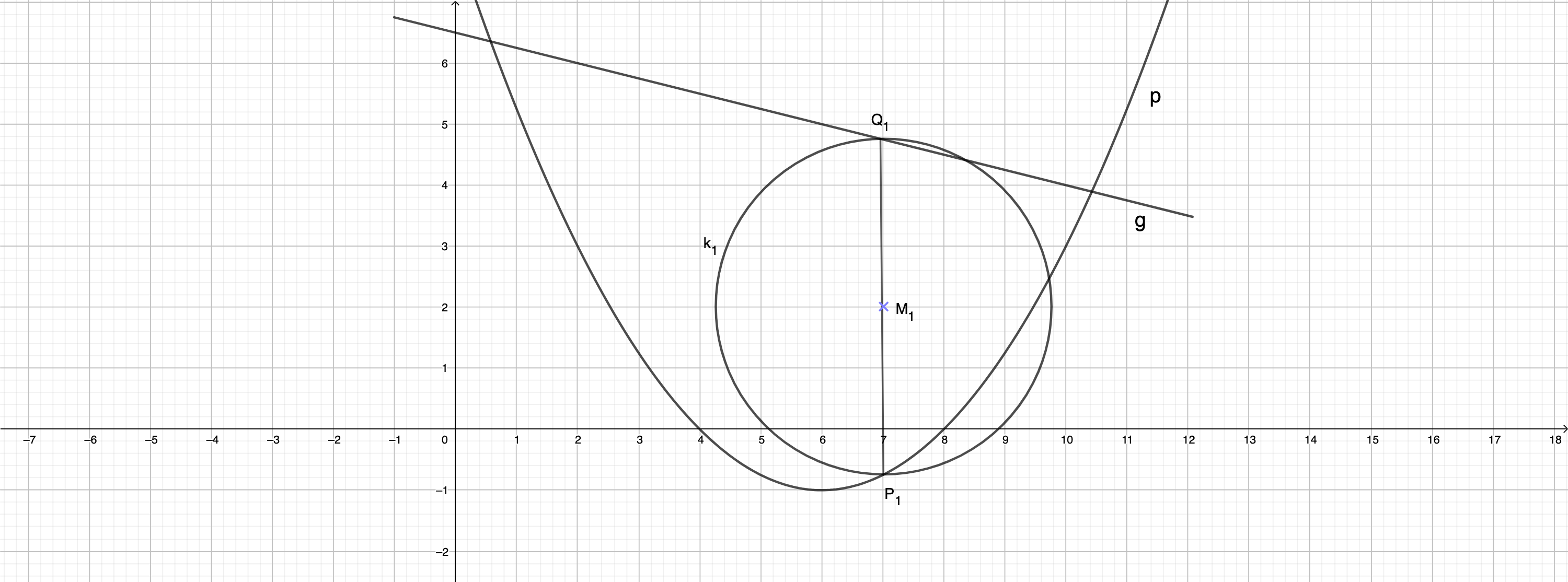
  Skizze
  Funktionsterme gleichsetzen
  $0,25 x^{2} - 3 x + 8 = - 0,25 x + 6,5$
  Fasse zusammen.
  $0,25 x^{2} - 2,75 x + 1,5 = 0$
  Quadratische Gleichung lösen
  Mit der abc-Formel ist die Lösung der Gleichung für $a = 0,25, b = - 2,75, c = 1,5 :$
  $x_{1,2} = \frac{2,75 \pm \sqrt{(- 2,75)^{2} - 4 \cdot (0,25) \cdot (1,5)}}{0,25 \cdot 2}$
  $x_{1} = 0,58; x_{2} = 10,42$
  $L = {0,58; 10,42}$
  Funktionswerte berechnen und Koordinaten angeben
  $A (0,58 | - 0,25 \cdot 0,58 + 6,5) \Rightarrow A (0,58 ∣ 6,36)$
  $B (10,42 | (- 0,25 \cdot 10,42 + 6,5) \Rightarrow B (10,42 ∣ 3,90)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze die Funktionsterme gleich $p = g $ .
  Bestimme die Lösungen $x_{1}, x_{2}$ .
  Berechne die Funktionswerte für $x_{1}, x_{2}$ , um die Koordinaten von $A$ und $B$ angeben zu können.
2. Punkte $P_{n} (x | 0,25 x^{2} - 3 x + 8)$ auf $p$ und Punkte $Q_{n} (x | - 0,25 x + 6,5)$ auf $g$ haben dieselbe Abszisse $x$ . Für die Strecken $[P_{n} Q_{n}]$ gilt: $y_{Q_{n}} > y_{P_{n}}$ . Die Mittelpunkte $M_{n}$ der Strecken $[P_{n} Q_{n}]$ sind zugleich Mittelpunkte von Kreisen $k_{n}$ mit den Durchmessern $P_{n} Q_{n} .$
  Zeichnen Sie die Strecke $[P_{1} Q_{1}]$ sowie den Mittelpunkt $M_{1}$ und den Kreis $k_{1}$ mit dem Durchmesser $P_{1} Q_{1}$ für $x = 7$ in das Koordinatensystem zur Aufgabenstellung ein. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Einzeichnen der Punkte und Strecken
  Die Punkte $Q_{n}$ liegen auf der Gerade $g$ , die Punkte $P_{n}$ auf der Parabel.
  Beide liegen übereinander, mit verschiedenen Funktionswerten:
  Skizze
  Der Mittelpunkt ergibt sich aus dem Mittel der Funktionswerte:
  $M (7 | \frac{y_{Q_{1}} - y_{P_{1}}}{2}) = M (7 | \frac{4,75 - (- 0,75)}{2}) = M (7 | 2,75)$
  Mit dem Zirkel kann der Kreis mit dem Mittelpunkt $M$ und dem passenden Radius konstruiert werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zeichne die Strecke $[P_{1} Q_{1}]$ sowie den Punkt $M_{1}$ und den Kreis $k_{1}$ in das Koordinatensystem ein.
3. Zeigen Sie rechnerisch, dass für die Länge der Strecken $[P_{n} Q_{n}]$ in Abhängigkeit von der Abszisse $x$ der Punkte $P_{n}$ gilt: (1 P)
  $P_{n} Q_{n} (x) = (- 0,25 x^{2} + 2,75 x - 1,5) cm$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
  Länge der Strecke
  $P_{n} Q_{n} (x) = \underset{Differenz der y-Werte}{\underset{⏟}{[y_{Q_{n}} - y_{P_{n}}]}} = [- 0,25 x + 6,5 - (0,25 x^{2} - 3 x + 8)] LE$
  $P_{n} Q_{n} (x) = (- 0,25 x + 6,5 - 0,25 x^{2} + 3 x - 8) LE$
  $P_{n} Q_{n} (x) = (- 0,25 x^{2} + 2,75 x - 1,5) LE$
  $x \in ℝ; x \in] 0,58; 10,42 [$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Differenz aus den y-Werten der beiden Punkte.
4. Unter den Kreisen $k_{n}$ gibt es einen Kreis $k_{0}$ mit maximalem Umfang $u_{m a x}$ .
  Berechnen Sie $u_{m a x}$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktion
  Maximum der Strecke $P_{n} Q_{n} (x)$
  Unter den Kreisen $k_{n}$ gibt es einen Kreis $k_{0}$ mit maximalem Umfang $u_{m a x}$ . Berechne $u_{m a x}$ .
  $u (x) = d \cdot π = (P_{n} Q_{n} (x) \cdot π) LE$
  $u (x) = [(- 0,25 x^{2} + 2,75 x - 1,5) \cdot π] LE$
  Skizze der Parabel
  Da es sich hier um eine nach unten geöffnete Parabel handelt, liegt der maximale Funktionswert im Scheitel der Parabel. Mit der Scheitelpunktform kannst Du den Scheitelpunkt $y_{s}$ berechnen.
  Scheitel der Parabel bestimmen
  Wandle die Funktion $u (x)$ in die Scheitelpunktform um.
  $u (x) = (- 0,25 x^{2} + 2,75 x - 1,5) \cdot π LE$
  $u (x) = - 0,25 (x^{2} - 11 x + 6) \cdot π LE$
  $u (x) = - 0,25 [(x - 5,5)^{2} - {5,5}^{2} + 6] \cdot π LE$
  $u (x) = - 0,25 [(x - 5,5)^{2} - 30,25 + 6] \cdot π LE$
  $u (x) = - 0,25 [(x - 5,5)^{2} - 24,25] \cdot π LE$
  $u (x) = [- 0,25 (x - 5,5)^{2} + 6,0625] \cdot π LE \Rightarrow U_{m a x} = 6,0625 \cdot π LE$
  $u_{m a x} \approx 19,05 LE$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme, für welchen Wert von $x$ die Länge der Strecke $P_{n} Q_{n} (x)$ maximal ist.
  Bestimme dazu den Scheitel der Parabel
  $P_{n} Q_{n} (x) = (- 0,25 x^{2} + 2,75 x - 1,5) LE$
  (aus Teilaufgabe (c)).
  $P_{n} Q_{n} (x)$ ist der Durchmesser der Kreise. Wenn dieser Wert maximal ist, dann auch die Fläche der Kreise.
5. Ein Kreis $k_{3}$ hat den 4-fachen Durchmesser eines Kreises $k_{2}$ . Hat $k_{3}$ dann den 16-fachen Flächeninhalt von $k_{2}$ ?
  Begründen Sie Ihre Antwort. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Begründung
  Ein Kreis $k_{3}$ hat den $4$ -fachen Durchmesser eines Kreises $k_{2}$ . Hat $k_{3}$ dann den $16$ -fachen Flächeninhalt von $k_{2}$ ? Begründe Deine Antwort.
  $k_{3}$ hat den 16-fachen Flächeninhalt von $k_{2}$ , denn es gilt:
  Aus $d_{3} = 4 \cdot d_{2}$ folgt: $r_{3} = 4 \cdot r_{2}$ .
  Somit gilt: $A_{3} = r_{3}^{2} \cdot π = (4 \cdot r_{2})^{2} \cdot π = 16 \cdot r_{2}^{2} \cdot π = 16 \cdot A_{2}$ .
  Ja, $k_{3}$ hat dann den 16-fachen Flächeninhalt von $k_{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Begründe die Behauptung mit der Formel für die Kreisfläche $A = π \cdot r^{2}$ .
  Untersuche, was passiert, wenn der Radius vervierfacht wird (und anschließend quadriert wird).
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A3
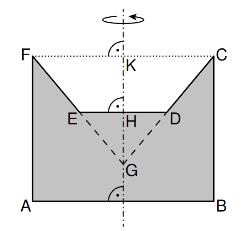
Die Skizze zeigt den Axialschnitt $A B C D E F$ eines Körpers mit der Rotationsachse $G$ $K$ . Der Punkt $G$ ist der Schnittpunkt der Geraden $C D$ und $F E$ .
Es gilt: $A B = C F = 5 cm$ ; $A F = B C = 4 cm$ ; $E D = 2,4 cm$ ; $∢ G F K = 50 °$ ;
$[A F] ‖ [G K] ‖ [B C]$ .
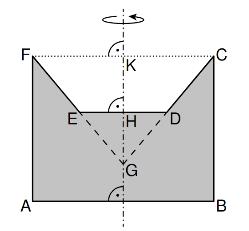
Berechnen Sie das Volumen des Rotationskörpers auf zwei Stellen nach dem Komma gerundet. (5 P)
$[$ Zwischenergebnisse: $G K = 2,98 cm$ ; $G H = 1,43 cm$ $]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
Volumen des gesamten Körpers
Die Skizze zeigt den Axialschnitt $A B C D E F$ eines Körpers mit der Rotationsachse $G$ $K$ . Der Punkt $G$ ist der Schnittpunkt der Geraden $C D$ und $F E$ .
Es gilt: $A B = C F = 5 cm$ ; $A F = B C = 4 cm$ ; $E D = 2,4 cm$ ; $∢ G F K = 50 °$ ;
$[A F] ‖ [G K] ‖ [B C]$ .
Skizze des Körpers
Das Volumen des Gesamtkörpers (Zylinder) ist: $V = {F K}^{2} \cdot π \cdot A F = 78,54 {cm}^{3}$
Volumen des Kegels
Berechne die Länge der Strecke $G K$ :
$\frac{G K}{F K} = \tan ∢ G F K \Rightarrow G K = 2,5 cm \cdot \tan 50^{\circ}$
$G K = 2,5 cm \cdot 1,1918$
$G K = 2,98 c m$
Damit ist das Volumen des Kegels: $V = \frac{1}{3} \cdot {F K}^{2} \cdot π \cdot G K = 19,50 {cm}^{3}$
Volumen der Kegelspitze
Berechne die Länge der Strecke $G H$ .
$\frac{G H}{G K} = \frac{E D}{F C}$
$G H = \frac{2,98 cm \cdot 2,40 cm}{5 cm}$
$G H = 1,43 cm$
Damit ist das Volumen der Kegelspitze: $V = \frac{1}{3} \cdot {E H}^{2} \cdot π \cdot G H = 2,16 {cm}^{3}$
Gesamtvolumen
Berechne das Volumen des Rotationskörpers.
$V = {F K}^{2} \cdot π \cdot A F - \frac{1}{3} \cdot {F K}^{2} \cdot π \cdot G K + \frac{1}{3} \cdot {E H}^{2} \cdot π \cdot G H$
$V = [(5 \cdot 0,5)^{2} \cdot π \cdot 4 - \frac{1}{3} \cdot (5 \cdot 0,5)^{2} \cdot π \cdot 2,98 + \frac{1}{3} \cdot (0,5 \cdot 2,4)^{2} \cdot π \cdot 1,43] {cm}^{3}$
$V = 61,19 {cm}^{3}$
Berechne zunächst das Volumen des gesamten Körpers.
Ziehe dann das Volumen des Kegels ab und addiere anschließend das Volumen der Kegelspitze.