Teil A - lernen mit Serlo!

Aufgabe A2

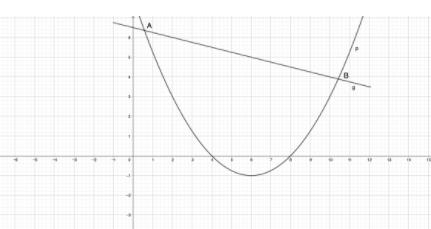
Gegeben sind die Parabel $p$ mit der Gleichung $y = 0,25 x^{2} - 3 x + 8$ und die Gerade $g$ mit der Gleichung $y = - 0,25 x + 6,5$ . Es gilt: $𝔾 = ℝ$ x $ℝ$ .

Die Punkte $A$ und $B$ sind die Schnittpunkte der Parabel $p$ und der Gerade $g$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

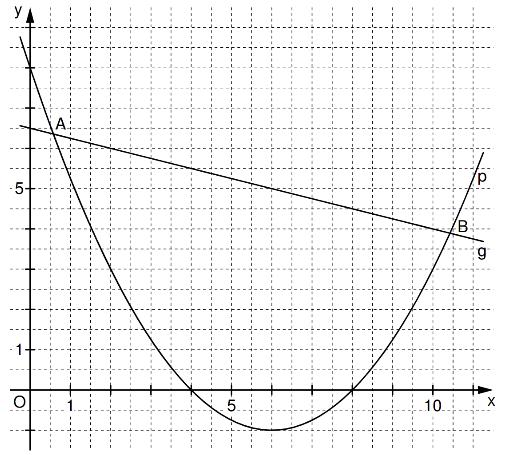
Berechnen Sie die Koordinaten der Punkte $A$ und $B$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
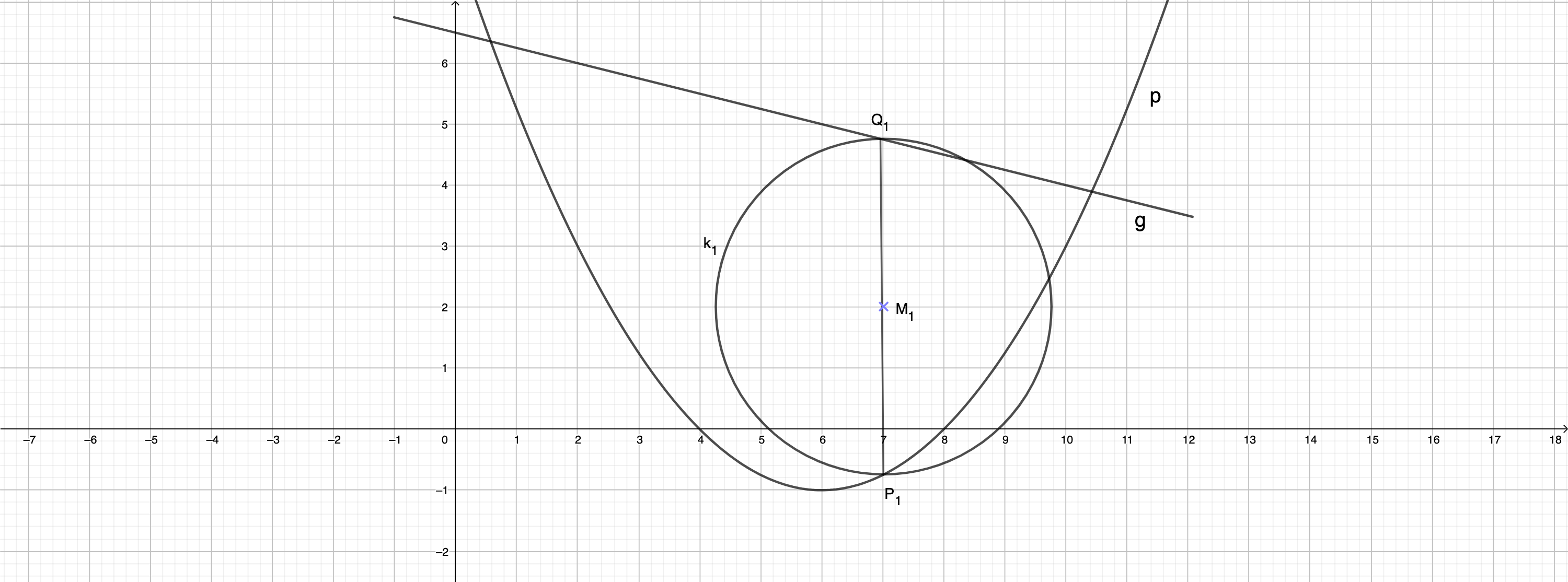
Skizze
Funktionsterme gleichsetzen
$0,25 x^{2} - 3 x + 8 = - 0,25 x + 6,5$
Fasse zusammen.
$0,25 x^{2} - 2,75 x + 1,5 = 0$
Quadratische Gleichung lösen
Mit der abc-Formel ist die Lösung der Gleichung für $a = 0,25, b = - 2,75, c = 1,5 :$
$x_{1,2} = \frac{2,75 \pm \sqrt{(- 2,75)^{2} - 4 \cdot (0,25) \cdot (1,5)}}{0,25 \cdot 2}$
$x_{1} = 0,58; x_{2} = 10,42$
$L = {0,58; 10,42}$
Funktionswerte berechnen und Koordinaten angeben
$A (0,58 | - 0,25 \cdot 0,58 + 6,5) \Rightarrow A (0,58 ∣ 6,36)$
$B (10,42 | (- 0,25 \cdot 10,42 + 6,5) \Rightarrow B (10,42 ∣ 3,90)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze die Funktionsterme gleich $p = g $ .
Bestimme die Lösungen $x_{1}, x_{2}$ .
Berechne die Funktionswerte für $x_{1}, x_{2}$ , um die Koordinaten von $A$ und $B$ angeben zu können.
Punkte $P_{n} (x | 0,25 x^{2} - 3 x + 8)$ auf $p$ und Punkte $Q_{n} (x | - 0,25 x + 6,5)$ auf $g$ haben dieselbe Abszisse $x$ . Für die Strecken $[P_{n} Q_{n}]$ gilt: $y_{Q_{n}} > y_{P_{n}}$ . Die Mittelpunkte $M_{n}$ der Strecken $[P_{n} Q_{n}]$ sind zugleich Mittelpunkte von Kreisen $k_{n}$ mit den Durchmessern $P_{n} Q_{n} .$
Zeichnen Sie die Strecke $[P_{1} Q_{1}]$ sowie den Mittelpunkt $M_{1}$ und den Kreis $k_{1}$ mit dem Durchmesser $P_{1} Q_{1}$ für $x = 7$ in das Koordinatensystem zur Aufgabenstellung ein. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
Einzeichnen der Punkte und Strecken
Die Punkte $Q_{n}$ liegen auf der Gerade $g$ , die Punkte $P_{n}$ auf der Parabel.
Beide liegen übereinander, mit verschiedenen Funktionswerten:
Skizze
Der Mittelpunkt ergibt sich aus dem Mittel der Funktionswerte:
$M (7 | \frac{y_{Q_{1}} - y_{P_{1}}}{2}) = M (7 | \frac{4,75 - (- 0,75)}{2}) = M (7 | 2,75)$
Mit dem Zirkel kann der Kreis mit dem Mittelpunkt $M$ und dem passenden Radius konstruiert werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeichne die Strecke $[P_{1} Q_{1}]$ sowie den Punkt $M_{1}$ und den Kreis $k_{1}$ in das Koordinatensystem ein.
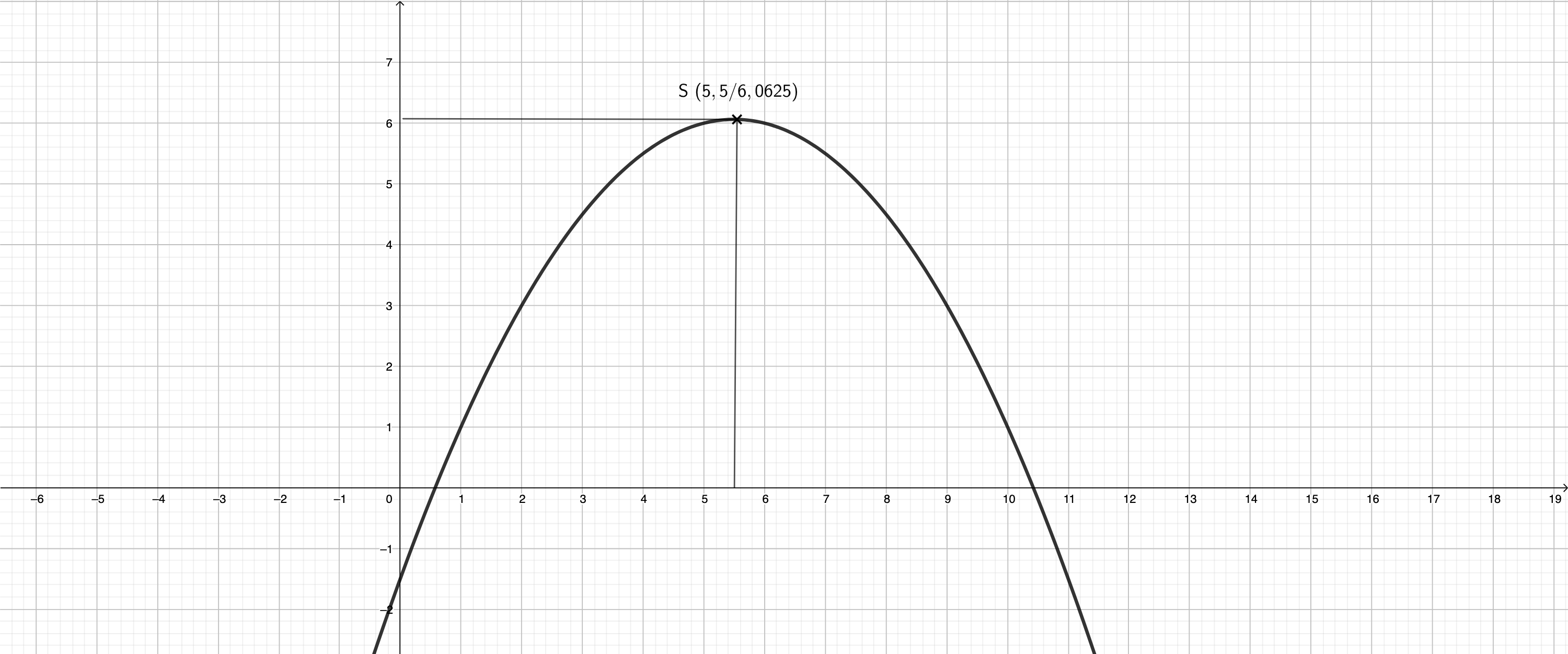
Zeigen Sie rechnerisch, dass für die Länge der Strecken $[P_{n} Q_{n}]$ in Abhängigkeit von der Abszisse $x$ der Punkte $P_{n}$ gilt: (1 P)
$P_{n} Q_{n} (x) = (- 0,25 x^{2} + 2,75 x - 1,5) cm$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Länge der Strecke
$P_{n} Q_{n} (x) = \underset{Differenz der y-Werte}{\underset{⏟}{[y_{Q_{n}} - y_{P_{n}}]}} = [- 0,25 x + 6,5 - (0,25 x^{2} - 3 x + 8)] LE$
$P_{n} Q_{n} (x) = (- 0,25 x + 6,5 - 0,25 x^{2} + 3 x - 8) LE$
$P_{n} Q_{n} (x) = (- 0,25 x^{2} + 2,75 x - 1,5) LE$
$x \in ℝ; x \in] 0,58; 10,42 [$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Differenz aus den y-Werten der beiden Punkte.
Unter den Kreisen $k_{n}$ gibt es einen Kreis $k_{0}$ mit maximalem Umfang $u_{m a x}$ .
Berechnen Sie $u_{m a x}$ . (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktion
Maximum der Strecke $P_{n} Q_{n} (x)$
Unter den Kreisen $k_{n}$ gibt es einen Kreis $k_{0}$ mit maximalem Umfang $u_{m a x}$ . Berechne $u_{m a x}$ .
$u (x) = d \cdot π = (P_{n} Q_{n} (x) \cdot π) LE$
$u (x) = [(- 0,25 x^{2} + 2,75 x - 1,5) \cdot π] LE$
Skizze der Parabel
Da es sich hier um eine nach unten geöffnete Parabel handelt, liegt der maximale Funktionswert im Scheitel der Parabel. Mit der Scheitelpunktform kannst Du den Scheitelpunkt $y_{s}$ berechnen.
Scheitel der Parabel bestimmen
Wandle die Funktion $u (x)$ in die Scheitelpunktform um.
$u (x) = (- 0,25 x^{2} + 2,75 x - 1,5) \cdot π LE$
$u (x) = - 0,25 (x^{2} - 11 x + 6) \cdot π LE$
$u (x) = - 0,25 [(x - 5,5)^{2} - {5,5}^{2} + 6] \cdot π LE$
$u (x) = - 0,25 [(x - 5,5)^{2} - 30,25 + 6] \cdot π LE$
$u (x) = - 0,25 [(x - 5,5)^{2} - 24,25] \cdot π LE$
$u (x) = [- 0,25 (x - 5,5)^{2} + 6,0625] \cdot π LE \Rightarrow U_{m a x} = 6,0625 \cdot π LE$
$u_{m a x} \approx 19,05 LE$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme, für welchen Wert von $x$ die Länge der Strecke $P_{n} Q_{n} (x)$ maximal ist.
Bestimme dazu den Scheitel der Parabel
$P_{n} Q_{n} (x) = (- 0,25 x^{2} + 2,75 x - 1,5) LE$
(aus Teilaufgabe (c)).
$P_{n} Q_{n} (x)$ ist der Durchmesser der Kreise. Wenn dieser Wert maximal ist, dann auch die Fläche der Kreise.
Ein Kreis $k_{3}$ hat den 4-fachen Durchmesser eines Kreises $k_{2}$ . Hat $k_{3}$ dann den 16-fachen Flächeninhalt von $k_{2}$ ?
Begründen Sie Ihre Antwort. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
Begründung
Ein Kreis $k_{3}$ hat den $4$ -fachen Durchmesser eines Kreises $k_{2}$ . Hat $k_{3}$ dann den $16$ -fachen Flächeninhalt von $k_{2}$ ? Begründe Deine Antwort.
$k_{3}$ hat den 16-fachen Flächeninhalt von $k_{2}$ , denn es gilt:
Aus $d_{3} = 4 \cdot d_{2}$ folgt: $r_{3} = 4 \cdot r_{2}$ .
Somit gilt: $A_{3} = r_{3}^{2} \cdot π = (4 \cdot r_{2})^{2} \cdot π = 16 \cdot r_{2}^{2} \cdot π = 16 \cdot A_{2}$ .
Ja, $k_{3}$ hat dann den 16-fachen Flächeninhalt von $k_{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründe die Behauptung mit der Formel für die Kreisfläche $A = π \cdot r^{2}$ .
Untersuche, was passiert, wenn der Radius vervierfacht wird (und anschließend quadriert wird).