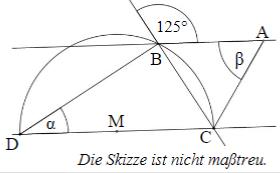
Die Punkte und liegen auf einer Kreislinie um den Mittelpunkt . Ermittle die fehlenden Winkelmaße und , wenn gilt: und .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Die Punkte und liegen auf einer Kreislinie um den Mittelpunkt . Ermittle die fehlenden Winkelmaße und , wenn gilt: und .
