2018
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
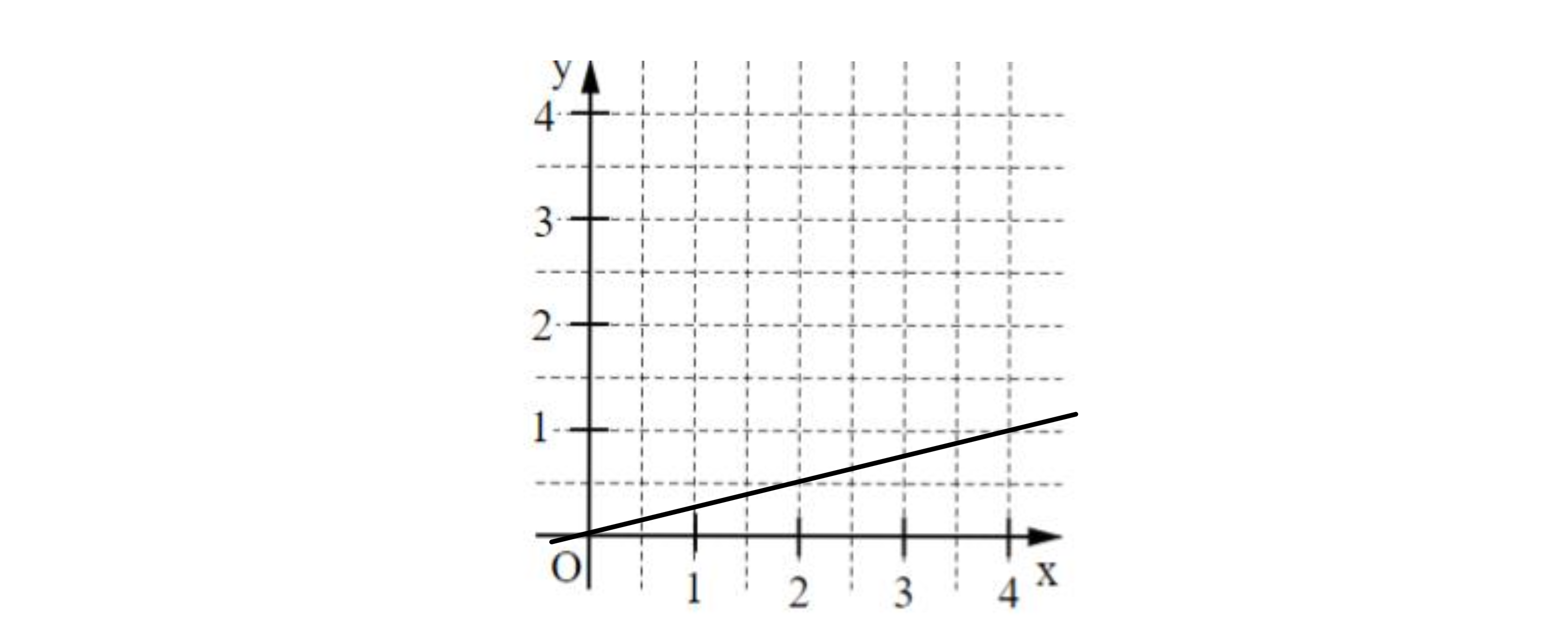
Gegeben ist ein Koordinatensystem.
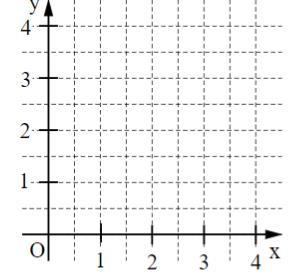
Zeichne die Gerade g mit der Gleichung in das Koordinatensystem ein
( x ). Achte auf Zeichengenauigkeit.
Die Gerade f verläuft parallel zur Geraden g aus Aufgabe a) (x). Schreibe den fehlenden Faktor in die Klammer, wenn für die Gleichung der Geraden f gilt:
( )
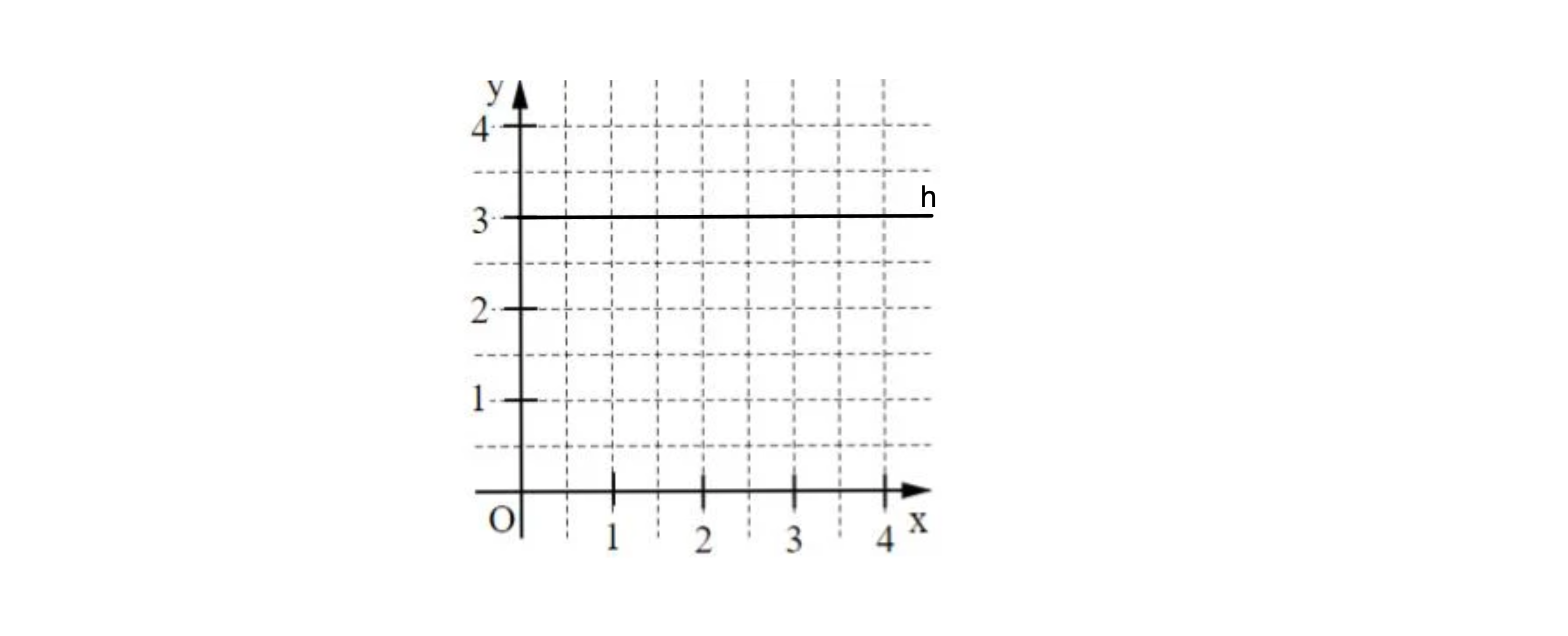
Gib die Gleichung einer Geraden h an, die die x-Achse nicht schneidet und einen positiven y-Achsenabschnitt hat (x).
- 2
Die Gerade g mit der Gleichung
, (x)
verläuft durch die Punkte und . Berechne die fehlende Koordinate des Punktes .
- 3
Bestimme die Lösungsmenge der Gleichung
()
- 4
Welche der folgenden Aussagen sind für jede beliebige Belegung von ( ) wahr? Kreuze die beiden wahren Aussagen an.
- 5
Setze so in die Lücken ein, dass äquivalente Terme entstehen ()

- 6
Leo hat für seine Familie Pfannkuchen gebacken. Er überlegt: „Wenn ich jedem Familienmitglied 2 Pfannkuchen gebe, bleiben 3 Stück übrig. Wenn ich aber jedem 3 Pfannkuchen geben möchte, dann habe ich 2 zu wenig. “Mit welcher Gleichung kann man die Anzahl () der Familienmitglieder rechnerisch bestimmen? Kreuze diese an.
- 7
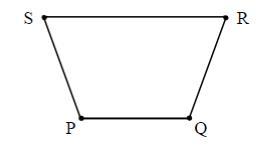
Für das gleichschenklige Trapez gilt:
Ergänze die Zeichnung zum gleichschenkligen Trapez .

- 8
Der Punkt ist der Mittelpunkt der Strecke mit ) und ). Gib die x-Koordinate des Punktes an.
A(_____|-15)
- 9
Bei einer Umfrage äußerte jeder fünfte Befragte, er sei mit seiner Berufswahl zufrieden. Das waren 80 Personen. 360 Personen gaben bei der gleichen Umfrage an, sie würden sich ein höheres Gehalt wünschen. Wie viel Prozent der Befragten wünschen sich ein höheres Gehalt?
- 10
Welche der folgenden quadratischen Terme haben für ein Maximum oder ein Minimum mit dem Wert 7?
Kreuze die beiden Terme an.
- 11
Welche Definitionsmenge passt zu den Bruchgleichungen?
- 12
Bestimme die Lösungsmenge der Bruchgleichung mit
, \ {-0,5}
- 13
Klammere beim folgenden Term den Faktor 0,5 aus.
- 14
Im Diagramm ist die Entwicklung der durchschnittlichen Gästezahlen eines Hotels in den Jahren 2000 bis 2015 dargestellt. Welche der folgenden Aussagen treffen für dieses Hotel zu?
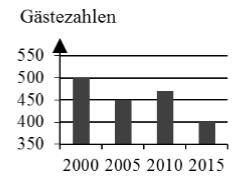
- 15
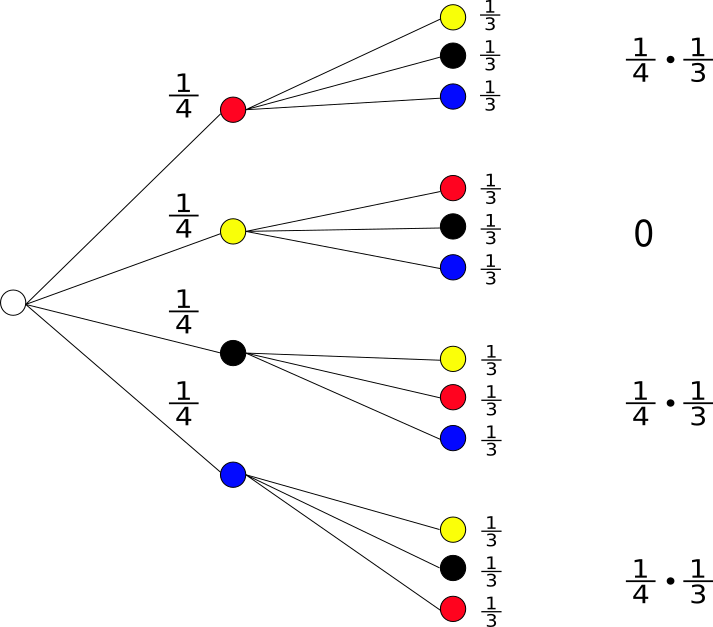
In einem blickdichten Säckchen befinden sich vier gleichartige Kugeln: eine rote, eine gelbe, eine schwarze und eine blaue Kugel. Dieter nimmt die vier Kugeln einzeln heraus, ohne sie jeweils zurückzulegen. Wie groß ist die Wahrscheinlichkeit, dass die gelbe Kugel als zweite gezogen wird?
- 16
Der Zug einer Achterbahn besteht aus lauter gleichen Waggons (siehe Abbildung). In jeder Reihe können zwei Personen nebeneinander sitzen. Ein Teil des Zuges wird durch ein Schild verdeckt.

Der Betreiber nahm insgesamt 210 € für eine Fahrt ein, bei der alle Plätze besetzt waren. Wie hoch ist der Fahrpreis pro Person?
€ - 17
Die Punkte und liegen auf einer Kreislinie um den Mittelpunkt . Ermittle die fehlenden Winkelmaße und , wenn gilt: und .
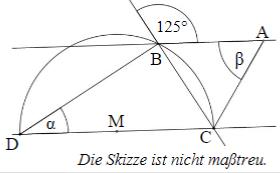
- 18
Das große Quadrat setzt sich aus 4 deckungsgleichen Rechtecken und einem kleinen Quadrat zusammen. Jedes Rechteck hat einen Umfang von 18 cm. Welchen Flächeninhalt hat das große Quadrat?
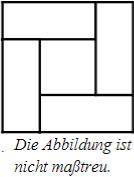 cm²
cm² - 19
Paula hat bei dem Dreieck die Maße , , ,
, und gemessen. Michaela schaut sich die Ergebnisse an und sagt: „So ein Dreieck kann es nicht geben. Da hast du bestimmt etwas falsch gemacht.“ Erkläre, wie sie ohne Zeichnung erkennen konnte, dass es ein solches Dreieck nicht geben kann.
- 20
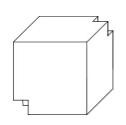
Aus einem Würfel mit der Kantenlänge wurden zwei kleinere Würfel mit jeweils einer Kantenlänge von ausgeschnitten (). Gib einen Term an, der das Volumen V des so entstandenen Körpers (siehe Abbildung) in Abhängigkeit von beschreibt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?