Zusammenfassen von Termen

Zusammenfassen von Summen

Hast du zum Beispiel den Term $x+x^2+x^3+2x^2+x^3$ gegeben, könnte man sich die Variable $x$ als eine Strecke der Länge $x$ vorstellen. $x^2$ wäre dann, wie der Name schon sagt, das Quadrat von $x$ und $x^3$ wiederum ein Würfel der Seitenlänge $x$.

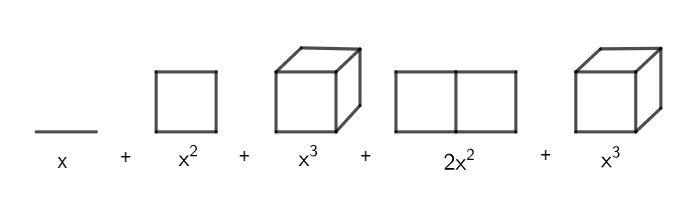
Du kannst sehen, dass du einen Strich nicht zu einem Quadrat hinzuzählen kannst. Du kannst nur die Quadrate und die Würfel zusammenzählen und erhältst insgesamt:

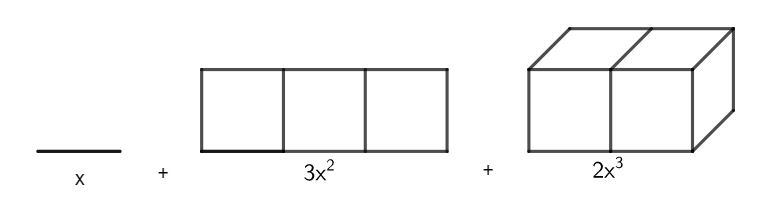
Die Rechnung ergibt:

Weiter kannst du sie nicht zusammenfassen!

Wenn du zwei verschiedene Variablen $x$ und $y$ in deinem Term hast, kannst du auch nur Teile mit den gleichen Variablen und jeweils gleichen Potenzen zusammenfassen!

Beispiel:

Hier kannst du nur die beiden Teile mit $xy$ zusammenfassen. Beachte, dass vor dem $2xy$ ein Minus als Vorzeichen steht!

Weiter kannst du auch diesen Term nicht zusammenfassen!

Es kann hilfreich sein, sich Teile des Terms mit gleichen Potenzen und Variablen in verschiedenen Farben zu markieren um den Term anschließend umzuformen.

Beispiel:

Zusammenfassen von Produkten

Bei Produkten können auch Teile mit unterschiedlichen Potenzen oder Variablen zusammengefasst werden.

Wenn du zum Beispiel den Term $2x \cdot 4xy$ zusammenfassen möchtest, kannst du auch schreiben:

umgestellt mithilfe des Kommutativgesetzes und der Potenzregeln erhältst du:

Beachte dabei unbedingt die Vorzeichen der Faktoren! Minus mal Minus ergibt Plus und Minus mal Plus ergibt Minus.

Beispiel:

Umstellen ergibt diesmal (das Minus bleibt bei einem der Faktoren aus der Klammer stehen):

Diesmal ergibt $2 \cdot (-7) \cdot (-3)$ eine positive Zahl, nämlich $42$. Der Term ist zusammengefasst: