In nachstehender Skizze gilt: ; ;
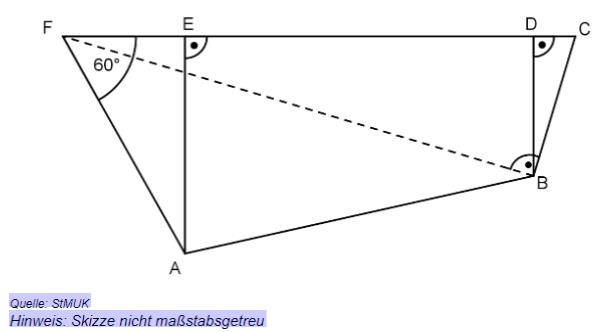
Berechnen Sie den Flächeninhalt des Trapezes ABDE.
In der oben abgebildeten Skizze lässt sich der Kathetensatz anwenden. Stellen Sie eine korrekte Anwendung dieses Satzes mit den entsprechenden Streckenbezeichnungen auf.
