Aufgabengruppe II
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
Lösen Sie die folgenden Aufgaben
Die Gerade hat die Funktionsgleichung . Berechnen Sie die Koordinaten des Schnittpunktes von mit der x-Achse und geben Sie an.
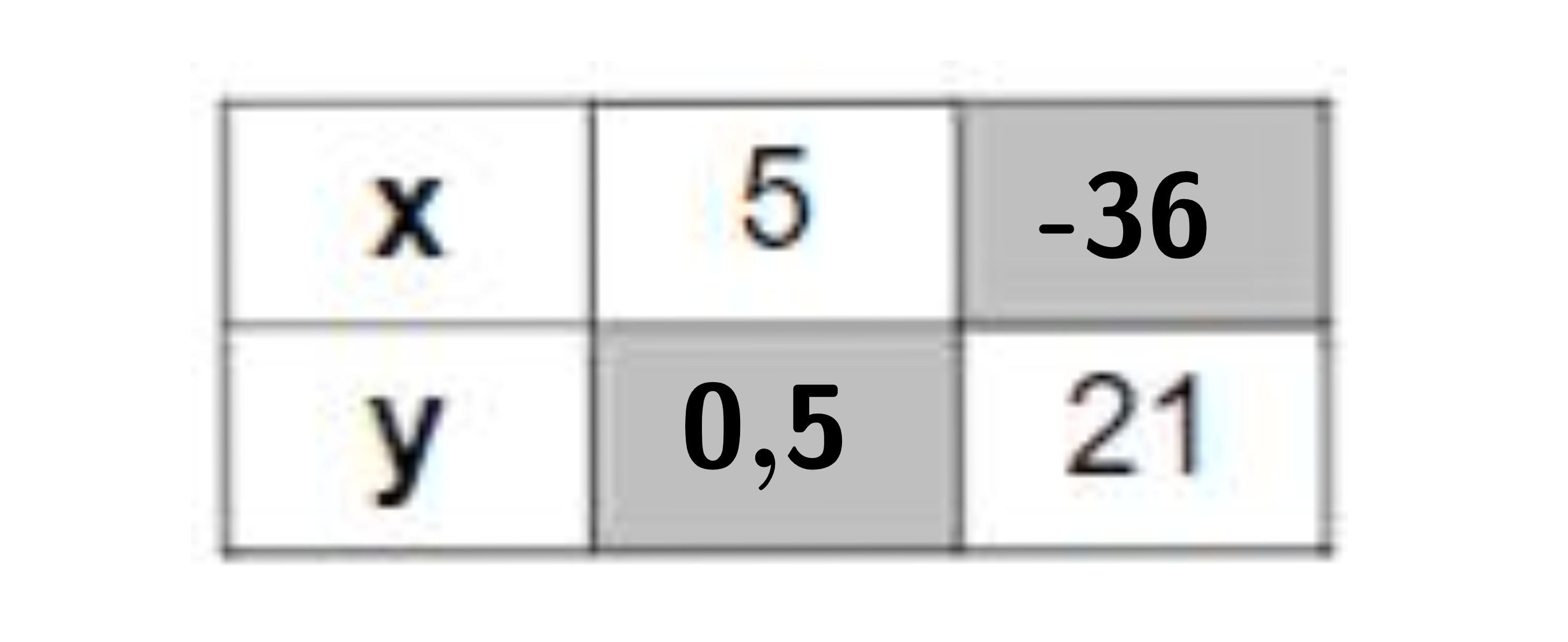
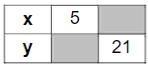
Übertragen Sie die Wertetabelle zur Geraden auf Ihr Lösungsblatt und ergänzen Sie die fehlenden Werte.
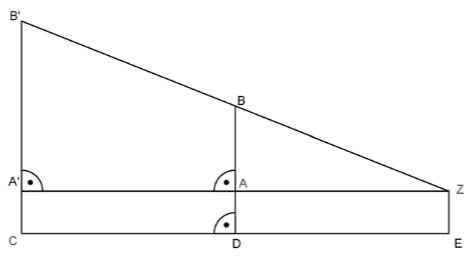
Die Gerade verläuft durch den Punkt und steht senkrecht auf der Geraden .
Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden .
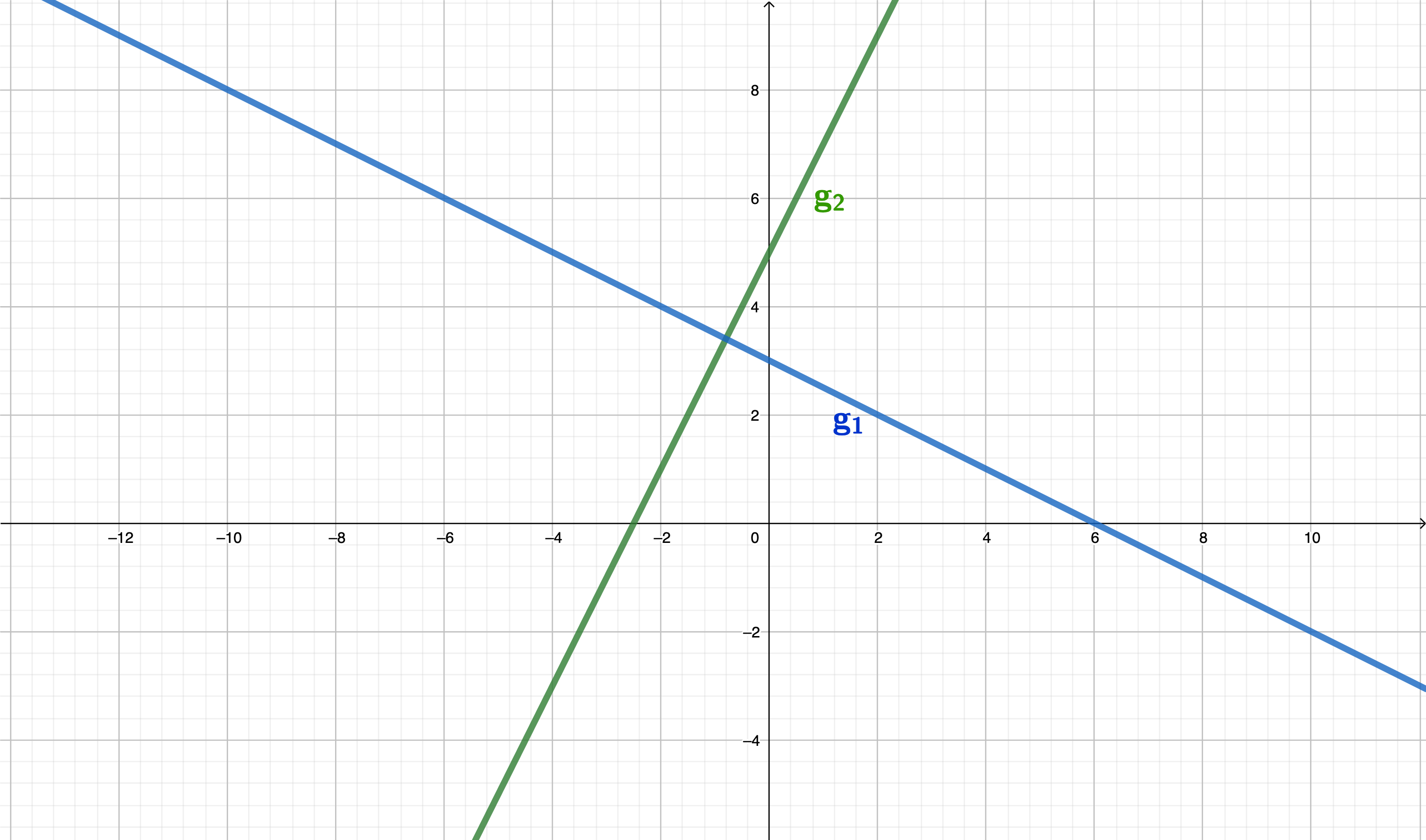
Zeichnen Sie die Geraden und in ein Koordinatensystem mit der Längeneinheit 1 cm.
Die Gerade verläuft durch die Punkte und . Ermitteln Sie die Funktionsgleichung von rechnerisch.
Die Gerade : schneidet die Gerade im Punkt . Bestimmen Sie durch Rechnung die Koordinaten dieses Schnittpunkts und geben Sie an
Gegeben ist der Graph der Funktion (siehe Zeichnung). Geben Sie die Funktionsgleichung der Geraden an.
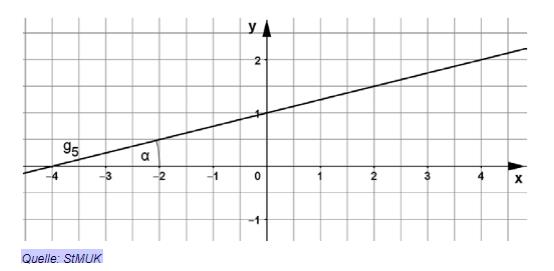
Berechnen Sie den Winkel α (siehe Zeichnung).
- 2
Lösen Sie die folgende Gleichung rechnerisch. Geben Sie die Definitionsmenge und die Lösungsmenge an.
- 3
Am 1. Januar 1998 hatte ein Sportverein in einer Großstadt 85000 Mitglieder.
Die Mitgliederzahl sank bis zum 1. Januar 2017 auf 63750 Mitglieder. Bestimmen Sie die durchschnittliche prozentuale Abnahme pro Jahr.
Am 1. Januar 2019 hatte der Verein 67800 Mitglieder. Die Vereinsführung erhoffte sich ab diesem Zeitpunkt ein jährliches Wachstum von 2,9 %. Berechnen Sie, nach wie vielen Jahren der Verein in diesem Fall wieder den Mitgliederstand vom 1. Januar 1998 erreichen würde. Runden Sie das Ergebnis auf volle Jahre.
JahreBerechnen Sie die Mitgliederzahl am 1. Januar 2030 im Falle einer gleichbleibenden jährlichen Steigerung um 3,3 % ab dem 1. Januar 2019.
- 4
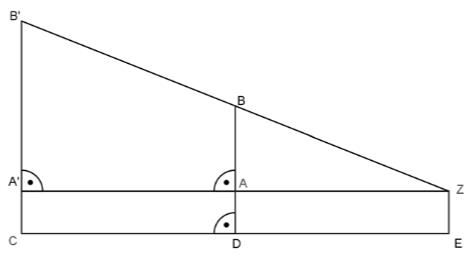
In nachstehender Skizze gilt: ; ;
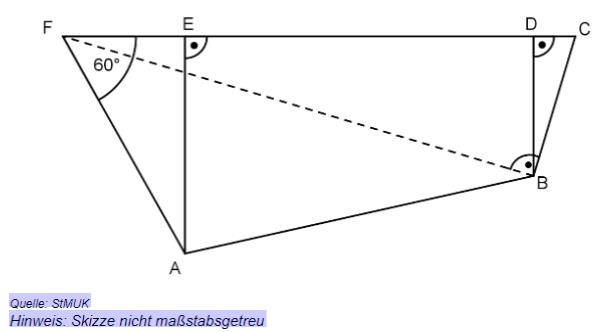
Berechnen Sie den Flächeninhalt des Trapezes ABDE.
In der oben abgebildeten Skizze lässt sich der Kathetensatz anwenden. Stellen Sie eine korrekte Anwendung dieses Satzes mit den entsprechenden Streckenbezeichnungen auf.
- 5
Lösen Sie die folgenden Aufgaben.
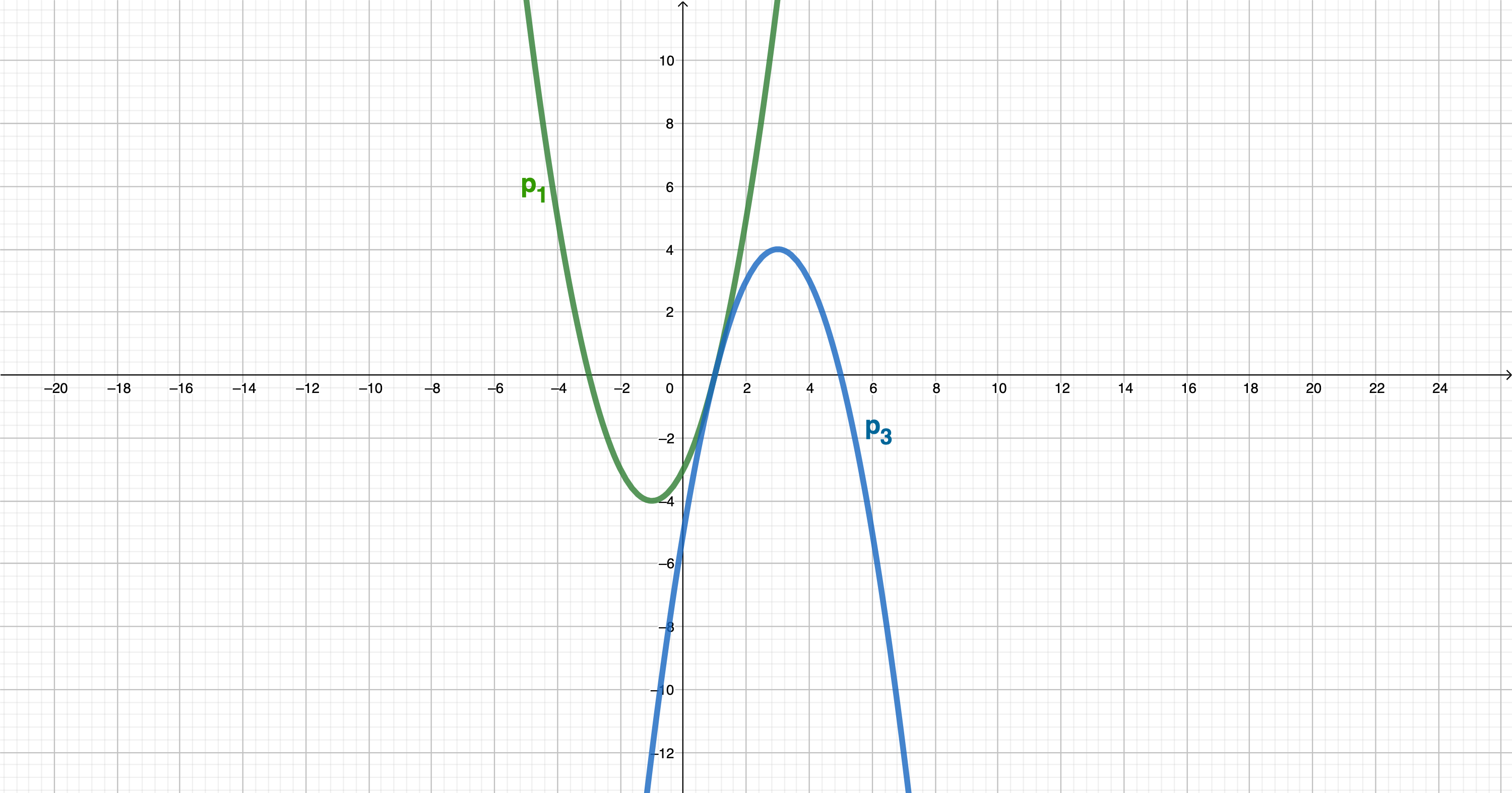
Eine nach oben geöffnete Normalparabel verläuft durch die Punkte und . Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Eine weitere Normalparabel hat die Funktionsgleichung . Bestimmen Sie rechnerisch die Scheitelpunktform und geben Sie den Scheitelpunkt an.
Die Normalparabel schneidet die x-Achse in den Punkten und .
Berechnen Sie die x-Koordinaten dieser Nullstellen.
Eine nach unten geöffnete Normalparabel hat den Scheitelpunkt Ermitteln Sie rechnerisch die Normalform der Funktionsgleichung von .
Zeichnen Sie die Normalparabeln und in ein Koordinatensystem mit der Längeneinheit 1cm.
Überprüfen Sie nachvollziehbar, ob folgende Aussage richtig oder falsch ist:
Der Punkt ist ein gemeinsamer Punkt der Normalparabel
: und der Geraden :
Die Normalparabel wird an der x-Achse gespiegelt. Geben Sie die Scheitelpunktform der so entstandenen Normalparabel an
- 6
Ersetzen Sie die Platzhalter in der folgenden Gleichung so, dass eine korrekte Anwendung einer binomischen Formel entsteht. Schreiben Sie die korrekte Gleichung vollständig auf Ihr Lösungsblatt.
Vereinfachen Sie die folgenden Terme so weit wie möglich. Es gilt: .
(I)
(II)
- 7
In folgender Skizze gilt: ; ; ; .
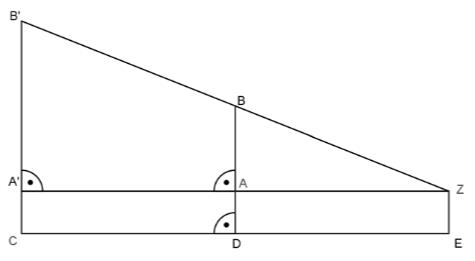
Quelle: StMUK
Hinweis: Skizze nicht maßstabsgetreu
Durch eine zentrische Streckung mit dem Zentrum wird die Strecke auf die Strecke abgebildet (siehe Skizze). Ermitteln Sie den Streckungsfaktor .
Berechnen Sie die Länge der Strecke ].
m
- 8
In einem Baumarkt gibt es unterschiedlich große Deko-Kugeln aus verschiedenen Materialien.
Bei einer Kugel mit dem Radius ist die untere Halbkugel geschliffen und poliert.
Berechnen Sie die Oberfläche der unteren Halbkugel.
Granit wiegt . Ermitteln Sie rechnerisch das Gewicht einer Granitkugel mit dem Durchmesser in Kilogramm.
Eine andere Deko-Kugel wird in einem mit Wasser gefüllten Zylinder aus Glas vollständig untergetaucht. Dieser Zylinder hat einen Durchmesser von . Der Wasserstand ist nach dem Eintauchen um höher. Berechnen Sie den Durchmesser dieser Deko-Kugel in .
- 9
Eine Lehrkraft bereitet für die Abschlussfeier äußerlich identische Glückskekse vor. davon enthalten je einen Wunsch für die Zukunft (W), zwölf enthalten ein jeweils unterschiedliches Sprichwort (S) und in den restlichen Keksen steckt jeweils ein Glückssymbol (G).
Alle Glückskekse befinden sich in einem Karton und sollen in zufälliger Reihenfolge einzeln herausgenommen werden. Berechnen Sie die Wahrscheinlichkeit, dass der erste herausgenommene Keks ein Glückssymbol enthält.
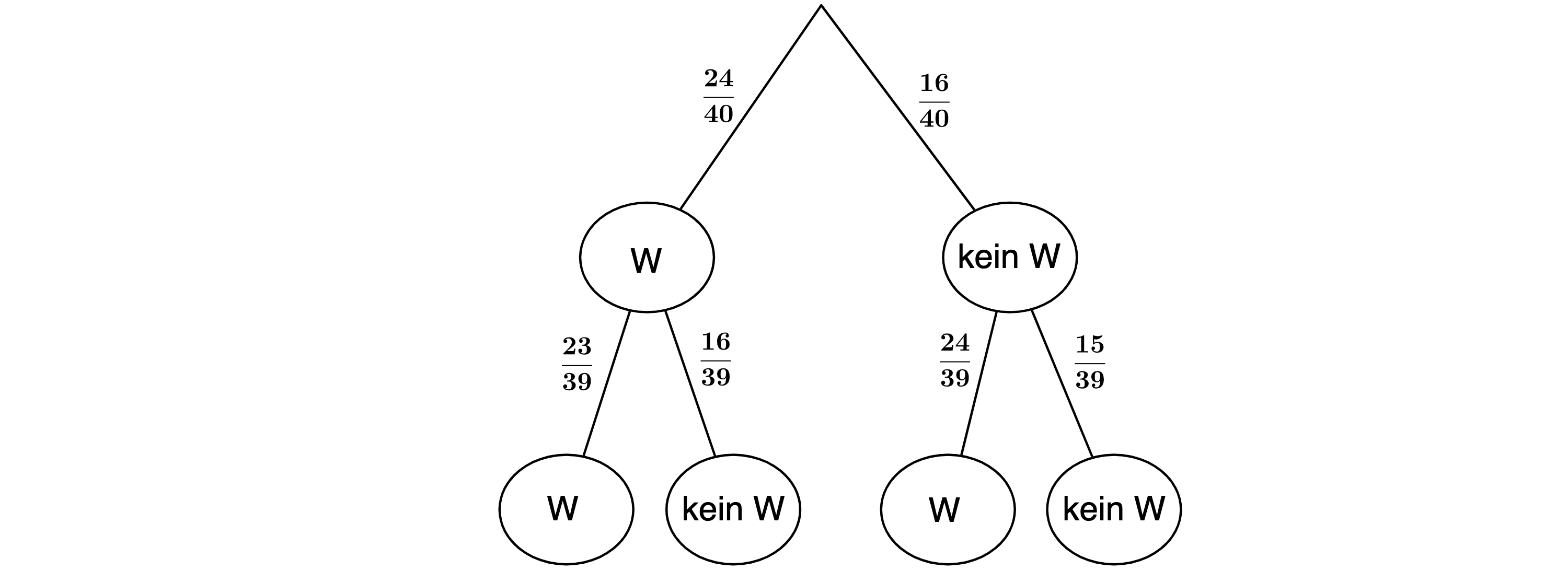
%Die Schülersprecherin darf als erste nacheinander zwei Kekse zufällig herausnehmen. Es wird nur zwischen den zwei Ereignissen „W“ und „kein W“ unterschieden. Erstellen Sie dazu ein Baumdiagramm. Beschriften Sie die Äste mit den jeweiligen Wahrscheinlichkeiten und berechnen Sie, mit welcher Wahrscheinlichkeit die Schülersprecherin mindestens ein „W“ zieht.
Nachdem alle Kekse entnommen worden sind, werden die zwölf Sprichwörter nun laut vorgelesen. Berechnen Sie die Anzahl aller möglichen Reihenfolgen, in denen die Sprichwörter vorgelesen werden können.
Möglichkeiten
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?